Додавання
Додава́ння — бінарна арифметична операція, суть якої полягає в об'єднанні математичних об'єктів.
| Результати обчислення | |
|---|---|
| Додавання (+) | |
| 1-й доданок + 2-й доданок = | сума |
| Віднімання (−) | |
| зменшуване − від'ємник = | різниця |
| Множення (×) | |
| 1-й множник × 2-й множник = | добуток |
| Ділення (÷) | |
| ділене ÷ дільник = | частка |
| Ділення з остачею (mod) | |
| ділене mod дільник = | остача |
| Піднесення до степеня | |
| основа степеняпоказник степеня = | степінь |
| Обчислення кореня (√) | |
| показник кореня √підкореневий вираз = | корінь |
| Логарифм (log) | |
| logоснова(число) = | логарифм |

Операцію додавання звичайно позначають знаком + (плюс). В окремих розділах математики додавання також позначається іншими специфічними для даної області символами ( тощо.)
Результатом додавання чисел і є число, яке називається сумою чисел і (доданків) і позначається [1]. Це одна з чотирьох елементарних арифметичних операцій, разом з відніманням, множенням і діленням. Додавання двох натуральних чисел є загальною сумою цих величин. Наприклад, комбінація з трьох і двох яблук (на малюнку) в сумі дає 5 яблук. Це спостереження еквівалентне алгебраїчному виразові «3 + 2 = 5», тобто, «3 плюс 2 дорівнює 5».
Операнди операції додавання називаються доданками, результат — сумою. Обернена до додавання операція називається відніманням.
Використовуючи систематичні узагальнення, додавання можна визначити для абстрактних величин, таких як цілі числа, раціональні числа, дійсні числа і комплексні числа, а також для інших абстрактних об'єктів, таких як вектори та матриці.
Додавання має кілька важливих властивостей (наприклад, для A — множини дійсних чисел) (див. Сума):
- Комутативність:
- Асоціативність:
- Дистрибутивність:
- У будь-якій непустій підмножині множини є тке число що усі відмінні від числа можна представити у вигляді де
- Додавання (нульового елементу) дає число, що дорівнює вихідному:
Ця система аксіом є категоричною - усі її моделі є ізоморфними. Наприклад, можна встановити ізоморфізм між звичайною інтерпретацією цієї системи аксіом, як множини із звичайною операцією додавання, і інтерпретацією у множині із операцією добутку. Для цього необхідно поставити у відповідність кожному натуральному числу число Тоді сумі відповідає число Оскільки то при відображенні операція додавання переходить у операцію добутку.
Додавання — одна з найпростіших задач з числами. Додавання дуже маленьких чисел зрозуміле навіть дітям. У початковій школі вчать рахувати в десятковій системі числення, починаючи зі складання простих чисел і поступово переходячи до складніших завдань. Відомі різні пристрої для додавання: від стародавніх абаків до сучасних комп'ютерів.
Форми запису і термінологія

Додавання записується з використанням знаку плюс «+» між складовими; така форма запису називається інфіксною нотацією. Результат записується з використанням знаку рівності. Наприклад,
- («один плюс один дорівнює два»)
- («два плюс два дорівнює чотири»)
- («три плюс три дорівнює шість»)
- (див. «асоціативність» нижче)
- (див. «множення» нижче)
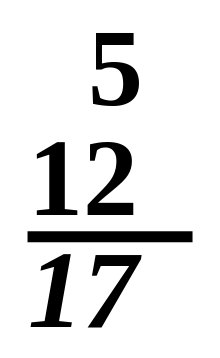
5 + 12 = 17
У деяких ситуаціях йдеться про додавання, але без використання символів додавання:
- Якщо є стовпчик чисел, останнє (нижнє) число в якому підкреслене, то зазвичай йдеться про те, що всі числа у стовпчику складаються, а одержана сума записується нижче підкресленого числа.
- Якщо перед дробом стоїть ціле число, то цей запис означає суму двох доданків — цілого числа і дробу, яку називають змішаним числом[2]. Наприклад,
3 = 3 + ½ = 3,5.
Такий запис може викликати плутанину, оскільки в більшості інших випадків, подібний запис означає множення, а не додавання[3].
Знак плюс «+» (Юнікод:U+002B; ASCII: +) — спрощення латинського слова «et», що означає «і», "та"[4]. Цей символ зустрічається в книгах, починаючи з 1489 року.[5]
Інтерпретації
Додавання використовують для моделювання безлічі фізичних процесів. Навіть для простого додавання натуральних чисел існує багато різних інтерпретацій і ще більше способів візуального представлення.
Комбінування наборів

Можливо, найбільш фундаментальна інтерпретація додавання — комбінування наборів:
- Якщо два або більше наборів об'єктів, що не перетинаються, об'єднані в один набір, то кількість об'єктів в отриманому наборі дорівнює сумі кількостей об'єктів у вихідних наборах.
Цю інтерпретацію легко унаочнити, при цьому небезпека двозначності буде мінімальною. Це також корисно у вищій математиці; строге визначення підсумовування дано нижче, див. Натуральні числа нижче. Однак не зрозуміло, як за допомогою цієї інтерпретації складання пояснити додавання дробових або від'ємних чисел[6].
Одним з можливих рішень буде використання набору об'єктів, які легко можна розділити, наприклад, пироги або ще краще — це стрижні з сегментами[7]. Замість комбінування наборів сегментів, стрижні можна приєднати один до одного кінцями, що ілюструє іншу концепцію складання: складаються не стрижні, а їх довжини.
Розширення довжини
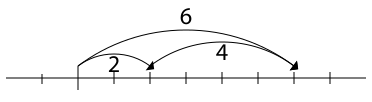

Друга інтерпретація додавання полягає в розширенні початкової довжини на величину доданої довжини:
- Коли початкова довжина розширюється на довжину, що додається, то отримана довжина дорівнює сумі початкової довжини та довжини, яку до неї додали[8].
Суму a + b можна інтерпретувати як бінарну операцію об'єднання a і b в алгебраїчному сенсі, також її можна інтерпретувати як додавання b одиниць до числа a. В останній інтерпретації частини суми a + b відіграють асиметричні ролі, і операція a + b розглядається як застосування до числа a унарної операції +b[9]. Унарний підхід дозволяє перейти до віднімання, адже кожна унарна операція додавання має зворотну унарну операцію віднімання і навпаки.
Загальні властивості операції додавання
Незалежно від природи математичних об'єктів, які можна додати, додавання характеризується властивостями, які наведені нижче. Будь-яку бінарну операцію, яка задовільняє зазначеним умовам у математиці можна назвати додаванням.
Комутативність

Додавання комутативне: від перестановки доданків сума не змінюється.. У символьному записі: якщо a і b — будь-які два числа, тоді
- a + b = b + a.
Комутативність додавання відома під назвою «комутативний закон додавання». Ця фраза означає, що є й інші закони комутативності: наприклад, існує комутативний закон множення. Втім, багато бінарних операцій, таких як віднімання і ділення, не комутативні, тому було б помилково говорити просто «комутативний закон».
Асоціативність
Додавання асоціативне: при складанні трьох або більше чисел черговість не має значення.
Наприклад, сума a + b + c означає (a + b) + c або a + (b + c)? Властивість асоціативності складання говорить нам, що вибір одного із запропонованих варіантів не має значення. Для будь-яких чисел a, b, і c справедлива рівність (a + b) + c = a + (b + c). Наприклад, (1 + 2) + 3 = 3 + 3 = 6 = 1 + 5 = 1 + (2 + 3).
Нейтральний елемент
Якщо додати нуль до будь-якого числа, то значення цього числа не зміниться; нуль — це нейтральний елемент для операції додавання. запис у вигляді символів: для будь-якого a,
- a + 0 = 0 + a = a.
Цей закон вперше описав Брамагупта 628 року у Виправленому трактаті Брахми. Він створив цей закон у вигляді трьох окремих законів: для негативного, позитивного та нульового числа a, і для опису цих законів він використовував слова, а не алгебраїчні символи. Пізніше індійські математики уточнили поняття; близько 840 року Махавіра написав, що «нуль стає таким самим, як те, що додається до нього», що відповідало запису 0 + a = a. У 12 столітті Бхаскара II написав: «Якщо додати нічого або відняти нічого, то кількість, позитивна чи негативна, залишається такою ж, як і була», що відповідає запису[10].
Наступне число
Додавання одиниці також відіграє особливу роль для цілих чисел: для будь-якого цілого числа a ціле число (a + 1) — це найменше число, на одиницю більше, ніж a, також відоме як наступне число за числом a[11]. Наприклад, 3 — це наступне число за числом 2, а 7 — це наступне число за числом 6. З урахуванням цієї наступності, значення «a» + «b» можна розглядати, як -те наступне за «а», таким чином, додавання можна визначити як ітеративне послідовне знаходження наступного числа. Наприклад, 6 + 2 буде 8, оскільки 8 йде після 7, яке йде після 6, отже, 8 — це друге наступне за 6.
Одиниці вимірювання
Щоб складати фізичні величини, їх значення привести до однакових одиниць вимірювання[12]. Наприклад, якщо скласти 50 мілілітрів і 150 мілілітрів, вийде 200 мілілітрів. Однак, якщо до 5 футів додати 2 дюйми, в сумі вийде 62 дюйми, тому що 60 дюймів це те ж саме, що і 5 футів. З іншого боку, зазвичай немає сенсу складати 3 метри і 4 квадратних метри, бо ці одиниці вимірювання неоднорідні; такі міркування є ключовими під час аналізу розмірності.
Виконання додавання
Вроджена здібність[13]
Дослідження розвитку математичних здібностей, які розпочалися в 1980-х роках, розглядали феномен звикання: немовлята довше дивляться на ситуації, які є для них несподіваними[14]. У своєму експерименті 1992 року Карен Вінн використовувала ляльки Міккі Мауса, з якими проводила різні маніпуляції за ширмою. Цей експеримент показав, що п'ятимісячні немовлята очікують, що 1 + 1 це 2, і дивуються, коли виявляється, що 1 + 1 це 1 або 3. Пізніше цей результат був підтверджений в інших лабораторіях з використанням різних методів[15]. В іншому експерименті 1992 року з малюками старшого віку, від 18 до 35 місяців, використовувався розвиток моторних функцій дітей, що дозволяло їм діставати кульки для настільного тенісу з коробки; наймолодші хлопці добре справлялися з невеликим числом кульок, а старші навчилися рахувати суму до 5[16].
Навіть деякі тварини демонструють здатність додавати, особливо примати. Експеримент 1995 року був аналогічний до експерименту Вінн 1992 року, але замість ляльок використовували баклажани. З'ясувалося, що макаки-резуси і едипові тамарини показують подібні до людських немовлят здібності. Ба більше, один шимпанзе, після того, як його навчили розрізняти і розуміти сенс арабських цифр від 0 до 4, зміг рахувати суму двох чисел без будь-якої підготовки[17]. Пізніше було з'ясовано, що індійські слони здатні оволодіти базовими арифметичними операціями[18].
Опанування додаванням дітьми
Зазвичай спочатку діти вчаться лічби. Якщо дати завдання, в якому потрібно об'єднати два предмети і три предмети, маленькі діти моделюють ситуацію за допомогою конкретних предметів, наприклад, лічать на пальцях або малюють. У міру набуття досвіду, вони вчать або відкривають для себе стратегію «підрахунку»: коли потрібно знайти, скільки буде два плюс три, то діти перелічують два числа, що йдуть після числа три, промовляючи: «три, чотири, п'ять» (зазвичай загинаючи пальці), і, в підсумку, отримуючи п'ять. Ця стратегія здається майже універсальною; діти можуть легко перейняти її у однолітків або вчителів[19]. Більшість дітей самі доходять до цього. Маючи якийсь досвід, діти вчаться складати швидше, використовуючи комутативність додавання, починаючи перераховувати числа від найбільшого числа в сумі, як в описаному вище випадку, починаючи з трьох і перелічуючи: «чотири, п'ять». Зрештою, діти починають використовувати будь-які факти про складення (приклади додавання напам'ять), отримуючи їх або шляхом досвіду, або запам'ятовуючи їх. Коли одні факти осядуть в пам'яті, діти починають виводити невідомі факти з відомих. Наприклад, дитина, яка складає шість і сім, може знати, що 6 + 6 = 12, і тому 6 + 7 на один більше, тобто 13[20]. До такого способу виведення приходять досить швидко і більшість учнів початкової школи покладаються на суміш всього того, що вони запам'ятали і того, що вони можуть вивести, що в підсумку дозволяє їм швидко складати[21].
У різних країнах до вивчення цілих чисел і арифметики приступають у різному віці, переважно додавання вчать у закладах дошкільної освіти[22]. При цьому у всьому світі до кінця першого року початкової школи школярі навчаються додавання[23].
Таблиця додавання
Дітям часто показують таблицю додавання пар чисел від 1 до 10 для кращого запам'ятовування. Знаючи цю таблицю, можна виконати будь-яке додавання.
| 1+ | 2+ | 3+ | 4+ | 5+ | 6+ | 7+ | 8+ | 9+ | 10+ |
|---|---|---|---|---|---|---|---|---|---|
| 1 + 0 = 1 | 2 + 0 = 2 | 3 + 0 = 3 | 4 + 0 = 4 | 5 + 0 = 5 | 6 + 0 = 6 | 7 + 0 = 7 | 8 + 0 = 8 | 9 + 0 = 9 | 10 + 0 = 10 |
| 1 + 1 = 2 | 2 + 1 = 3 | 3 + 1 = 4 | 4 + 1 = 5 | 5 + 1 = 6 | 6 + 1 = 7 | 7 + 1 = 8 | 8 + 1 = 9 | 9 + 1 = 10 | 10 + 1 = 11 |
| 1 + 2 = 3 | 2 + 2 = 4 | 3 + 2 = 5 | 4 + 2 = 6 | 5 + 2 = 7 | 6 + 2 = 8 | 7 + 2 = 9 | 8 + 2 = 10 | 9 + 2 = 11 | 10 + 2 = 12 |
| 1 + 3 = 4 | 2 + 3 = 5 | 3 + 3 = 6 | 4 + 3 = 7 | 5 + 3 = 8 | 6 + 3 = 9 | 7 + 3 = 10 | 8 + 3 = 11 | 9 + 3 = 12 | 10 + 3 = 13 |
| 1 + 4 = 5 | 2 + 4 = 6 | 3 + 4 = 7 | 4 + 4 = 8 | 5 + 4 = 9 | 6 + 4 = 10 | 7 + 4 = 11 | 8 + 4 = 12 | 9 + 4 = 13 | 10 + 4 = 14 |
| 1 + 5 = 6 | 2 + 5 = 7 | 3 + 5 = 8 | 4 + 5 = 9 | 5 + 5 = 10 | 6 + 5 = 11 | 7 + 5 = 12 | 8 + 5 = 13 | 9 + 5 = 14 | 10 + 5 = 15 |
| 1 + 6 = 7 | 2 + 6 = 8 | 3 + 6 = 9 | 4 + 6 = 10 | 5 + 6 = 11 | 6 + 6 = 12 | 7 + 6 = 13 | 8 + 6 = 14 | 9 + 6 = 15 | 10 + 6 = 16 |
| 1 + 7 = 8 | 2 + 7 = 9 | 3 + 7 = 10 | 4 + 7 = 11 | 5 + 7 = 12 | 6 + 7 = 13 | 7 + 7 = 14 | 8 + 7 = 15 | 9 + 7 = 16 | 10 + 7 = 17 |
| 1 + 8 = 9 | 2 + 8 = 10 | 3 + 8 = 11 | 4 + 8 = 12 | 5 + 8 = 13 | 6 + 8 = 14 | 7 + 8 = 15 | 8 + 8 = 16 | 9 + 8 = 17 | 10 + 8 = 18 |
| 1 + 9 = 10 | 2 + 9 = 11 | 3 + 9 = 12 | 4 + 9 = 13 | 5 + 9 = 14 | 6 + 9 = 15 | 7 + 9 = 16 | 8 + 9 = 17 | 9 + 9 = 18 | 10 + 9 = 19 |
| 1 + 10 = 11 | 2 + 10 = 12 | 3 + 10 = 13 | 4 + 10 = 14 | 5 + 10 = 15 | 6 + 10 = 16 | 7 + 10 = 17 | 8 + 10 = 18 | 9 + 10 = 19 | 10 + 10 = 20 |
Десяткова система
Для успішного додавання в десятковій системі потрібно пам'ятати або вміти швидко виводити 100 «фактів (прикладів) додавання» для однорозрядних чисел. Хтось може запам'ятати всі ці факти, заучуючи їх, але стратегії вивчення додавання шляхом використання шаблонів більш інформативні і для більшості людей більш ефективні:[24]
- Комутативна властивість: використання шаблону a + b = b + a знижує кількість «фактів про складання», які потрібно запам'ятати, зі 100 до 55.
- На один або на два більше: додавання 1 або 2 — це базова задача, і розв'язати її можна переліченням (підрахунком) або, зрештою, покладаючись на інтуїцію[24].
- Нуль: оскільки нуль є нейтральним елементом для операції додавання (адитивною одиницею), то додати нуль просто. Втім, під час вивчення арифметики деяким учням додавання здається процесом, у якому складові завжди збільшуються; акцент на словесному формулюванні задачі може допомогти зрозуміти «винятковість» нуля[24].
- Подвоєння: складання числа з самим собою пов'язане із задачею подвоєного (повторного) підрахунку і множенням. Факти про подвоєння є основою для багатьох пов'язаних з ними фактів, і учням їх відносно легко збагнути[24].
- Майже-подвоєння (суми, наближені до операції подвоєння): суму 6 + 7 = 13 можна швидко вивести з факту про подвоєння 6 + 6 = 12 і додавання одиниці, або факту 7 + 7 = 14 і віднімання одиниці[24].
- П'ять і десять: суми, які мають вигляд 5 + x і 10 + x, зазвичай запам'ятовуються рано і можуть бути використані для виведення інших фактів. Наприклад, результат суми 6 + 7 = 13 можна вивести з використання факту 5 + 7 = 12 додавши до цього одиницю[24].
- Добування десятки (добудовування до десяти): існує така стратегія, в якій 10 використовують як проміжний результат за наявності доданків 8 чи 9; наприклад, 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14[24].
У міру дорослішання учні запам'ятовують все більше фактів, і вчаться швидко виводити з них інші факти. Багато учнів не запам'ятовують усі факти, але можуть швидко вивести потрібний[21].
Перенесення
У стандартному алгоритмі додавання багаторозрядних чисел цифри, з яких складаються записи чисел, що додаються, розташовані одна під одною. Виконують додавання цифр окремо в кожному стовпчику, починаючи з правого. Якщо сума цифр у стовпчику перевищує 10, зайву цифру «переносять» у наступний стовпчик (лівіше). Наприклад, у сумі 27 + 59
¹ 27 + 59 ———— 86
7 + 9 = 16 і цифра 1 переноситься в наступний стовпчик. В альтернативному способі починають додавання з найбільш значущої цифри ліворуч; у цій стратегії перенесення виконується дещо грубіше, але швидше виходить приблизна сума. Існує багато інших методів переносу.
Додавання десяткових дробів
Спосіб додавання десяткових дробів є простою модифікацією додавання багаторозрядних чисел, описаного вище[25]. При додаванні в стовпчик дроби розташовують таким чином, щоб коми перебували точно одна під одною. За необхідності, можна додавати нулі справа і зліва до більш короткого дробу (див. нуль, що замикає і провідні нулі), щоб зробити її завдовжки рівною довшому дробові. Отже, додавання проводять так само, як і в описаному вище способі додавання багаторозрядних чисел, тільки кому розташовують у відповіді точно там само, де її розташовують у доданках.
Наприклад, суму 45,1 + 4,34 можна обчислити таким чином:
4 5 , 1 0 + 0 4 , 3 4 ------------ 4 9 , 4 4
Експоненціальний запис
В експоненціальному записі числа записують у вигляді , де — мантиса і — характеристика числа. Щоб скласти два числа, які записані в експоненціальній формі, потрібно, щоб вони мали однакові характеристики.
Наприклад:
Додавання в інших системах числення
Додавання для чисел з іншими основами дуже нагадує додавання в десятковій системі. Як приклад можна розглянути додавання у двійковій системі числення[26]. Додавання двох однорозрядних двійкових чисел з використанням перенесенням є доволі простим:
- 0 + 0 → 0
- 0 + 1 → 1
- 1 + 0 → 1
- 1 + 1 → 0, переноситься 1 (оскільки 1 + 1 = 2 = 0 + (1 × 21))
Сума двох знаків «1» дорівнює знакові «0», а 1 потрібно додати до наступного стовпчика. Ця ситуація аналогічна до того, що відбувається в додатковій системі при додаванні певних однохначних чисел; якщо результат дорівнює або перевищує значення основи системи числення (10), то цифри зліва збільшуються:
- 5 + 5 → 0, перенесення 1 (оскільки 5 + 5 = 10 = 0 + (1 × 101))
- 7 + 9 → 6, перенесення 1 (оскільки 7 + 9 = 16 = 6 + (1 × 101))
Ця операція відома під назвою «перенесення»[27]. Коли результат додавання перевершує діапазон значень і розряду, то потрібно «перенести» надлишок, поділений на основу системи (тобто на 10 у десятковій системі) вліво, додаючи його до значення в наступному розряді. Це пов'язано з тим, що значення в наступному розряді в разів більше (у -ій системі числення), ніж значення в поточному розряді. Перенесення в двійковій системі числення працює так само, як і в десятковій системі:
1 1 1 1 1 (перенесення)
0 1 1 0 1
+ 1 0 1 1 1
—————————————
1 0 0 1 0 0 = 36
У цьому прикладі додаються два числа: 011012 (1310) і 101112 (2310). У верхньому рядку вказано наявність переносу. Починаємо складати з правого стовпчика: 1 + 1 = 102. Тут 1 переноситься вліво, а 0 записується в нижньому рядку. Тепер складаються числа у другому стовпчику праворуч: 1 + 0 + 1 = 102; 1 переноситься, а 0 записується в нижньому рядку. Третій стовпчик: 1 + 1 + 1 = 112. В цьому випадку 1 переноситься в нижньому рядку. У підсумку отримуємо 1001002 (або 36 в десятковій системі числення).
Комп'ютери
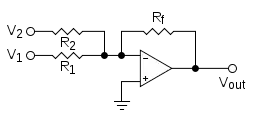
Аналогові комп'ютери працюють безпосередньо з фізичними величинами, тому їх механізм складання залежить від виду доданків. Механічний інтегратор може представляти два доданки у вигляді позицій ковзних блоків, в цьому випадку їх можна складати за допомогою усереднювального важеля. Якщо доданки представлені у вигляді швидкостей обертання двох валів, то їх можна скласти за допомогою диференціалу. Гідравлічний суматор може додавати тиски у двох камерах, використовуючи другий закон Ньютона, щоб врівноважити сили на збірку поршнів. Найтиповіший випадок застосування аналогового комп'ютера — це додавання двох напруг (відносно заземлення); це можна грубо реалізувати за допомогою схеми з резисторами, а у вдосконаленій версії використовується операційний підсилювач[28].
Операція додавання є базовою у персональному комп'ютері. Продуктивність операції додавання і особливо обмеження, пов'язані з механізмом перенесення, впливають на загальну продуктивність комп'ютера.

Абак, який також називають рахівницею — це обчислювальний прилад, який використовували за багато століть до прийняття сучасної системи числення, і який все ще широко застосовують купці, торговці та клерки в Азії, Африці та на інших континентах; передбачають, що абак створений не пізніше 2700-2300 до н. е., тоді його використовували шумери[29].
1642 року Блез Паскаль винайшов механічний калькулятор, під назвою Паскаліна[30][31]; це була перша операційна сумувальна машина. У цьому калькуляторі механізм перенесення здійснювався завдяки гравітації. Це був єдиний операційний калькулятор у 17 столітті і найперший автоматичний цифровий комп'ютер. Паскаліна була обмежена своїм механізмом переносу, який дозволяв крутити колеса лише в один бік і, таким чином, додавати. Щоб відняти, користувачеві потрібно було використати другий набір цифр, для представлення результату, та методи доповнення, які містили таку саму кількість кроків, що й додавання. Джованні де Полені продовжив справу Паскаля, побудувавши другий функціональний механічний калькулятор у 1709 році. Циферблат цього калькулятора був з дерева, і, одного разу встановлений, він міг перемножувати два числа між собою автоматично.

Суматорb виконують цілочисельне додавання в електронних цифрових обчислювальних машинах, зазвичай використовуючи бінарну арифметику. В найпростішій структурі використовується суматор хвильового переносу (англ. Ripple-carry adder) (вихідне перенесення попереднього в ланцюжку суматора є вхідним перенесенням для наступного суматора), це дозволяє виконувати додавання для багаторозрядних чисел. Невелике поліпшення представлено в суматорі з пропуском перенесення, який діє подібним до людської інтуїції чином; він не виконує всі перенесення в сумі 999 + 1, а обходить групу дев'яток і перескакує одразу до відповіді[32].
На практиці додавання можна виконувати через додавання по модулю два і операцію «І» в поєднанні з іншими бітовими операціями, як показано нижче. Обидві ці операції просто реалізувати в ланцюгах суматорів, які, в свою чергу, можна об'єднувати в складніші логічні операції. У сучасних цифрових комп'ютерах додавання цілих чисел є найшвидшою операцією, водночас воно має величезний вплив на загальну продуктивність комп'ютера, оскільки ціле додавання лежить в основі всіх операцій з рухомою комою, а також в таких завданнях, як генерація адрес під час доступу до пам'яті і вибірка команд під час визначеного порядку їх виконання. Щоб збільшити швидкість, сучасні комп'ютери обчислюють значення в разрядах паралельно; такі схеми називаються вибірка перенесення, передбачення перенесення і псевдоперенесення у суматорі Лінга. У більшості випадків реалізація додавання на комп'ютері є гібридом останніх трьох конструкцій[33][34]. На відміну від паперу, додавання на комп'ютері часто змінює доданки. На стародавньому абаці та рахівниці під час виконання операції додавання обидва доданки знищувалися, залишалася лише сума. Вплив абака на математичне мислення був настільки великим, що в ранніх латинських текстах часто стверджувалося, що в процесі складання «числа з числом» обидва числа зникають[35]. Повертаючись до сучасності, зазначимо, що інструкція ADD мікропроцесора замінює значення першого доданку сумою, другий доданок залишається без змін[36]. У мові програмування високого рівня оцінювання a + b не змінює ні a, ні b; якщо ставиться завдання записати суму в a, то це потрібно явно вказати, зазвичай з виразом a = a + b. У деяких мовах програмування, таких як C або C++ цей запис скорочується до a += b.
// Iterative Algorithm
int add(int x, int y){
int carry = 0;
while (y != 0){
carry = AND(x, y); // Logical AND
x = XOR(x, y); // Logical XOR
y = carry << 1; // left bitshift carry by one
}
return x;
}
// Recursive Algorithm
int add(int x, int y){
return x if (y == 0) else add(XOR(x, y) , AND(x, y) << 1);
}
Якщо результат додавання занадто великий, то на комп'ютері відбувається арифметичне переповнення, яке призводить до неправильного результату. Непередбачуване арифметичне переповнення є доволі поширеною причиною програмних помилок. Такі помилки не завжди легко виявити і діагностувати, оскільки вони можуть проявитися при дуже великих вхідних наборах даних, які не часто застосовують у тестах[37].
Визначення для конкретних множин
Додавання натуральних чисел
Є два популярних способи визначення суми двох натуральних чисел a і b. Якщо натуральні числа визначають через потужність множини з кінцевою кількістю елементів, тоді доцільно дати таке визначення суми:
- Нехай N(S) — потужність множини S. Візьмемо дві множини A і B, що не перетинаються, причому N(A) = a і N(B) = b. Тоді a + b можна визначити як: [38][39][40].
Тут, — це об'єднання множин A і B. В альтернативній версії цього визначення множини A і B перекриваються і тоді за суму беруть їх диз'юнктне об'єднання, механізм, який дозволяє відокремлювати загальні елементи, внаслідок чого ці елементи враховуються двічі.
Інше відоме визначення рекурсивне:
- Нехай n+ — наступне за n натуральне число, наприклад 0+=1, 1+=2. Нехай a + 0 = a. Тоді загальна сума визначається рекурсивно: a + (b+) = (a + b)+. Звідси 1 + 1 = 1 + 0+ = (1 + 0)+ = 1+ = 2[41]>.
В аксіоматиці Пеано вся арифметика побудована на додаванні одиниці, тобто наступного числа.
Щоб до натурального числа додати натуральне число потрібно збільшити число на одиницю разів.
Наприклад,
- 5 + 4 = 5 + 1 + 1 + 1 + 1 = 6 + 1 + 1 + 1 = 7 + 1 + 1 = 8 + 1 = 9
Додавання цілих чисел
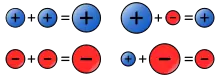
Найпростіша концепція цілого числа полягає в тому, що ціле число складається з його абсолютної величини і знака (зазвичай, число є додатним або від'ємним). У множині цілих чисел існує число 0 (нуль) — це особливий випадок: нуль не є ані додатним, ані від'ємним числом. Додавання його до будь-якого іншого цілого числа не змінює цього числа. Відповідне визначення додавання має враховувати такі випадки:
- Нехай n — ціле число і |n| - його абсолютне значення. Нехай a та b — цілі числа. Якщо яке-небудь з чисел a або b дорівнює нулю, то вважаємо таке число нейтральним елементом (адитивною одиницею). Якщо a і b обидва додатні, тоді припустимо a + b = |a| + |b|. Додавання додатних цілих чисел аналогічне додаванню натуральних чисел. Якщо a і b обидва від'ємні, тоді a + b = −(|a|+|b|). Якщо a і b мають різні знаки, то a + b — це різниця між |a| і |b|, і знак перед цією різницею ставиться такий, який стояв перед доданком з найбільшим абсолютним значенням[42][43]. Наприклад, розглянемо суму: -6 + 4 = -2; оскільки у чисел -6 і 4 різні знаки, то їх абсолютні значення віднімаються, і оскільки абсолютне значення від'ємного числа тут більше, ніж абсолютне значення додатного, то відповідь буде від'ємною.
Хоча це визначення може бути корисним для конкретних завдань, досить важко робити якісь загальні докази, оскільки потрібно розглядати дуже багато випадків.
Набагато зручнішою концепцією цілих чисел є побудова груп Гротендіка. Головна ідея полягає в тому, що кожне ціле число можна представити (не одним способом) як різницю двох натуральних чисел, тому ми можемо визначити ціле число, як різницю двох натуральних чисел. Тоді додавання визначається наступним чином через віднімання:
- Нехай є два цілих числа a − b і c − d, де a, b, c і d — натуральні числа, тоді (a − b) + (c − d) = (a + c) − (b + d)[44].
Якщо другий доданок від'ємний, то для отримання суми потрібно зменшити перший доданок на відповідну кількість одиниць.
Наприклад,
- 5 + (-4) = 5 + (-1) + (-1) + (-1) + (-1) = 4 + (-1) + (-1) + (-1) = 3 + (-1) + (-1) = 2 + (-1) = 1
Додавання раціональних чисел
Для додавання раціональних чисел необхідно привести їх до спільного знаменника, а потім додати чисельники, взявши спільний знаменник за знаменник суми:
- Припустимо
Наприклад,
- .
Додавання дробів з однаковими знаменниками набагато простіше; в цьому випадку можна просто скласти чисельники, залишивши знаменник без зміни: наприклад [45].
Комутативність і асоціативність додавання раціональних чисел є наслідком законів цілочисельної арифметики[46]. Більш строге і загальне визначення (див. у статті поле дробів).
Додавання ірраціональних чисел
Кожне ірраціональне число є границею певної послідовності раціональних наближень. Якщо ірраціональне число , а ірраціональне число , то
Додавання векторів
Для додавання векторів, визначених у векторному просторі з базисом потрібно додати їхні компоненти
Додавання матриць
Додавати можна матриці, які мають однакове число рядків і стовпчиків. Сума таких матриць має теж саме число рядків і стовпчиків, а кожен елемент матриці суми є сумою елементів матриць-доданків. Наприклад,
Додавання множин
Для множин операція об'єднання задовольнає вимогам комутативності і асоціативності, а тому є аналогом додавання.
Додавання елементів груп
В загальному випадку групові операції не мають властивості комутативності. Групи, для яких групова операція комутативна, називаються абелевими. Якщо групову операцію абелевої групи позначають плюсом, то таку групу називають адитивною.
Додавання в математичній логіці
В математичній логіці додаванню відповідає операція АБО. Результат цієї операції ІСТИНА якщо хоча б один із операндів має значення ІСТИНА.
Операція додавання в булевій алгебрі позначається символом .
Логіка
У логіці додаванням називають коректну, просту форма аргументації:
- A, отже, A або B.
або у логіко-операторній нотації:
- .
Аргумент має одне вихідне припущення A. Із істинності A слідує що A або B є істиною.
Приклад аргументу у формі додавання:
- Демократія є найкращою формою управління.
- Отже, демократія є найкращою формою управління, або кожен повинен голосувати.
Примітки
- Математический энциклопедический словарь, 1988, с. 546.
- Devine et al. p.263
- Mazur, Joseph. Enlightening Symbols: A Short History of Mathematical Notation and Its Hidden Powers. Princeton University Press, 2014. p. 161
- Cajori, Florian (1928). Origin and meanings of the signs + and -. A History of Mathematical Notations, Vol. 1. The Open Court Company, Publishers.
- plus. Оксфордський словник англійської мови (вид. 3-тє) (Oxford University Press). Вересень 2005. (Необхідна підписка або членство у публічній бібліотеці Сполученого Королівства .)
- See Viro 2001 for an example of the sophistication involved in adding with sets of "fractional cardinality".
- Кілпатрік, 2001.
- Mosley, F. (2001). Using number lines with 5-8 year olds. Nelson Thornes. p.8
- Li, Y., & Lappan, G. (2014). Mathematics curriculum in school education. Springer. p. 204
- Kaplan pp.69–71
- Hempel, C. G. (2001). The philosophy of Carl G. Hempel: studies in science, explanation, and rationality. p. 7
- R. Fierro (2012) Mathematics for Elementary School Teachers. Cengage Learning. Sec 2.3
- Александров П.С., Маркушевич А.И., Хинчин А.Я. - Энциклопедия элементарной математики, книга 1, с. 15-79.
- Wynn p.5
- Wynn p.15
- Wynn p.17
- Wynn p.19
- Randerson, James (21 August 2008). Elephants have a head for figures. The Guardian. Процитовано 29 March 2015.
- F. Smith p.130
- Carpenter, Thomas; Fennema, Elizabeth; Franke, Megan Loef; Levi, Linda; Empson, Susan (1999). Children's mathematics: Cognitively guided instruction. Portsmouth, NH: Heinemann. ISBN 0-325-00137-5.
- Henry, Valerie J.; Brown, Richard S. (2008). First-grade basic facts: An investigation into teaching and learning of an accelerated, high-demand memorization standard. Journal for Research in Mathematics Education 39 (2): 153–183. doi:10.2307/30034895.
- Beckmann, S. (2014). The twenty-third ICMI study: primary mathematics study on whole numbers. International Journal of STEM Education, 1(1), 1-8. Chicago
- Schmidt, W., Houang, R., & Cogan, L. (2002). A coherent curriculum. American educator, 26(2), 1-18.
- Fosnot and Dolk p. 99
- Rebecca Wingard-Nelson (2014) Decimals and Fractions: It's Easy Enslow Publishers, Inc.
- Дейл, 2008, с. 155.
- Ботман, 1837, с. 31.
- Трайт і Рождерс, 1960, с. 41-49.
- Джорджс, 2001, с. 11.
- Маргун, 1994, с. 48.
- Танон, 1963, с. 62.
- Флінн і Оверман, 2001, с. 2—8.
- Флінн і Оверман, 2001, с. 1—9.
- Санг-Су Йо, 2010, с. 194.
- Карпінскі, 1925, с. 102—103.
- Хоровець і Гілл, 2009, с. 679.
- Блотч, 2006, с. 1.
- Бегл, 1975, с. 49.
- Джонсон, 1975, с. 120.
- Девайн і співавтори, 1991, с. 75.
- Ендертон, 1977, с. 79.
- Сміт К., 1980, с. 234.
- Спаркс, 1979, с. 66.
- Ендертон, 1977, с. 92.
- Ширлет, 2013, с. 43.
- Ендертон, 1977, с. 104.
Посилання
- Додавання // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.
