Інваріант графа
Інваріант графа в теорії графів — деяке значення (зазвичай числове) або упорядкований набір значень (хеш-функція), яке характеризує структуру графа і не залежить від способу позначення вершин або графічного зображення графа. Відіграє важливу роль при перевірці ізоморфізму графів, а також в задачах комп'ютерної хімії.
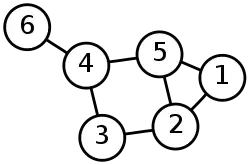
Приклади інваріантів
До інваріантів графа відносяться:
- Діаметр графа — довжина найкоротшого шляху (відстані) між парою найвіддаленіших вершин.
- Інваріант Колен де Вердьєра.
- Індекс Вінера[1][2] — величина
- ,
- де — мінімальна відстань між вершинами і .
- Індекс Рандича — величина
- .
- Індекс Хосойі — число парувань ребер графа плюс один.
- Міні-код і максі-код матриці суміжності, які одержують шляхом виписування двійкових значень матриці суміжності в рядок з подальшим переведенням отриманого двійкового числа в десяткову форму. Міні-коду відповідає такий порядок слідування рядків і стовпців, при якому отримане значення є мінімально можливим; максі-коду — відповідно максимальним.
- Мінімальне число вершин, яке необхідно вилучити для отримання незв'язного графа.
- Мінімальне число ребер, яке необхідно вилучити для отримання незв'язного графа.
- Мінімальне число вершин, необхідне для покриття ребер.
- Мінімальне число ребер, необхідне для покриття вершин.
- Нещільність графа — число вершин максимального по включенню безреберного підграфа (найбільша кількість попарно несуміжних вершин). Легко помітити, що та .
- Охоплення графа — число ребер в складі мінімального циклу.
- Визначник матриці суміжності.
- Щільність графа — число вершин максимальної по включенню кліки.
- Упорядкований за зростанням або спаданням вектор степенів вершин . В алгоритмах перебору для визначення ізоморфізму графів як можливо-ізоморфні пари вершин вибираються вершини з однаковими степенями, що сприяє зменшенню трудомісткості перебору. Використання даного інваріанта для k-однорідних графів не приводить до зниження обчислювальної складності перебору, так як степені всіх вершин таких графів однакові: .
- Упорядкований за зростанням або спаданням вектор власних чисел матриці суміжності графа (спектр графа). Сама по собі матриця суміжності не є інваріантом, так як при зміні нумерації вершин вона зазнає перестановки рядків і стовпців.
- Число вершин і число дуг/ребер .
- Число компонент зв'язності графа .
- Число Хардвігера .
- Характеристичний многочлен матриці суміжності.
- Хроматичне число .
Як інваріант можна розглядати не одне з наведених вище чисел, а їх кортеж (суперіндекс) виду , якому, у свою чергу, може бути зіставлений многочлен виду
сумування ведеться до останнього відмінного від нуля значення . Подібним чином можна ввести ще кілька інваріантів графа:
- , де — число вершин степеня i;
- , де — число безреберних підграфів з і вершинами;
- , де — число повних i-вершинних підграфів (i-клік);
- , де — число різних стягувань зв'язного графа на i-кліку;
- , де — число компонент зв'язності з і вершин;
- , де — число i-розфарбувань графа (правильних розфарбувань з використанням і кольорів).
Системи інваріантів графа, залежні від двох і більше параметрів, можна записати у вигляді многочленів від кількох формальних змінних Наприклад:
- , де — число підграфів графа , які мають вершин і ребер;
- , де — кількість i-вершинних підграфів, для яких число голок (ребер, які з'єднують вершини підграфа з іншими вершинами графа) дорівнює ;
- , де — кількість i-вершинних підграфів, які мають ребер і голок (узагальнення інваріантів і );
- Поліном Татта.
Збіг інваріантів є необхідною, але не достатньою умовою наявності ізоморфізму[3]
Повний інваріант
Інваріант називається повним, якщо збіг інваріантів графів є необхідним і достатнім для встановлення ізоморфізму. Наприклад, кожне зі значень і є повним інваріантом для графа з фіксованим числом вершин .
Трудомісткість обчислення
Інваріанти розрізняються за трудомісткістю обчислення. Інваріанти , , і обчислюються тривіально, в той час, як обчислення інваріантів , , , , , і залежних від них може бути досить обчислювально важким. Існують ймовірнісні алгоритми визначення значень наведених «важкообчислюваних» інваріантів, однак застосування подібних алгоритмів допускається не завжди.
В даний час повний інваріант графа, обчислюваний за поліноміальний час, невідомий, проте не доведено, що він не існує. Спроби його відшукання неодноразово робилися в 60-х — 80-х роках XX століття, однак не увінчалися успіхом.
Застосування в комп'ютерній хімії
Багато інваріантів (топологічні індекси) використовуються в комп'ютерній хімії для вирішення широкого кола загальних і спеціальних завдань[4]. До цих завдань відносяться: пошук речовин з наперед заданими властивостями (пошук залежностей типу «структура-властивість», «структура-фармакологічна активність»), первинна фільтрація структурної інформації для безповторної генерації молекулярних графів заданого типу та ряд інших. Часто при цьому поряд з топологічними індексами (залежними тільки від структури молекули) використовується інформація і про хімічний склад з'єднання[5].
Див. також
Примітки
- Wiener, H. (1947). Structural determination of paraffin boiling points. Journal of the American Chemical Society 1 (69): 17–20. doi:10.1021/ja01193a005..
- Rouvray, Dennis H. (2002). The rich legacy of half a century of the Wiener index. У Rouvray, Dennis H.; King, Robert Bruce. Topology in Chemistry: Discrete Mathematics of Molecules. Horwood Publishing. с. 16–37..
- Зыков А. А. Основы теории графов. — М. : Наука, 1986. — 384 с. — ISBN 978-5-9502-0057-1.
- Химические приложения топологии и теории графов = Chemical Applications of Topology and Graph Theory / Под ред. Р. Кинга. — М. : Мир, 1987. — 560 с.
- М. И. Трофимов, Е. А. Смоленский, Известия Академии наук. Серия химическая, 2005, 2166—2176.