Гаусівський пучок

Гаусівський пучок (син. Гаусів пучок) — пучок електромагнітного випромінювання, в якому розподіл електричного поля і випромінювання в поперечному перерізі добре апроксимується функцією Гауса. Когерентний світловий пучок з гаусовим розподіленням поля має фундаментальне значення в теорії хвильових пучків. Цей пучок називають основною модою на відміну від інших мод більш високого порядку.

Математичний опис

Шукається розв'язок наведеного хвильового рівняння, що описує поширення такого пучка у вигляді[1]:

\Psi =u(x,y,z)e^{ikz}

,

де $u(x,y,z)$ — повільно змінювальна комплексна функція, яка і визначає властивості лазерного пучка, що відрізняють його від плоскої хвилі. Застосування оператора Δ до функції Ψ дає:

\Delta \Psi =\left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}+2ik{\frac {\partial u}{\partial z}}-k^{2}u\right)e^{ikz}

.

Якщо у виразі знехтувати другою похідною $u$ по $z$ в порівнянні з першою, то на підставі наведеного хвильового рівняння Гельмгольца виходить рівняння:

{\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+2ik{\frac {\partial u}{\partial z}}=0

.

Отримане рівняння відноситься до рівнянь параболічного типу, а саме наближення, в рамках якого воно було отримано, називається параболічним наближенням. Неважко показати, що рівняння буде задовольняти гаусів пучок, амплітуда якого змінюється по поперечній координаті гаусового закону.

Для гаусового пучка можна записати вираз:

u=a\exp {\left[i\left(p+{\frac {k}{2q}}r^{2}\right)\right]}

,

де r²=x²+y². Параметр р — комплексний фазовий зсув при розповсюджені світла уздовж осі z, а q — комплексний параметр пучка, що визначає гаусовий розподіл поля по координаті r, де r — відстань від осі. Крім того, q визначає кривизну хвильового фронту, який поблизу осі є сферичним.

Розглянемо властивості гаусового пучка з довжиною хвилі λ більш докладно. Для цього висловимо комплексний параметр q через два дійсних параметра пучка R і w

{\frac {1}{q}}={\frac {1}{R}}+i{\frac {\lambda }{\pi w^{2}}},

де R — це радіус кривизни хвильового фронту, а w характеризує зміну поля Е в поперечній площині (параметр w прийнято називати шириною пучка). Розподіл поля в цій площині, підкоряється закону Гауса, і w дорівнює відстані, на якому амплітуда поля зменшується в е разів у порівнянні з полем на осі.

Властивості пучка

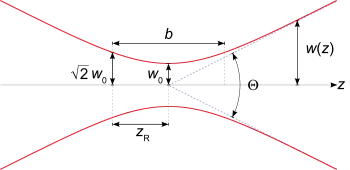
Ширина гаусового пучка w(z) як функція z. w₀: горловина пучка; b: глибина різкості; z_R: довжина Релея; Θ: кутова розбіжність пучка

Ширина пучка

В деякій площині, так званою горловиною каустичної поверхні або перетяжкою, гаусів пучок стягується до мінімальної ширини w₀. У цій площині, від якої доцільно відраховувати відстань z, фазовий фронт є плоским, і комплексний параметр пучка стає чисто уявним:

q_{0}={\frac {\pi w_{0}^{2}}{i\lambda }},z_{R}=iq_{0},

де z_R — довжина Релея. Тоді ширина пучка на відстані z задається наступною формулою:

w(z)=w_{0}{\sqrt {1+\left({\frac {\lambda z}{\pi w_{0}^{2}}}\right)^{2}}}

Радіус кривизни

Залежність радіуса кривизни від координати:

R(z)=z\left(1+\left({\frac {\pi w_{0}^{2}}{\lambda z}}\right)^{2}\right)

Розбіжність пучка

Твірна пучка w(z) представляє собою гіперболу, асимптота якої нахилена до осі під кутом

\theta ={\frac {\lambda }{\pi w_{0}}}

.

Цей кут дорівнює куту дифракції основної моди в дальній зоні.

Загальна кутова розбіжність пучка складе

\Theta =2\theta

.

Моди вищих порядків

Перші дев'ять емритово-гаусових мод

Гаусові пучки — всього одне з можливих розв'язків параксіального хвильового рівняння. Комбінації різних ортогональних розв'язків використовується для моделювання лазерних пучків. В загальному випадку, якщо визначений повний базис розв'язків, то будь-який пучок може бути описаним як суперпозиція розв'язків з базиса.

Джерела

Короленко, П. В. Оптика когерентного излучения. www.google.com (Російська). Процитовано 21 вересня 2021.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[math-1] Короленко, П. В. Оптика когерентного излучения. www.google.com (Російська). Процитовано 21 вересня 2021.