Горизонтальна система координат
Горизонта́льна систе́ма координа́т[1], або горизонтна система координат[2] — це система небесних координат, в якій основною площиною є площина математичного горизонту, а полюсами — зеніт і надир. Вона застосовується під час спостереження зірок і руху небесних тіл Сонячної системи на місцевості неозброєним оком, в бінокль або телескоп з азимутальною установкою[1]. Горизонтальні координати не тільки планет і сонця, але й зірок безперервно змінюються протягом доби через добове обертання небесної сфери.
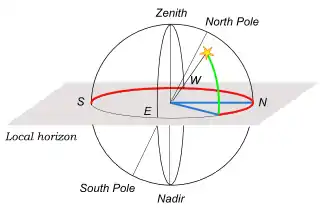
Опис
Лінії й площини
Горизонтальна система координат завжди топоцентрична. Спостерігач знаходиться у фіксованій точці на поверхні землі (позначена буквою О на малюнку). Припустимо, що спостерігач знаходиться в Східній півкулі Землі на широті φ. За допомогою виска визначається напрям на зеніт (Z) — верхню точку, в яку направлений висок, а надир (Z') — нижня точка (під Землею)[3]. Тому лінія (ZZ'), що з'єднує зеніт і надир називається висковою лінією[4].
Площина, перпендикулярна висковій лінії в точці О називається площиною математичного горизонту. На цій площині визначається напрям на Південь (географічний, не магнітний!) і Північ, наприклад, в найкоротшому напрямку за день тіні від гномону. Найкоротшою вона буде в істинний полудень, і лінія (NS), що з'єднує південь з північчю називається південною лінією[5]. Точки сходу (E) і заходу (W) віддаляються на 90 градусів від точки півдня відповідно проти й по ходу годинникової стрілки, якщо дивитися із зеніту. Таким чином, NESW — площина математичного горизонту.
Площина, що проходить через полуденну і вискову лінії (ZNZ'S) називається площиною небесного меридіана, а площина, що проходить через небесне тіло — площиною вертикального кола даного небесного тіла. Велике коло, по якому вона перетинає небесну сферу, називається вертикального кола небесного тіла[6].
Координати
У цій системі основною площиною є площина математичного горизонту. Однією координатою при цьому є або висота світила над горизонтом h, або його зенітна відстань z. Іншою координатою є азимут A.
- Висотою h світила називається дуга вертикального кола від математичного горизонту до світила, або кут між площиною математичного горизонту і напрямком на світило.
Висоти відраховуються в межах від 0° до +90° до зеніту і від 0° до −90° до надиру[6].
- Зенітною відстанню z світила називається дуга вертикального кола від зеніту до світила, або кут між прямовисною лінією і напрямком на світило.
Зенітні відстані відраховуються в межах від 0° до 180° від зеніту до надиру.
- Азимутом A світила називається дуга математичного горизонту від точки півдня до вертикального кола світила, або кут між полудневою лінією та лінією перетину площини математичного горизонту з площиною вертикального кола світила.
Азимути відраховують у бік добового обертання небесної сфери, тобто на захід від точки півдня, в межах від 0° до 360°. Іноді азимути відраховують від 0° до +180° на захід та від 0° до −180° на схід[7]. (У геодезії та навігації азимути відраховують від точки півночі[8].)
Особливості зміни координат небесних тіл
За добу зірка (а також в першому наближенні — тіло Сонячної системи) описує коло, перпендикулярне осі світу (PP'), яка на широті φ нахилене до математичного горизонту на кут φ. Тому вона буде рухатися паралельно математичному горизонту лише при φ рівному 90 градусів, тобто на Північному полюсі. Тому всі зірки, видимі там, не будуть заходити (у тому числі й Сонце протягом півроку, див. довгота дня) а їхня висота h буде постійною. На інших широтах доступні для спостережень в цей час року зірки діляться на
- ті, що заходять, і висхідні[9] (h протягом доби проходить через 0);
- ті, що не заходять[9] (h завжди понад 0);
- невисхідні[9] (h завжди менш як 0).
Максимальна висота h зірки буде спостерігатися раз у день при одному з двох її проходжень через небесний меридіан — верхній кульмінації, а мінімальна — при нижній кульмінації. Від нижньої до верхньої кульмінації висота h зірки збільшується, від верхньої до нижньої — зменшується.
Перехід до першої екваторіальної
Додатково до площини горизонту NESW, вискової лінії ZZ' і осі світу PP' накреслимо небесний екватор, перпендикулярний до PP' в точці O. Позначимо t — часовий кут світила, δ — його схилення, R — саме світило, z — його зенітна відстань. Тоді горизонтальну і першу екваторіальну систему координат зв'яже сферичний трикутник PZR, який називається першим астрономічним трикутником[10], або параллактичним трикутником[11]. Формули переходу від горизонтальної системи координат до першої екваторіальної системи координат мають наступний вигляд[12]:
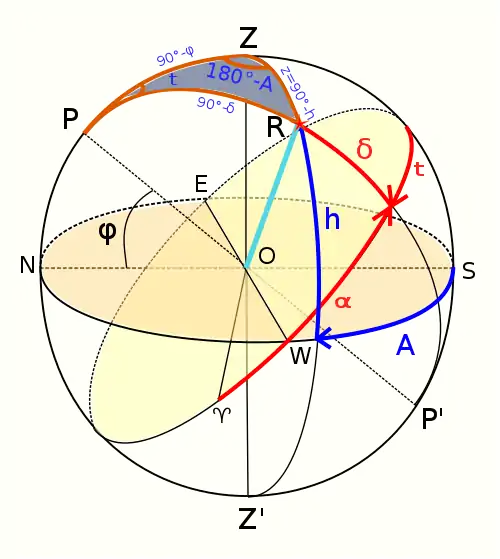
Послідовність застосування формул сферичної тригонометрії до сферичного трикутника PZR така ж, як при виведенні подібних формул для екліптичної системи координат: теорема косинусів, теорема синусів і формула п'яти елементів[13]. За теоремою косинусів маємо:
Перша формула отримана. Тепер до того ж сферичного трикутника застосовуємо теорему синусів:
Друга формула отримана. Тепер застосовуємо до нашого сферичноuj трикутнику формулу п'яти елементів:
Третя формула отримана. Отже, всі три формули отримані з розгляду одного сферичного трикутника.
Перехід від першої екваторіальної
Формули переходу від першої екваторіальної системи координат до горизонтальної системи координат виводяться при розгляді того ж сферичного трикутника, застосовуючи до нього ті ж формули сферичної тригонометрії, що і при зворотному переході[14]. Вони мають такий вигляд[15]:
Примітки
- Цесевич В. П. Що і як спостерігати на небі. — 6-е вид. — М.: Наука, 1984. — С. 85 — 304 с.
- Бєлова Н. А. Курс сферичної астрономії. — М.: Недра, 1971. — С. 30 — 183 с.
- Цесевич В. П. Що і як спостерігати на небі. — 6-е вид. — М.: Наука, 1984. — С. 38 — 304 с.
- Воронцов-Вельямінов Б. А. Астрономія: Підруч. для 10 кл. серед. шк. — 17-е изд. — М.: Просвещение, 1987. — С.12 — 159 с.
- Цесевич В. П. Що і як спостерігати на небі. — 6-е вид. — М.: Наука, 1984. — С. 39 — 304 с.
- Цесевич В. П. Що і як спостерігати на небі. — 6-е вид. — М.: Наука, 1984. — С. 40 — 304 с.
- Цесевич В. П. Що і як спостерігати на небі. — 6-е вид. — М.: Наука, 1984. — С. 41 — 304 с.
- Н.Олександрович «Горизонтальна система координат» Архівовано березень 20, 2012 на сайті Wayback Machine.
- Воронцов-Вельямінов Б. А. Астрономія: Підруч. для 10 кл. серед. шк. — 17-е изд. — М.: Просвещение, 1987. — С.16 — 159 с.
- Цесевич В. П. Що і як спостерігати на небі. — 6-е вид. — М.: Наука, 1984. — С. 68 — 304 с.
- Бєлова Н. А. Курс сферичної астрономії. — М.: Недра, 1971. — С. 36 — 183 с.
- Балк М. Б., Дьомін В. Г., Куніцин А. Л. Збірник завдань з небесної механіки та космодінаміки. — М.: Наука, 1972. — С. 18 — 336 с.
- Бєлова Н. А. Курс сферичної астрономії. — М.: Недра, 1971. — С. 37 — 183 с.
- Бєлова Н. А. Курс сферичної астрономії. — М.: Недра, 1971. — С. 37 — 183 с.
- Балк М. Б., Дьомін В. Г., Куніцин А. Л. Збірник завдань з небесної механіки та космодінаміки. — М.: Наука, 1972. — С. 17 — 336 с. (рос.)
