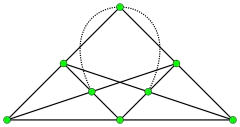
Граф Мебіуса — Кантора
У теорії графів гра́фом Ме́біуса — Ка́нтора називається симетричний двочастковий кубічний граф з 16 вершинами і 24 ребрами, названий на честь Августа Фердинанда Мебіуса і Зелігмана Кантора (1857—1903). Його можна визначити як узагальнений граф Петерсена G(8,3). Тобто, він утворений вершинами восьмикутника, з'єднаними з восьмикутною зіркою, в якій кожна точка з'єднана з третьої за рахунком точкою.
| Граф Мебіуса — Кантора | |
|---|---|
 | |
| Названий на честь | Август Фердинанд Мебіус і Зелігман Кантор |
| Вершин | 16 |
| Ребер | 24 |
| Радіус | 4 |
| Діаметр | 4 |
| Обхват | 6 |
| Автоморфізм | 96 |
| Хроматичне число | 2 |
| Хроматичний індекс | 3 |
| Genus | 1 |
| Властивості |
Симетричний Гамільтонів Двочастковий Кубічний Граф одиничних відстаней Граф Келі Досконалий |
Конфігурація Мебіуса — Кантора
Мебіус (Möbius 1828) поставив запитання, чи існує пара багатокутників з p сторонами в кожному, які володіють властивістю, що вершини одного багатокутника лежать на прямих, що проходять через сторони іншого, і навпаки. Якщо так, вершини і сторони цих багатокутників повинні утворювати проєктивну конфігурацію. Для p = 4 не існує рішення на евклідовій площині, але Кантор знайшов пару багатокутників такого типу в узагальненні завдання, в якому точки і ребра належать Комплексній проектованій площині. Тобто, у рішенні Кантора координатами вершин багатокутника є комплексні числа. Рішення Кантора для p = 4 — пара взаємно вписаних чотирикутника на комплексній проективної площини, називається конфігура́цією Ме́біуса — Ка́нтора. Граф Мебіуса — Кантора отримав своє ім'я від конфігурації Мебіуса — Кантора, оскільки він є графом Леві цій конфігурації. Граф має одну вершину для кожної точки конфігурації і по точці для кожної трійки, а ребра з'єднують дві вершини, якщо одна вершина відповідає точці, а інша трійці, що містить цю точку.
Зв'язок з гіперкубом
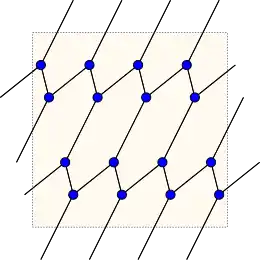
Граф Мебіуса — Кантора є підграфом чотиривимірного графу гіперкуба і утворений шляхом видалення восьми ребер з гіперкуба[1]. Оскільки гіперкуб є графом одиничних відстаней, граф Мебіуса — Кантора можна теж намалювати на площині з усіма сторонами одиничної довжини, хоча таке подання призведе до появи перехресних ребер.
Топологія
Граф Мебіуса — Кантора не можна вкласти в площину без перетинів, його число схрещувань дорівнює 4, і він є найменшим кубічним графом з таким числом схрещувань (послідовність A110507 в OEIS). Крім того, граф дає приклад графу, усі підграфи якого мають кількість перетинів на два і більше від кількості перетинів самого графу[2]. Однак він є тороїдальним — існує його вкладення в тор, при якому всі його грані є шестикутниками. Двоїстий граф цього вкладення — це граф гіпероктаедра K2,2,2,2.
Існує навіть більш симетричне вкладення графу Мебіуса — Кантора в подвійний тор, що є регулярним відображенням і має шестеро восьмикутних граней, в якому всі 96 симетрій графу можна здійснити як симетрії вкладення. Коксетер[3] приписує це вкладення Трелфалу.[4] 96-елемантну групу симетрії вкладення має граф Келі, який може бути вкладений в подвійній тор. Такер[5] показав, що це єдина група роду два. Скульптура Де Вітта Годфрея (DeWitt Godfrey) і Дуейн Мартинця (Duane Martinez) у вигляді подвійного тора з вкладеним графом Мебіуса — Кантора була представлена в Технічному музеї Словенії на шостій Словенської Міжнародній конференції з теорії графів в 2007. У 2013 обертаюча версія скульптури була представлена в Колгейтском університеті.
Граф Мебіуса — Кантора допускає вкладення в потрійний тор (тор третього роду), яке дає правильну карту, що має чотири 12-кутні грані[6].
Лижнен і Кулеманс,[7] досліджуючи можливі хімічні вуглецеві структури, вивчили родину усіх вкладень графу Мебіуса — Кантора в двовимірні многовиди. Вони показали, що існує 759 нееквівалентних вкладень.
Алгебраїчні властивості
- Група автоморфізмів графу Мебіуса — Кантора — це група порядку 96[8]. Вона діє транзитивно на вершини та на ребра, тому Граф Мебіуса — Кантора є симетричним.
- У нього є автоморфізми, які переводять будь-яку вершину в будь-яку іншу і будь-яке ребро в будь-яке інше.
- Згідно зі списком Фостера граф Мебіуса — Кантора є єдиним симетричним графом з 16 вершинами і найменшим кубічним симетричним графом, який не є дистанційно-транзитивним[9].
- Граф Мебіуса — Кантора є графом Келі.
Узагальнений граф Петерсена G (n, k) є вершинно-транзитивним в тому і тільки в тому випадку, коли n = 10 і k = 2 або коли k² ≡ ± 1 (mod n), і реберно-транзитивним тільки в наступних семи випадках: (n, k) = (4,1), (5,2), (8,3), (10,2), (10,3), (12,5), або (24,5) (Frucht, Graver, Watkins, 1971). Таким чином, граф Мебіуса — Кантора є одним з цих семи. Його симетричне вкладення в подвійній тор — одна з семи правильних кубічних карт, для яких загальне число вершин вдвічі більше числа вершин граней[10]. Серед семи симетричних узагальнених графів Петерсена знаходиться кубічний граф G (4,1), граф Петерсена G (5,2), граф додекаедра G (10,2), граф Дезарга G (10,3) і граф Науру G (12,5).
Характерний многочлен графу Мебіуса — Кантора дорівнює
Примітки
- Coxeter, 1950
- Dan McQuillan, R. Bruce Richter On the crossing numbers of certain generalized Petersen graphs // Discrete Mathematics. — 1992. — Т. 104, вып. 3. — С. 311—320.
- Coxeter, 1950.
- Threlfall, 1932.
- Tucker, 1984.
- Marušič, Pisanski, 2000
- Lijnen та Ceulemans, 2004.
- Royle, G. F016A data
- Conder, M.[en], Dobcsányi, P. «Trivalent Symmetric Graphs Up to 768 Vertices.» J. Combin. Math. Combin. Comput. 40, 41-63, 2002.
- McMullen, 1992
Джерела
- Coxeter, H. S. M. (1950). Self-dual configurations and regular graphs. Bulletin of the American Mathematical Society 56 (5): 413–455. doi:10.1090/S0002-9904-1950-09407-5. (англ.)
- Lijnen, E.; Ceulemans, A. (2004). Oriented 2-Cell Embeddings of a Graph and Their Symmetry Classification: Generating Algorithms and Case Study of the Möbius-Kantor Graph. J. Chem. Inf. Comput. Sci. 44 (5): 1552–1564. PMID 15446812. doi:10.1021/ci049865c. (англ.)
- Tucker, Thomas W. (1984). There is only one group of genus two. Journal of Combinatorial Theory, Series B 36 (3): 269–275. doi:10.1016/0095-8956(84)90032-7. (англ.)
- Threlfall, W. (1932). Gruppenbilder. Abhandlungen der Mathematisch-Physischen Klasse der Sächsischen Akademie der Wissenschaften 41 (6): 1–59. (нім.)
Посилання
- Weisstein, Eric W. Möbius-Kantor Graph(англ.) на сайті Wolfram MathWorld.
- Weisstein, Eric W. Möbius-Kantor Configuration(англ.) на сайті Wolfram MathWorld.