Граф Гофмана — Синглтона
У математичній теорії графів, граф Гофмана — Синглтона 7це -регулярнимйнеорієнтованимйграфозі 50 вершинами і 175 ребрами. Це єдиний сильно регулярний граф із параметрами (50,7,0,1)[4]. Його побудували Алан Гофман і Роберт Синглтон, коли намагалися класифікувати всі графи Мура, він є графом Мура з найвищим порядком, для якого відомо, що граф існує[5]. Оскільки це граф Мура, в якому кожна вершина має степінь 7, а обхват 5, тоді він є (7,5)-кліткою.
| Граф Гофмана — Синглтона | |
|---|---|
 | |
| Названий на честь |
Алан Гофман Роберт Синглтон |
| Вершин | 50 |
| Ребер | 175 |
| Радіус | 2 |
| Діаметр | 2[1] |
| Обхват | 5[1] |
| Автоморфізм |
252 000 (PSU(3,52):2)[2] |
| Хроматичне число | 4 |
| Хроматичний індекс | 7[3] |
| Властивості |
Сильно регулярний Симетричний Гамільтонів Цілий Клітка Граф Мура |
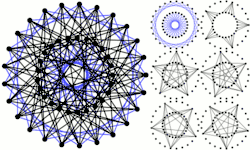
Побудова
Тут наведено дві побудови графа Гофмана — Синглтона.[6]
Побудова з п'ятикутників та пентаграм
Візьміть п'ять п'ятикутників Ph і п'ять пентаграми Qi, так щоб вершина j з Ph була суміжною з вершинами j−1 та j+1 з Ph і вершина j з Qi була суміжною з вершинами j−2 та j+2 з Qi. Тепер приєднайте вершину j з Ph до вершини h·i+j з Qi. (Всі індекси за модулем 5.)[6]
Побудова з площин Фано
Будь-яку множину зі семи точок (як абстрактних математичних об'єктів) можна перетворити на площину Фано, додавши сім ліній на них. Кількість різних способів зробити це — 30 = 7!/168. Тут 7! — це число перестановок із семи точок. 168 — число симетрій площини Фано, і, як наслідок, кількість перестановок, які зберігають будь-який заданий набір ліній, які утворюють площину Фано. Серед цих 30 різних площин Фано, кожна підмножина трьох точок використовується як лінія в 6 з 30 площин. Для будь-якої з цих 30 площин Фано, є 14 інших, які розділяють принаймні один рядок з ними.
Також сама множина з семи точок теж має 35 різних підмножин, які складаються з трьох елементів («тріад»), підрахованих за допомогою біноміального коефіцієнта .
Граф Гофмана — Синглтона в такому разі можна побудувати з двох множин вершин:
- по одній для кожної площини Фано в наборі з 15 площин, які формуються вибором однієї довільної і 14 інших, які розділяють лінію з ним, та
- по одній для кожної тріади.
Ці вершини з'єднані ребрами двох типів:
- між кожною вибраною площиною Фано і 7 тріад, які відповідають її лінії, та
- між тріадами зі спільних точок.[6]
Алгебраїчні властивості
Група автоморфізмів графа Гофмана — Синглтона є групою порядку 252 000 ізоморфною PΣU(3,52) напівпрямому добутку проєктивної спеціальної унітарної групи PSU(3,52) з циклічною групою порядку 2, породженої автоморфізму Фробеніуса. Він діє транзитивно на вершини, ребра і дуги графа. Тому граф Гофмана — Синглтона симетричний граф. Стабілізатор вершини графа є ізоморфом симетричної групи S7 по 7 букв. Стабілізатор множини ребер ізоморфний Aut(A6)=A6.22, де A6 є знакозмінною групою по 6 букв. Обидва з цих двох типів стабілізаторів є максимальними підгрупами всієї групи автоморфізмів графа Гофмана — Синглтона.
Характеристичний поліном графа Гофмана — Синглтона дорівнює . Тому граф Гофмана — Синглтона є інтегральним графом: його спектр повністю складається з цілих чисел.
Підграфи
Використовуючи тільки той факт, що граф Гофмана — Синглтона є сильно регулярним графом із параметрами (50,7,0,1), можна показати, що існує 1260 5-циклів, що містяться у графі Гофмана — Синглтона.
Крім того, граф Гофмана — Синглтона містить 525 копій графа Петерсена. Видалення будь-якого одного з них залишає копію унікальної (6,5)-клітки.[7]
Див. також
- Таблиця найбільших відомих графів заданого діаметра і максимального степеня
Примітки
- Weisstein, Eric W. Hoffman-Singleton Graph(англ.) на сайті Wolfram MathWorld.
- Hafner, P. R. "The Hoffman-Singleton Graph and Its Automorphisms." J. Algebraic Combin. 18, 7-12, 2003.
- Royle, G. "Re: What is the Edge Chromatic Number of Hoffman-Singleton?" GRAPHNET@istserv.nodak.edu posting. Sept. 28, 2004.
- Brouwer, Andries E.. Hoffman-Singleton graph..
- Hoffman, Alan J.; Singleton, Robert R. (1960). Moore graphs with diameter 2 and 3. IBM Journal of Research and Development 5 (4): 497–504. MR 0140437. doi:10.1147/rd.45.0497..
- Baez, John (1 лютого 2016). Hoffman–Singleton Graph. Visual Insight (American Mathematical Society).
- Wong, Pak-Ken. On the uniqueness of the smallest graph of girth 5 and valency 6. Journal of Graph Theory 3: 407–409. doi:10.1002/jgt.3190030413.
Посилання
- Benson, C. T.; Losey, N. E. (1971). On a graph of Hoffman and Singleton. Journal of Combinatorial Theory. Series B 11 (1): 67–79. ISSN 0095-8956. MR 0281658. doi:10.1016/0095-8956(71)90015-3.
- Holton, D.A.; Sheehan, J. (1993). The Petersen graph. Cambridge University Press. с. 186 and 190. ISBN 0-521-43594-3..