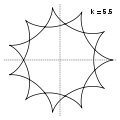
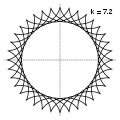
Гіпоциклоїда
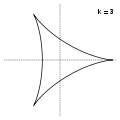
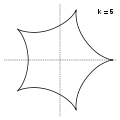
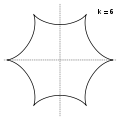
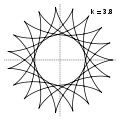
Гіпоцикло́їда (від грецьких слів ὑπό — під, внизу і κύκλος — круг, коло) — плоска крива, що утворюється точкою кола, що котиться по внутрішній стороні іншого кола без проковзування.
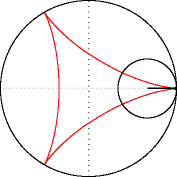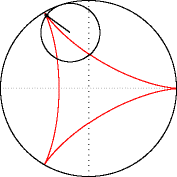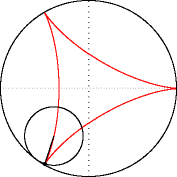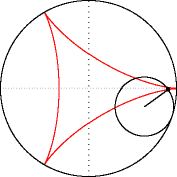
Рівняння
де , де — радіус нерухомого кола, — радіус кола, що котиться.
Нехай у початковий момент кола дотикаються в точці А, що лежить на осі OX, де т.О - центр великого кола. Координати т.А при цьому - (kr, 0), де R / r = k. Розглянемо, як змінюються координати т.А, прив'язаної до кола, що котиться (т.А переходить у т.A'). Нехай маленьке коло прокотилося так, що його центр перейшов з т.C в т.C' і повернувся щодо т.O на кут t. По-перше, можна показати, що поворот маленького кола щодо свого центру при цьому (тобто кут між CA і C'A') дорівнює t - kt = - (k-1) t. По-друге, координати т.C' будуть такими: ((k-1) r cos (t), (k-1) r sin (t)). Тоді, знаючи, куди перейде центр кола, що котиться, і на який кут воно повернулося щодо цього центру, можна записати координати т.А':
- X = (k-1) r cos (t) + r cos ((k-1) t)
- Y = (k-1) t sin (t) - r sin ((k-1) t)
Модуль величини визначає форму гіпоциклоїди. При гіпоциклоїда є діаметром нерухомого кола, при є Астроїдою.
Посилання
- J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. с. 168,171–173. ISBN 0-486-60288-5.
- Гіпоциклоїда на Javascript
- Weisstein, Eric W. "Hypocycloid." З сайту MathWorld--A Wolfram Web Resource[недоступне посилання з липня 2019]