Гіппократові серпки

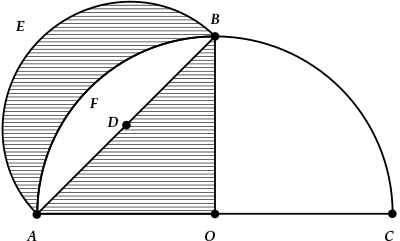
Гіппокра́тові серпки́[1][2][3] — утворені двома дугами з різним радіусом фігури, які описав Гіппократ Хіоський[4] в V столітті до н. е. Їх особливість в тому, що ці фігури можливо квадратурувати, тобто за допомогою циркуля і лінійки можна побудувати рівновеликі їм прямокутники. Гіппократ сподівався на цьому шляху вирішити проблему квадратури круга.

Гіппократовим серпком є ліва верхня заштрихована область. Її площа дорівнює площі заштрихованого трикутника в правій частині знизу.

Гіппократ отримав три квадратуровані серпки. Даніель Бернуллі в «Математичних вправах» (1724) вказав умову, яку повинні задовольняти алгебраїчно квадратуровні серпки, і привів рівняння, що дає четверту. Трохи пізніше, фінський математик М. Й. Валленіус (1766) і незалежно від нього Л. Ейлер (1771) також виявили ту ж четверту і на додаток до неї, ще п'яту. У 1840 році Томас Клаузен незалежно виявив і досліджував ті ж два негіппократових типи квадратуровних серпків. Пізніше, в 1930-і роки, М. Г. Чеботарьов і А. В. Дороднов довели, що інших типів квадратуровних серпків, крім зазначених п'яти, не існує.[5]

П'яти типам квадратуровних серпків відповідають такі відношення зовнішньої і внутрішньої дуг серпків.

Відкриті Гіппократом. 2:1; 3:2; 3:1. Кути: (180°:90°), (160,9°:107,2°), (205,6°:68,5°).

Дві наступні. 5:1; 5:3. Кути: (234.4°:46.9°) і (168.0°:100.8°).

Примітки
  1. Гіппократові серпки // Шляхами математики: Хрестоматія для учнів 5-9 кл. / Упоряд. Т.М. Хмара. - К., 1999.
  2. Гіппократові серпки // Математич. хрестоматія. – Київ : Радянська школа, 1968.
  3. Гіппократів // Великий тлумачний словник сучасної української мови — Видавництво «Перун», 2005.
  4. 1947-, Dunham, William, (1991, ©1990). Journey through genius : the great theorems of mathematics. New York: Penguin Books. ISBN 014014739X. OCLC 24168395.
  5. Shenitzer, A., Steprans, J. (1994). The Evolution of Integration (Англійська). Amer. Math. Monthly 101.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.