Дисперсія хвилі

Причиною виникнення залежності фазової швидкості від частоти можуть бути фізичні властивості середовища, в якому поширюється хвиля, або особливості геометрії області існування хвильового збурення. В залежності від цього розрізняють фізичну та геометричну дисперсію.

Основою для виділення особливих випадків дисперсії може бути характер залежності фазової швидкості від частоти. Якщо з ростом частоти фазова швидкість хвилі зростає говорять про аномальну дисперсію. Випадок, коли з ростом частоті фазова швидкість зменшується, визначають як нормальну дисперсію.

Хвилі на поверхні води формуються під дією двох відновлюючих сил: сили поверхневого натягу та сили гравітації[2]. У рамках моделі нестисливої рідини характеристики поверхневої хвилі визначаються гармонічною функцією потенціалу швидкостей, яка задовольняє рівняння Лапласа. Для двовимірного випадку гармонічної хвилі потенціал швидкостей має такий вигляд

${\displaystyle \phi (x,z,t)=\phi _{0}\sin(kx-\omega t)/\exp(-kz)}$.

Тут ${\displaystyle x}$ — координата вздовж поверхні рідини (напрямок поширення хвилі), ${\displaystyle z}$ — відстань від поверхні рідини, ${\displaystyle \omega }$ — кругова частота, ${\displaystyle t}$ — час. Із граничних умов на поверхні рідини у випадку хвиль, довжина яких ${\displaystyle \lambda =2\pi /k}$ значно більша амплітуди ${\displaystyle \phi _{0}k/\omega }$ встановлюється такий зв'язок між хвильовим числом ${\displaystyle k}$ та круговою частотою:

${\displaystyle \omega ={\sqrt {gk+{\frac {\sigma k^{3}}{\rho }}}}}$.

У цьому співвідношенні ${\displaystyle g}$ -прискорення вільного падіння, ${\displaystyle \sigma }$ — коефіцієнт поверхневого натягу, ${\displaystyle \rho }$ — густина рідини. Такі співвідношення між частотою та хвилевим числом в теорії хвиль називаються дисперсійними рівняннями. Дане рівняння встановлено для випадку нескінченної глибини води.

З приведеного дисперсійного рівняння випливає, що вплив поверхневого натягу на характер хвильового руху на поверхні води може бути суттєвим лише для хвиль з відносно малою довжиною (капілярні хвилі). Враховуючи значення коефіцієнту поверхневого натягу води ${\displaystyle \sigma =73\cdot 10^{-3}{\frac {H}{m}}}$ можна переконатись, що вплив поверхневого натягу може бути помітним лише для хвиль довжиною порядка частки міліметра. Для фазової швидкості хвиль на поверхні води без врахування поверхневого натягу маємо наступний вираз ${\displaystyle c_{f}={\frac {g}{\omega }}}$. Фазова швидкість зменшується з ростом частоти, що вказує на наявність нормальної дисперсії при поширенні хвиль на поверхні води. При такому типі дисперсії швидше поширюються хвилі з більшою довжиною. Якщо розглянути діапазон довжин хвиль від одного до ста метрів на поверхні глибокої води, то згідно з встановленим законом дисперсії їх фазова швидкість буде змінюватися від 1,25 м/c до 12,5 м/c. Ці значення фазової швидкості значно менші ніж швидкість звуку (1500 м/c) в воді, що дозволяє використовувати модель нестисливої рідини при вивченні властивостей гравітаційних хвиль. Для поверхневих хвиль з довжинами, для яких є суттєвим вплив сили поверхневого натягу, має місце аномальна дисперсія, коли фазова швидкість хвилі зростає зі зменшенням її довжини. Найменше значення фазової швидкості поверхневих хвиль на воді має місце для хвиль з довжиною 1,73 см. Це мінімальне значення становить 23,1 см/с.

У загальному випадку на характеристики хвиль на поверхні води впливає глибина водойми. Якщо вважати, що дно водойми глибиною ${\displaystyle H}$ є жорсткою недеформівною поверхнею (вертикальна складова вектора швидкості частинок води на цій поверхні дорівнює нулеві) дисперсійне співвідношення для поверхневих хвиль має вигляд ${\displaystyle \omega ={\sqrt {gk\operatorname {th} (kH)}}}$. При цьому нехтуємо ефектом поверхневого натягу. Для довгих хвиль в відносно мілкій водоймі маємо оцінку ${\displaystyle kH\ll 1}$. Тоді для гіперболічного тангенсу можна прийняти значення ${\displaystyle \operatorname {th} (kH)=kH}$ і вказане дисперсійне співвідношення трансформується до виду ${\displaystyle \omega =k{\sqrt {gH}}}$. У таких хвилях явище дисперсії не спостерігається і фазова швидкість практично визначається глибиною водойми.

Слід мати на увазі, що багато хвильових ефектів, що спостерігаються в природі не можна пояснити на основі приведених даних про дисперсійні властивості хвиль на воді. У поведінці таких хвиль часто важливу роль відіграють ефекти нелінійності. Дослідженню цих ефектів присвячено багато робіт, серед яких вкажемо[3][4].

При моделюванні процесів поширення та генерації хвиль в рідинах та газах широко використовується модель ідеальної стисливої рідини. В такому середовищі збурення можуть передаватися лише в вигляді хвиль розтягу-стиску (акустичні хвилі) зі швидкістю, яку називають швидкістю звуку[5]. У необмеженому об'ємі ідеальної стисливої рідини гармонічні хвилі поширюються без дисперсії. Явище дисперсії при поширенні акустичних хвиль спостерігається лише тоді, коли область існування звукового поля обмежена певними граничними поверхнями. Типовим прикладом такої ситуації є поширення акустичних хвиль в хвилеводах.

Частина модельного акустичного хвилеводу

На рисунку показано частину поверхні модельного хвилеводу, який використаємо для ілюстрації особливостей поширення акустичних хвиль. Такий модельний хвилевід утворено двома нескінченними жорсткими пластинками. Відстань між пластинками позначено як ${\displaystyle g}$. Розглянемо поширення гармонічного збурення, характеристики якого не змінюються по координаті ${\displaystyle y}$. Вважаємо, що збурення поширюється в напрямку координати ${\displaystyle z}$. Враховуючи, що потенціал звукового поля має задовольняти двовимірне хвильове рівняння та граничні умови на жорстких поверхнях ${\displaystyle x=0,x=g}$, Потенціал звукового поля у хвилеводі набуває вигляду[5]:${\displaystyle \phi _{n}(x,z,t)=a_{n}\cos {\frac {n\pi }{g}}x\cos(\gamma _{n}z-\omega t),n=1,2,3,\dots }$. Тут прийнято позначення: ${\displaystyle \gamma _{n}={\sqrt {k^{2}-\left({\frac {n\pi }{g}}\right)^{2}}},k={\frac {\omega }{c}}}$.

Аналіз проведених розв'язків хвильового рівняння показує що:

1. Хвилі, що поширюються у хвилеводі при заданій частоті можуть мати лише дискретні значення хвильового числа ${\displaystyle \gamma _{n}={\sqrt {k^{2}-\left({\frac {n\pi }{g}}\right)^{2}}}}$. Такі хвилі називають нормальними хвилями (модами) хвилеводу.
2. Таких хвиль при фіксованій частоті може бути лише скінченне число.
3. Фазова швидкість нормальних хвиль ${\displaystyle c_{f}={\frac {\omega }{\sqrt {k^{2}-\left({\frac {n\pi }{g}}\right)^{2}}}}}$ з ростом частоти змінюється від нескінченності (${\displaystyle k_{n}=n\pi /g}$) до величини швидкості звуку в вільному просторі ${\displaystyle k_{n}\gg n\pi /g}$. Значення частоти, що визначається рівністю ${\displaystyle k_{n}=n\pi /g}$ називається критичною частотою ${\displaystyle n}$-ї моди.

Такі властивості дисперсії є типовими практично для всіх типів хвилеводів[6].

В ізотропних пружних тілах існують два типи хвиль — поздовжні й поперечні[7]. Такі хвилі поширюються в середовищі без дисперсії з різними фазовими швидкостями, відповідно, швидкістю поздовжніх та поперечних хвиль.

Схематичне зображення двох типів хвиль Лемба в пружній пластині.

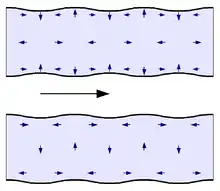
Перші дослідження дисперсійних властивостей хвиль у пружних тілах пов'язані з іменем англійського вченого Г. Лемба (Horace Lamb). У роботі, датованій 1917 роком, ним розглянуто двовимірну задачу про поширення хвиль в пружному шарі (пружній пластині) і одержано дисперсійні рівняння для двох типів хвиль — симетричної та антисиметричної відносно серединної площини шару. На рисунку зображено характер руху частинок пружного тіла при поширенні симетричної та антисиметричної хвилі Лемба. Стрілкою показано напрям поширення хвиль.

Залежності фазових швидкостей хвиль Лемба від частоти в пружній пластині

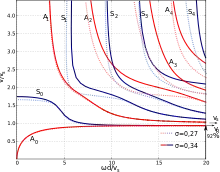
Хоча дисперсійні рівняння для пружних хвиль у двовимірному випадку одержані Лембом на початку 20 століття їх ґрунтовний аналіз проведено лише в роботах Р. Міндліна (Raymond D. Mindlin)[8]. Міндліном вказано ефективний метод аналізу дисперсійних рівнянь та пошуку всіх (дійсних, уявних та комплексних) коренів. Дійсні корені визначають дисперсійні властивості хвиль, що поширюються у хвилеводі. На рисунку представлено дані про фазові швидкості симетричних (сині криві)та антисиметричних (червоні криві) хвиль для двох матеріалів з різними значеннями коефіцієнта Пуасона. У випадку пружного хвилеводу в ньому можуть поширюватися хвилі, як з нормальною, так і з аномальною дисперсією.

Для фазових швидкостей симетричних та антисиметричних хвиль у пружній пластині встановлено певні граничні значення. Швидкості хвиль нижчих порядків ${\displaystyle A_{0},S_{0}}$ існують при будь-яких значеннях частоти й обмежені по величині в усьому частотному діапазоні. З ростом частоти їх величини прямують до значення фазової швидкості ${\displaystyle V_{R}}$ хвилі Релея (див. Поверхневі акустичні хвилі). Фазові швидкості всіх інших нормальних хвиль у пластині мають граничним значенням величину швидкості поперечних хвиль ${\displaystyle V_{S}}$ в матеріалі пружного тіла. Важливо, що ці нормальні хвилі можуть існувати лише в певних частотних діапазонах (як це видно на приведеному рисунку). Крім того, фазова швидкість таких хвиль може бути необмеженою. Ця обставина чітко вказує на те, що фазова швидкість хвилі не є характеристикою швидкості переносу енергії. Для аналізу цього процесу та визначення можливої швидкості передачі сигналу важливе значення має величина групової швидкості. Значення частоти, при якому фазова швидкість нормальної хвилі прямує до нескінченності називають критичною частотою для даної хвилі.

• Дисперсія світла