Фазова швидкість

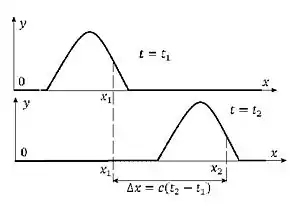
Фазова швидкість — одна із характеристик хвилі, що характеризує поширення збурення будь-якої фізичної природи. Поняття фазової швидкості може використовуватись при розповсюдженні збурень будь-якої форми, якщо в процесі розповсюдження ця форма не змінюється. На рисунку проілюстровано визначення фазової швидкості збурень в струні.[1]

До визначення фазової швидкості збурень в струні

Формули

Для загального випадку поширення хвиль у просторі важливе збереження форми збурення, а його амплітуда може зменшуватися за рахунок просторового розтікання енергії, як це відбувається в сферичній хвилі.

В багатьох випадках властивості середовища, в якому розповсюджується збурення, зумовлюють зміну форми збурення в процесі розповсюдження. Без зміни форми в таких випадках може розповсюджуватися лише гармонічна хвиля, в якій зміну величини збурення в часі можна подати у вигляді $W=a_{0}\cos(kx-\omega t)$ ,де $\omega$ — циклічна частота, k — хвильове число. Такі хвилі, які описують збурення з однією частотою часто називають монохроматичними. В цьому випадку фазова швидкість хвилі визначається як відношення її циклічної частоти до хвильового числа.

v_{ph}={\frac {\omega }{k}}

.

Це співвідношення можна переписати у вигляді:

v_{ph}={\frac {\lambda }{T}}

,

де $\lambda$ — довжина хвилі, T — її період.

Фазова швидкість завдячує своє назвою тому факту, що це швидкість переміщення в просторі точки з певною фазою. Для монохроматичної хвилі існує єдина, у загальному випадку залежна від частоти, фазова швидкість. Немонохроматичну хвилю можна розглядати як суперпозицію монохроматичних хвиль, кожна з яких має свою фазову швидкість. Якщо фазові швидкості різних монохроматичних складових хвилі різні, то хвильовий пакет розпливається, тобто з часом форма хвилі змінюється.

Ілюстрація фазової та групової швидкості. Червона точка рухається з фазовою швидкістю, а зелена з груповою

Залежність довжини хвилі від частоти задається законом дисперсії для відповідного виду хвиль і визначається природою хвиль та середовища, в якому вони розповсюджуються. У разі лінійного закону дисперсії фазова швидкість хвилі не залежить від частоти. Така ситуація реалізується, наприклад, для електромагнітних хвиль у вакуумі, де фазова швидкість дорівнює швидкості світла. Хвильовий пакет електромагнітних хвиль у вакуумі не розпливається. Лінійний закон дисперсії властивий також, наближено, звуковим хвилям чутного діапазону. Внаслідок цього звук не спотворюється з віддаллю.

Фазова швидкість електромагнітної хвилі

Фазова швидкість електромагнітної хвилі у середовищі визначається формулою

v_{ph}={\frac {c_{0}}{n(\omega )}}

,

де $c_{0}$ — швидкість світла у вакуумі, $n(\omega )$ — залежний від частоти показник заломлення. Показник заломлення більшості речовин в оптичному діапазоні перевищує одиницю, а тому фазова швидкість світла у речовині здебільшого менша від швидкості світла у вакуумі. Однак, поблизу смуг поглинання та при високих частотах показник заломлення може бути меншим від одиниці, і тоді фазова швидкість світла перевищує $c_{0}$ . Це не суперечить теорії відносності, оскільки фазова швидкість характеризує плоску монохроматичну хвилю, яка однакова у всьому просторі й безмежна в часі, а тому не може передавати інформацію. Інформація передається хвильовими пакетами, що розповсюджуються з груповою швидкістю, яка завжди менша від швидкості світла у вакуумі.

Для хвильового рівняння

Будь-яка хвиля, описувана хвильовим рівнянням

{\frac {\partial ^{2}f}{\partial t^{2}}}=C^{2}{\frac {\partial ^{2}f}{\partial x^{2}}}

,

має фазову швидкість $C$ (причому $C$ тут — деякий сталий коефіцієнт; цей коефіцієнт дорівнює швидкості світла в хвильовому рівнянні для електромагнітних хвиль).

Такий результат отримано прямою підстановкою в це рівняння монохроматичної хвилі вигляду $\cos(kx-\omega t)$ і потім обчисленням $\omega /k$ .

Цей результат правильний не тільки для хвильового рівняння на одновимірному просторі (ми його використовували вище лише для стислості; все залишається цілком аналогічним за будь-якої кількості похідних за координатами в правій частині).

Для рівняння Клейна — Ґордона

Рівняння Клейна — Ґордона

{\frac {\partial ^{2}f}{\partial t^{2}}}=C^{2}{\frac {\partial ^{2}f}{\partial x^{2}}}+C^{4}m^{2}f

,

яке відрізняється тільки останнім членом, дає за аналогічної підстановки

\omega ^{2}=C^{2}k^{2}+C^{4}m^{2}

,

звідки:

\omega ={\sqrt {C^{2}k^{2}+C^{4}m^{2}}}

і

v_{\varphi }=\omega /k=C{\sqrt {1+C^{2}m^{2}/k^{2}}}

.

Цей вираз за ненульових дійсних $m$ завжди більший, ніж $C$ , і може бути як завгодно великим при $k\rightarrow 0$ .

Фазова швидкість як вектор

У певному сенсі фазова швидкість не є вектором. Кажучи так, мають на увазі той факт, що фазові швидкості за різними напрямками (наприклад, за напрямками координатних осей), що визначаються так, як це описано вище, не є ні координатами, ні проєкціями[2] ніякого вектора[3]. Зокрема, очевидно, вони не є проєкціями або координатами вектора, що збігається за напрямком із хвильовим вектором, і з абсолютною величиною, рівною фазовій швидкості в цьому напрямку.

Але це, звичайно, не заважає, за бажання, ввести чисто формально вектор фазової швидкості, який, за визначенням, збігається за напрямком із хвильовим вектором і з абсолютною величиною, рівною фазовій швидкості в цьому напрямку. Питання про те, чи коректно називати такий вектор вектором фазової швидкості, є чисто термінологічним (конвенціональним). Фактом є лише те, що проєкції цього «вектора» на осі координат або компоненти за цими осями не будуть відповідати фазовій швидкості уздовж цих напрямків відповідно до визначення фазової швидкості за напрямком, даним на початку статті (і взагалі з якимсь розумним визначенням, крім чисто формального, описаного в цьому абзаці).

Конкретно ж, для випадку плоскої гармонічної хвилі фазову швидкість уздовж хвильового вектора можна виразити так:

v_{\phi }\equiv v_{\phi ,0}=\omega /k

,

де $k$ — хвильове число, $\omega$ — кутова частота. При цьому фазова швидкість уздовж напрямку, відхиленого від хвильового вектора на кут $\alpha$ , дорівнюватиме:

v_{\phi ,\alpha }={\frac {v_{k}}{\cos \alpha }}

Нерозуміння цього факту часто стає причиною непорозумінь і помилок. Наприклад, з наведеного вище ясно, що фазова швидкість може бути більшою від швидкості світла (це випливає прямо з написаної вище формули, враховуючи, що $\cos \alpha$ може набувати як завгодно малих значень при прямуванні кута до прямого, і, відповідно, фазова швидкість у напрямку, близькому до ортогонального, виявляється як завгодно великою, прямуючи до нескінченності)[4].

Чи може фазова швидкість перевищувати швидкість світла

Фазова швидкість може перевищувати швидкість світла у вакуумі, і нерідко її перевершує. Це ніяк не суперечить відомому принципу максимальності швидкості світла, необхідність якого виникає, щоб одночасно дотримувалися принцип причинності (щоб не виникало причинних парадоксів) і принцип відносності (лоренц-інваріантність).

Справа в тому, що ці принципи накладають обмеження тільки на швидкість поширення таких фізичних об'єктів, за допомогою яких можна передати інформацію. А фазова швидкість[5] не належить до швидкостей таких об'єктів. Чисто монохроматична (синусоїдальна) хвиля нескінченна в просторі і в часі, не може ніяк змінитися, щоб передати інформацію (якщо ми промодулюємо хвилю, вона перестане бути монохроматичною, а швидкість поширення модуляції не збігається з фазовою швидкістю, зазвичай збігаючись зі швидкістю груповою для майже монохроматичних хвиль).

Фазова швидкість у напрямку, що не збігається з хвильовим вектором

Оскільки фазова швидкість, виміряна вздовж довільного напрямку, що не збігається з хвильовим вектором і напрямком поширення хвилі, не є швидкістю руху «фізичного об'єкта», тобто об'єкта, стан якого в наступні моменти часу причинно обумовлений станом у попередні, а по суті характеризує просто стан осцилювального поля в штучно вибраних точках, часто (а саме якщо вибрати достатньо великий кут з хвильовим вектором) фазова швидкість у цьому напрямку будь-якої, навіть як завгодно повільної (як показано в абзаці вище) хвилі може перевищувати швидкість світла, прямуючи до нескінченності при наближенні кута до прямого.

Зокрема, фазова швидкість світла (або взагалі будь-якої біжучої електромагнітної хвилі) у вакуумі, виміряна в будь-якому напрямку, що не збігається з її хвильовим вектором, завжди більша від швидкості світла.

Але справа не обмежується фазовою швидкістю в довільному напрямку. Швидкість світла може бути перевищена навіть і фазовою швидкістю, виміряною вздовж хвильового вектора.

Фазова швидкість для квантової частинки

Фазова швидкість квантової «хвилі», що відповідає будь-якій масивній частинці (тобто частинці, що має масу більшу від нуля), завжди більша від швидкості світла. Це легко бачити з формул $\ v_{\phi }=\omega /k$ , $E=\hbar \omega$ і $p=\hbar k$ , з чого $\ v_{\phi }=E/p$ , тоді як $E$ для масивних частинок завжди більше від $p$ за рахунок маси (енергії спокою).

Однак ця фазова швидкість в принципі не може спостерігатися (оскільки у квантовій фізиці фаза не спостерігається взагалі). Доступна ж для спостереження лише групова швидкість, яка і є квантовим аналогом звичайної швидкості класичної частинки.

Фазова швидкість для рівняння Клейна — Ґордона

Але диференціальні рівняння, що описують квантові частинки, можна реалізувати й на інших фізичних системах (наприклад, на досить простих механічних моделях). У цьому випадку фазова швидкість цілком доступна для спостереження.

Проте й тут фазову швидкість можна зробити як завгодно великою (достатньо підібрати досить мале k), і, в принципі, її неважко зробити більшою, ніж швидкість світла.

Цей на вигляд парадоксальний результат пов'язаний з тим, що «поширення» такої хвилі є ілюзією[6] в тому сенсі, що між різними частинами хвилі немає причинного зв'язку (стан хвилі, що просунулася вправо, не визначається тим, якою вона була зліва).

Див. також

Примітки

В. Т. Грінченко, І. В. Вовк, В. Т. Маципура (2007). Основи акустики: Навчальний посібник. Київ: Наукова думка.
За використання, наприклад, косокутних координат поняття координати вектора та проєкції на вісь не збігаються.
Звичайно, в певній фіксованій системі координат будь-яка трійка (говоримо, для визначеності, про тривимірний випадок) чисел визначає вектор; однак, якщо ми маємо справу з цим вектором, то при зміні системи координат (наприклад, при повороті осей) ми повинні отримати узгоджені за певними правилами результати для будь-якої системи координат, а вже таке виявляється хибним для трійки чисел, яку ми розглядаємо.
Це не суперечить теорії відносності. Див. наступий параграф.
Як, наприклад, і швидкість зайчика на екрані — див. статтю Надсвітловий рух.
Поширення як факт, звісно, має місце; під ілюзією тут розуміється те, що ми схильні інтуїтивно вкладати в цей факт більше, ніж у ньому реально є, а саме ми інтуїтивно схильні вважати, що для хвилі, яка рухається ліворуч, попередні стани хвилі ліворуч є причиною наступних станів праворуч, що не так. Насправді правильніше було б сказати, що різні частини цієї хвилі коливаються незалежно одна від одної, і накладання таких коливань і дає біжучу хвилю (справді, нагадує оптичний обман).

Література

В. Т. Грінченко, І. В. Вовк, В. Т. Маципура (2007). Основи акустики: Навчальний посібник. Київ: Наукова думка.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[hrinchenko-1] В. Т. Грінченко, І. В. Вовк, В. Т. Маципура (2007). Основи акустики: Навчальний посібник. Київ: Наукова думка.

[2] За використання, наприклад, косокутних координат поняття координати вектора та проєкції на вісь не збігаються.

[3] Звичайно, в певній фіксованій системі координат будь-яка трійка (говоримо, для визначеності, про тривимірний випадок) чисел визначає вектор; однак, якщо ми маємо справу з цим вектором, то при зміні системи координат (наприклад, при повороті осей) ми повинні отримати узгоджені за певними правилами результати для будь-якої системи координат, а вже таке виявляється хибним для трійки чисел, яку ми розглядаємо.

[4] Це не суперечить теорії відносності. Див. наступий параграф.

[5] Як, наприклад, і швидкість зайчика на екрані — див. статтю Надсвітловий рух.

[6] Поширення як факт, звісно, має місце; під ілюзією тут розуміється те, що ми схильні інтуїтивно вкладати в цей факт більше, ніж у ньому реально є, а саме ми інтуїтивно схильні вважати, що для хвилі, яка рухається ліворуч, попередні стани хвилі ліворуч є причиною наступних станів праворуч, що не так. Насправді правильніше було б сказати, що різні частини цієї хвилі коливаються незалежно одна від одної, і накладання таких коливань і дає біжучу хвилю (справді, нагадує оптичний обман).