Гіперболічні функції
Гіперболі́чні фу́нкції — сімейство елементарних функцій, які виражаються через експоненту і тісно пов'язані з тригонометричними функціями.
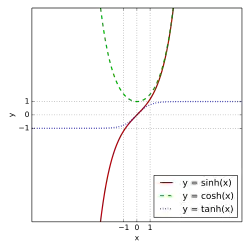
Визначення
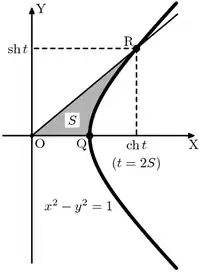
Гіперболічні функції задаються такими формулами:
- гіперболічний синус:
- (в іноземній літературі позначається ).
Існує сленгова назва: «шинус».
- гіперболічний косинус:
- (в іноземній літературі позначається ).
Існує сленгова назва: «чосинус», «кошинус».
Лінію гіперболічного косинуса називають ланцюговою, бо саме таку форму приймає ланцюг або мотузка, яку підвісили за обидва кінці в однорідному гравітаційному полі.
- гіперболічний тангенс:
- (в іноземній літературі позначається ).
Існують сленгові назви: «щангенс», «цангенс».
Іноді також визначається
- гіперболічний котангенс:
- ,
- гіперболічні секанс і косеканс:
- ,
- .
Властивості
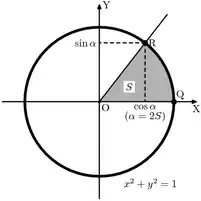
Зв'язок з тригонометричними функціями
Гіперболічні функції виражаються через тригонометричні функції від уявного аргументу.
.
.
Функція Гудермана зв'язує тригонометричні функції та гіперболічні функції без залучення комплексних чисел.
Важливі тотожності
- .
- Парність:
- ,
- ,
- .
- Формули додавання:
- ,
- ,
- .
- Формули подвоєного кута:
- ,
- ,
- ,
- ,
- ,
- .
- Формули кратних кутів:
- ,
- ,
- ,
- ,
- ,
- .
- Добуток
- ,
- ,
- ,
- .
- Суми
- ,
- ,
- ,
- .
- Формули пониження степеня
- ,
- .
- Похідні:
- ,
- ,
- ,
- ,
- ,
- .
- Інтеграли:
- ,
- ,
- ,
- ,
- .
Нерівності
При всіх виконується
- ,
- .
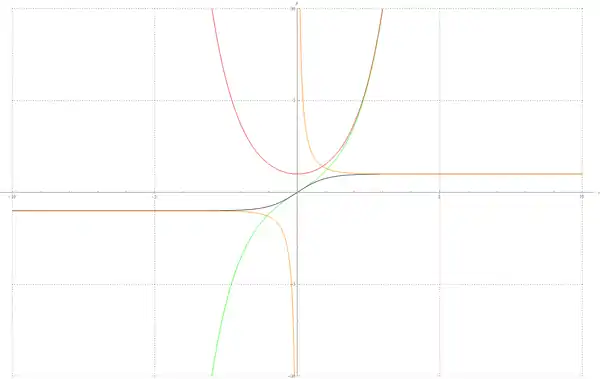
Графіки
Аналітичні властивості
Гіперболічний синус і гіперболічний косинус аналітичний у всій комплексній площині, за винятком істотно особливої точки на нескінченності. Гіперболічний тангенс аналітичний скрізь, окрім полюсів в точках , де — ціле. Лишки у всіх цих полюсах рівні одиниці. Гіперболічний котангенс аналітичний скрізь, окрім точок , лишки в цих полюсах також рівні одиниці.
Див. також
Посилання
- Гіперболічні функції // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 184. — 594 с.
- Гиперболические функции - sh, ch, th, cth, sech, csch. www.math10.com. Процитовано 20 липня 2021. (рос.)
