Еліптична орбіта
В астродинаміці або небесній механіці, еліптичною орбітою є орбіта Кеплера із ексцентриситетом меншим за 1; що також включає окремий випадок колової орбіти, що має ексцентриситет рівний 0. В більш суворому сенсі, це орбіта Кеплера із ексцентриситетом більшому за 0 і меншому за 1 (таким чином виключаючи колову орбіту). В ширшому розумінні, це Кеплерова орбіта з від'ємною енергією. Таким чином включає радіальну еліптичну орбіту із ексцентриситетом, що дорівнює 1.
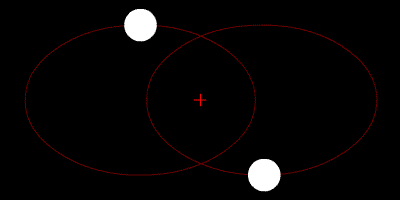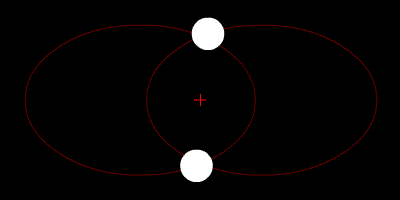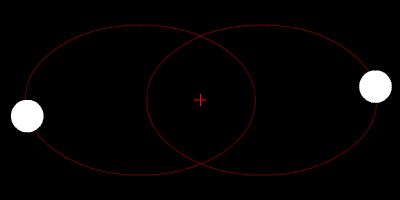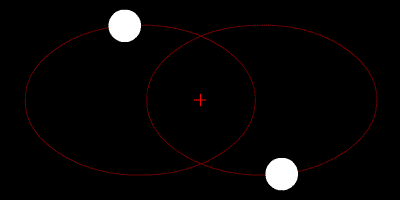
Швидкість
Згідно стандартних припущень орбітальна швидкість () тіла, що подорожує еліптичною орбітою можна розрахувати із рівняння орбітально-енергетичної інваріантності наступним чином:
де:
- — стандартний гравітаційний параметр,
- — відстань між орбітальними тілами.
- — довжина великої півосі.
Орбітальний період
Орбітальний період () руху тіла здовж еліптичної орбіти можна розрахувати наступним чином:
де:
- — стандартний гравітаційний параметр,
- — довжина великої півосі.
Висновки із рівняння:
- Орбітальний період дорівнює періоду колової орбіти із орбітальним радіусом, що дорівнює великій півосі (),
- Для заданої великої півосі орбітальний період не залежить від ексцентриситету (див. також: Третій закон Кеплера).
Енергія
Питома енергія орбіти () еліптичної орбіти має від'ємне значення і рівняння збереження орбітальної енергії (рівняння орбітально-енергетичної інваріантності) для такої орбіти матиме наступну форму:
де:
- — орбітальна швидкість орбітального тіла,
- — відстань орбітального тіла від центрального тіла,
- — довжина великої півосі,
- — стандартний гравітаційний параметр.
Висновок:
- Для заданої великої півосі питома орбітальна енергія не залежить від ексцентриситету.
Використавши теорему віріалу можна знайти:
- середнє за часом значення питомої потенційної енергії дорівнює −2ε
- середнє за часом значення r−1 становить a−1
- середнє за часом значення питомої кінетичної енергії дорівнює ε
Сонячна система
В Сонячній системі, планети, астероїди, і більшість комет і деякі уламки Космічного сміття обертаючись довкола Сонця мають орбіти близькі до еліптичних. Строго кажучи, обидва тіла обертаються довкола одного фокусу еліпсоїда, один з низ ближчий до найбільш масивного тіла, але коли одне із тіл значно масивніше, так як Сонце в порівнянні з Землею, фокус знаходиться в середині більшого масивного тілаy, і таким чином кажуть, що менше тіло обертається довкола нього. Наступна діаграма перигелію і афелію планет, карликових планет і Комети Галлея показує мінливість ексцентриситету їх еліптичних орбіт. Для однакових відстаней від Сонця, більш широкі смуги означають більший ексцентриситет. Варто відмітити майже нульовий ексцентриситет Землі і Венери в порівнянні з величезна ексцентричність комети Галлея і Ериди.
Історія
Вавилонці були першими хто зрозумів, що рух Сонця по екліптиці не є рівномірним, хоча вони і не змогли пояснити чому це так; сьогодні відомо, що це тому що Земля обертається довкола Сонця по еліптичній орбіті, і Земля рухається швидше коли знаходиться ближче до Сонця в перигелії і рухається повільніше коли знаходиться далі в афелії.[1]
В 17-му столітті, Йоганн Кеплер відкрив, що орбіти по яким планети рухаються довкола Сонця є еліпсами і Сонце знаходиться в одному з фокусів, і описав це як Перший закон руху планет. Згодом, Ісаак Ньютон пояснив це як наслідок відкритого ним закону всесвітнього тяжіння.
Посилання
- JAVA applet animating the orbit of a satellite in an elliptic Kepler orbit around the Earth with any value for semi-major axis and eccentricity.
- Apogee — Perigee Lunar photographic comparison
- Aphelion — Perihelion Solar photographic comparison
- http://www.castor2.ca
Примітки
- David Leverington (2003). Babylon to Voyager and beyond: a history of planetary astronomy. Cambridge University Press. с. 6–7. ISBN 0-521-80840-5.
