Задача пакування рюкзака

Задача про пакування рюкзаку досліджується вже понад століття. Відома згадка ще 1897 року в статті Джорджа Метьюза Балларда[1]. Сама назва «задача про пакування рюкзаку» відсилає до ранніх робіт математика Тобіаса Данцига (1884—1956)[2], і стосується звичайної проблеми пакування найбільш цінних або корисних речей без перевантаження.

Інтенсивне дослідження проблеми почалось з середини ХХ століття і в 1972 році була включена Річардом Карпом (англ. Richard Karp) до списку 21 NP-повної задачі[3].

Дослідження 1998 року проведене репозитарієм алгоритмів університету Стоні Брук показало, що з 75 алгоритмічних задач, задача пакування рюкзака була 19-ю за по популярністю і 3-ю з найбільш необхідних після таких задач, як суфіксне дерево та задача про пакування в ємності[4].

Задачу пакування рюкзака використовують для моделювання різних проблем, зокрема:

• У системах підтримки управління портфелем для балансування та диверсифікації вибраних капіталовкладень із метою пошуку найкращого балансу між ризиками та ефективністю вкладів у різні фінансові активи[5] та для сек'юритизації активів[6];
• Генерування ключів для криптосистем Меркле — Геллмана[7] та інших криптосистем.

Також задача пакування рюкзака виникає у великій кількості промислових задач[8][9]:

• У кроєнні різних матеріалів (тканини, сталеві листи тощо): вибір оптимальної схеми розкрою матеріалів з метою зменшення кількості відходів[10];
• При завантаженні човна або літака: вибір багажів для оптимального завантаження транспортного засобу;
• При розміщенні вантажів на складі мінімальної площі.

Одним із перших застосувань алгоритмів пакування рюкзака була створення та оцінка тестів, в яких тестовані особи мали вибір, на які питання вони будуть відповідати. При невеликій кількості прикладів це доволі прозорий процес. Наприклад, якщо іспит містить 12 запитань кожен з яких на 10 балів, тестованій особі потрібно відповісти лише на 10 запитань для досягнення максимально можливої оцінки — 100 балів. Проте, якщо тестові завдання дають різну кількість балів, зробити вибір вже важче. Фюерман і Вайс запропонували систему, в якій студентам дають гетерогенний тест із загальною кількістю 125 можливих балів. Студентів просять відповісти на всі питання, наскільки це можливо. З усіх можливих підмножин завдань, загальні значення яких дорівнюють або не перевищують 100, алгоритм визначає, який піднабір дасть кожному студенту найвищий можливий бал[11].

Задачу пакування рюкзака можна визначити засобами математичного апарату. Нехай кожному об'єктові для пакування зіставлено індекс i, який приймає значення від 1 до n. Числа ${\displaystyle w_{i}}$ та ${\displaystyle p_{i}}$ відповідають вазі та вартості об'єкта i. Максимальна припустима маса, яку здатен витримати рюкзак, дорівнює W.

0-1 задача пакування рюкзака

Існує багато варіантів заповнення рюкзака. Для описання окремого варіанту пакування необхідно вказати для кожного об'єкта, чи його обрано (запаковано). Для цього можна використати двійковий вектор ${\displaystyle X=(x_{1},x_{2},\dots ,x_{n})}$, компонента ${\displaystyle x_{i}}$ якого дорівнюватиме 1, якщо i-тий об'єкт запаковано, та 0 якщо ні. Цей вектор називається вектором заповнення. Вагу та вартість запакованих предметів, можна обчислити як функцію від вектора заповнення.

Для заданого вектора заповнення X вартість предметів запакованих у рюкзак дорівнює:

${\displaystyle z(X)=\sum _{\{i,\,x_{i}=1\}}p_{i}=\sum _{i=1}^{n}x_{i}p_{i}}$

Аналогічно, загальна маса предметів дорівнює:

${\displaystyle w(X)=\sum _{i=1}^{n}x_{i}w_{i}}$

Таким чином, задача пакування рюкзака полягає у відшуканні такого вектора заповнення ${\displaystyle X=(x_{1},x_{2},\dots ,x_{n})}$, що максимізує функцію ${\displaystyle z(X)}$ за умови:

${\displaystyle w(X)=\sum _{i=1}^{n}x_{i}w_{i}\leqslant W}$ (1)

Тобто, загальна маса обраних предметів ${\displaystyle w(X)}$ не перевищує можливості рюкзака ${\displaystyle W}$.

Взагалі, діють такі додаткові умови:

• ${\displaystyle \sum _{i=1}^{n}w_{i}>W}$: всі доступні об'єкти не можливо покласти до рюкзака разом;
• ${\displaystyle p_{i}>0,\forall i\in \{1,\dots ,n\}}$ : будь-який додатковий об'єкт надає перевагу;
• ${\displaystyle w_{i}>0,\forall i\in \{1,\dots ,n\}}$ : будь-який об'єкт використовує ресурси.

Термінологія:

• Функція ${\displaystyle z(X)}$ — називається цільовою;
• Будь-який вектор ${\displaystyle X}$, що відповідає умові (1), називається припустимим;
• Якщо вартість ${\displaystyle z(X)}$ максимальна, то вектор ${\displaystyle X}$ називається оптимальним.

Припустімо, окрім вартості предмети мають ще одну характеристику (наприклад, щільність). Задача пошуку вектора заповнення ${\displaystyle X}$, що максимізує обидві функції (сумарна вартість та сумарна щільність) є багатокритеріальним варіантом 0-1 задачі пакування рюкзака.[12]

Обмежена задача пакування рюкзака обмежує кількість ${\displaystyle x_{i}}$ копій кожного виду предмета максимальним цілим значенням ${\displaystyle k_{i}}$. Математично цю задачу можна сформулювати так:

• максимізувати ${\displaystyle \qquad \sum _{i=1}^{n}p_{i}x_{i}}$
• за умови ${\displaystyle \qquad \sum _{i=1}^{n}w_{i}x_{i}\leqslant W,\quad \quad x_{i}\in \{0,1,\ldots ,k_{i}\}}$

Необмежена задача пакування рюкзака (НЗПР) не накладає верхньої межі для кількості копій кожного виду предмета. Тобто потрібно

• максимізувати ${\displaystyle \qquad \sum _{i=1}^{n}p_{i}x_{i}}$
• за умови ${\displaystyle \qquad \sum _{i=1}^{n}w_{i}x_{i}\leqslant W,\quad \quad x_{i}\in \{0,1,\ldots \}}$

Приклад такої задачі наведена на малюнку у вступній частині (див. текст «Якщо доступна достатня кількість екземплярів кожної коробки…»)

Особливий інтерес представляє окремий випадок задачі пакування рюкзака з такими властивостями:

• вона є проблемою вибору,
• вона є 0-1 задачею,
• для кожного виду предмета вага дорівнює вартості: ${\displaystyle w_{i}=p_{i}}$.

У цьому разі задача еквівалентна такій задачі: задано множину невід'ємних цілих чисел, чи існує будь-яка її підмножина, сума елементів якої складає точно W? Або, якщо допускається від'ємна вага і W дорівнює нулю, то задачею є: задано множину цілих чисел, чи існує непорожня підмножина, сума елементів якої точно дорівнює 0? Цей окремий випадок називається задачею суми підмножини. У галузі криптографії термін задача пакування рюкзака часто використовується для позначення конкретно задачі суми підмножини.

Якщо допускається декілька рюкзаків, то задачу краще розглядати як задачу пакування в ємності.

Як і для інших NP-повних задач, в деяких випадках достатньо знайти рішення, наближене до оптимального, але не обов'язково оптимальне. Бажано, також, щоб різниця між оптимальним розв'язком та знайденим була гарантованих розмірів.

Далі під ефективністю предмета розуміється відношення його вартості до ваги. Чим вище ефективність предмета, тим кориснішим він є для пакування.

Жадібний алгоритм

Дві фази жадібного алгоритму: Ліворуч: впорядкування предметів за їхньою ефективністю (в цьому разі, вартість на кіло ваги). Праворуч: пакування в рюкзак, якщо є можливість. Отриманий розв'язок дає $11 та 11 кг, в той час як оптимальний $12 та 14 кг.

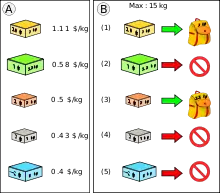
Одним з найпростіших алгоритмів пошуку приблизного розв'язку є жадібний алгоритм. Ідея алгоритму полягає в тому, щоб класти до рюкзака в першу чергу найефективніші предмети, аж до його заповнення:

 впорядкувати предмети у порядку зменшення ефективності
 w_пак: = 0

 для i від 1 до n
   якщо w[i] + w_пак <= W тоді
     x[i] := 1
     w_пак := w_пак + w[i]
   інакше
     x[i] := 0
   кінець якщо
 кінець для

Класична задача пакування рюкзака була вивчена досить глибоко. Існує багато методів пошуку точних розв'язків задачі. Більшість з них є покращеними варіантами одного з наведених нижче методів пошуку точного розв'язку задачі. А саме використовується підхід динамічне програмування[15], метод гілок і меж[16] або гібридне поєднання обох підходів.[17][18][19][20]

для c від 0 до W робити
  T[0,c] := 0
кінець для

для i від 1 до n робити
  для c від 0 до W робити
    якщо c>=w[i] то
      T[i,c] := max( T[i-1,c], T[i-1, c-w[i]] + p[i] )
    інакше
      T[i,c] := T[i-1,c]
    кінець якщо
  кінець для
кінець для
вивести T[n,W]

• Hans Kellerer, Ulright Pferschy and David Pisinger, Knapsack Problems, Springer, 2004 ISBN 3-540-40286-1. (англ.)
• Honsberger, R. Mathematical Gems III. Washington, DC: Math. Assoc. Amer., pp. 163—166, 1985. (англ.)

• Список задач про наповнення рюкзака
• 21 NP-повна задача Карпа
• Комбінаторна оптимізація
• Задача про пакування в ємності
• Задача комівояжера

• Динамічне програмування. 0-1 задача пакування рюкзака (слайди лекції) (англ.)
• Слайди лекції з динамічного програмування (п.4. Задача пакування рюкзака). (рос.)