Теорія множин

Георг Кантор (1845—†1918), фундатор теорії множин

До другої половини 19 століття поняття «множини» не розглядалося як математичне («множина книг на полиці», «множина людських чеснот» і т. д. — все це суто побутові мовні звороти). Становище змінилося, коли німецький математик Георг Кантор розробив свою програму стандартизації математики, в рамках якої будь-який математичний об'єкт мав бути тією або іншою «множиною». Цей підхід викладений у двох його статтях, опублікованих у 1879—1897 роках у відомому німецькому журналі «Mathematische Annalen»[1][2].

Наприклад, натуральне число за Кантором слід було розглядати як множину, що складається з єдиного елемента іншої множини, званої «натуральним рядом», який, у свою чергу, сам є множиною, що задовольняє так званим аксіомам Пеано.

При цьому загальному поняттю «множини», що розглядалося ним як центральне для математики, Кантор давав вельми розмиті означення, ніби «множина є багато що, мислиме як єдине», і т. д. Це цілком відповідало наміру самого Кантора, який підкреслено називав свою програму не «теорією множин» (цей термін з'явився багато пізніше), а «вченням про множини» (Mengenlehre).

Програма Кантора викликала різкі протести з боку багатьох сучасних йому відомих математиків. Особливо виділявся своїм непримиренним до неї ставленням Леопольд Кронекер, який вважав, що математичними об'єктами можуть вважатися лише натуральні числа і те, що до них безпосередньо зводиться (відома його фраза про те, що «бог створив натуральні числа, а все інше — справа рук людських»).

Повністю відкинули теорію множин і такі авторитетні математики, як Герман Шварц та Анрі Пуанкаре. Проте, деякі інші математики — зокрема, Готлоб Фреге, Ріхард Дедекінд та Давид Гільберт — підтримали Кантора в його намірі перекласти всю математику на теоретико-множинну мову. Зокрема, теорія множин стала основою: теорії міри, топології, функціонального аналізу.

Проте незабаром з'ясувалося, що спрямування Кантора на відсутність обмежень при операціях з множинами (виражене ним самим у принципі «суть математики полягає в її свободі») недосконала із самого початку; а саме, було знайдено ряд теоретико-множинних антиномій: виявилося, що при використанні теоретико-множинних уявлень деякі твердження можуть бути доведені разом зі своїми запереченнями (а тоді, відповідно до правил класичної логіки висловлень, може бути «доведено» абсолютно будь-яке твердження). Першою такою антимонією став парадокс Буралі-Форті, відкритий самим Кантором ще в 1895 році[3][4], що показував, що припущення про існування множини всіх порядкових чисел веде до протиріччя. Пізніше було відкрито велику кількість парадоксів, пов'язаних з самореференціями, наприклад, парадокс Расселла виникає при спробі побудувати множину всіх множин, що не містять себе як свого елемента. Подібним же способом формулюються Парадокс Ґреллінґа — Нельсона і Парадокс Беррі. Трохи інакше побудований парадокс Рішара, що має семантичну природу.

Антиномії ознаменували собою повний провал програми Кантора.

Ернст Цермело (1871—†1953), автор аксіоматики теорії множин

В 1901 році Бертран Расселл, вивчаючи наївну теорію множин, дійшов до парадоксу (відтоді відомому як парадокс Рассела). Таким чином була продемонстрована суперечливість наївної теорії множин і, пов'язаної з нею канторівської програми стандартизації математики. Аксіоматична теорія множин була початково розроблена, щоб позбутися таких парадоксів в теорії множин.[5]

Після виявлення антиномії Рассела частина математиків (наприклад, Л. Е. Я. Брауер і його школа) вирішила повністю відмовитися від використовування теоретико-множинних уявлень.

Інша ж частина математиків, очолена Давидом Гільбертом здійснила низку спроб обґрунтувати ту частину теоретико-множинних уявлень, яка здавалася їм якнайменше відповідальною за виникнення антиномій, на основі надійної фінітної математики.

Сам Кантор, усвідомивши ці проблеми, запропонував ввести поняття «консистентності», яку він характеризував як можливість уявити множину як одне ціле, і з її допомогою розділити власне множини, і «множинності» — більш складні конструкції, що не мають цієї властивості.[6]. Ця ідея, хоча і не увійшла до аксіоматичної теорії безпосередньо, проте вплинула на подальші дослідження, і, в більш формалізованому вигляді була реалізована.

Логічний апарат удосконалив Бертран Рассел в роботах, пізніше зібраних у його монографії «Principia Mathematica» (1910—1913). І в 1904—1908 роках Ернст Цермело запропонував першу із аксіоматичної теорії множин.

Особливістю аксіоматичного підходу є відмова від закладеного у програму Кантора уявлення про справжнє існування множин в деякому ідеальному світі. У рамках аксіоматичних теорій множини «існують» винятково формальним чином, і їх «властивості» можуть істотно залежати від вибору аксіоматики. Цей факт завжди був мішенню для критики з боку тих математиків, які не згоджувалися (як на тому наполягав Гільберт) визнати математику, позбавленою будь-якого змісту, грою в символи. Зокрема, М. М. Лузін писав, що «потужність континууму, якщо тільки мислити його як множина точок є якась єдина реальність», місце якої в ряду кардинальних чисел не може залежати від того, чи визнається як аксіома континуум-гіпотеза, чи її заперечення.

Наразі найпоширенішою аксіоматичною теорією множин є ZFC — теорія Цермело-Френкеля з аксіомою вибору. Питання про несуперечність цієї теорії (а тим більше — про існування моделі для неї) залишається нерозв'язаним.

Діаграма Венна, що демонструє множини великих літер грецької, латинської і російської мови

• Кола Ейлера і їх окремий випадок, діаграми Ейлера-Вена — широко використовуються для того, щоб позначити прості відношення між скінченною кількістю множин. Самі множини при цьому можуть бути як скінченними, так і нескінченними. Деякі теореми теорії множин стають очевидними після побудови відповідної діаграмми. На практиці є зручними лише для невеликої кількості множин.
• Квантори загальності (${\displaystyle \forall }$) і існування (${\displaystyle \exists }$) — є скороченим записом фраз «для будь-якого об'єкту вірно, що …» і «існує принаймні один об'єкт, такий що …». Також ці позначення мають назви універсальний і екзистенційний квантор.
• Індексні позначення — використовуються для перерахування елементів множини, тобто, якщо є множина ${\displaystyle A}$, то її елементи, зазвичай, позначають як ${\displaystyle a_{1},a_{2},a_{3}...}$.

В основі теорії множин лежать первинні поняття: множина та елемент множини. Елемент множини перебуває щодо множини у відношенні бути елементом множини (позначається як ${\displaystyle x\in A}$[7] — «x є елемент множини A»). Серед похідних понять важливими є поняття підмножини і надмножини — множина, яка складається тільки з елементів іншої множини, та множина, до якої належать усі елементи іншої множини, відповідно. Як видно з цього визначення, будь-яка множина є власною підмножиною і надмножиною. Підмножина, що не збігається з множиною, підмножиною якої вона є, і не є порожньою, називається власною, або нетривіальною підмножиною. Множини вважаються рівними, якщо всі їх елементи збігаються (або ж, інакше, кожна з них є підмножиною другої). Ці відношення позначаються наступним чином:

• Відношення включення (позначається як ${\displaystyle A\subset B,}$ або ${\displaystyle A\subseteq B}$).
• Відношення рівності (позначається як ${\displaystyle A=B\,}$);

Над множинами визначені наступні операції:

• Об'єднання (або сума) (позначається як ${\displaystyle \ A\cup B}$) — множина, що містить всі об'єкти, які є елементами принаймні однієї з множин А і В;
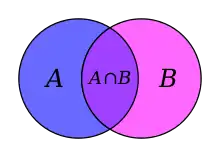
• Перетин (або добуток) (позначається як ${\displaystyle \ A\cap B}$) — множина, що містить всі об'єкти, які є елементами одночасно множини А і множини В;
• Різниця (позначається як ${\displaystyle \ A\setminus B,}$ рідше ${\displaystyle \ A-B}$) — множина, що містить всі об'єкти, які є елементами множини А, але не є елементами множини В;
• Симетрична різниця (позначається як ${\displaystyle A\,\triangle \,B,}$ рідше ${\displaystyle A\,{\dot {-}}\,B}$) — множина, що містить всі об'єкти, які є елементами множини А або множини В, але не їх обох.

• Базові операції з множинами
• 
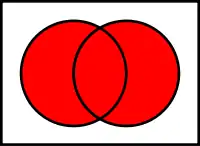  Об'єднання множин A та B
• 
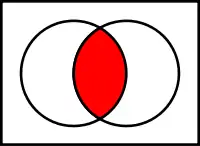  Перетин множин A та B
• 
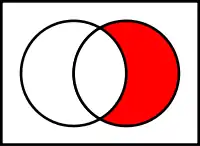  Різниця B і A
• 
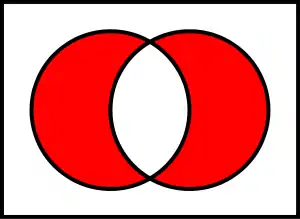  Симетрична різниця A та B

• Доповнення (позначається як ${\displaystyle \ \setminus A,}$ або ${\displaystyle -A\,}$) — множина всіх об'єктів, що не є елементами множини А;
• Декартів добуток множин ${\displaystyle \scriptstyle A\times B}$ — множина всіх можливих впорядкованих пар ${\displaystyle (a,b)}$, таких що ${\displaystyle a\in A,b\in B}$. Наприклад, добутком множин {1, 2} і {а, б, в} буде {(1, а), (1, б), (1, в), (2, а), (2, б), (2, в)}
  • Підмножина декартового добутку називається бінарним відношенням між множинами. Наприклад, відношення «ділиться на» між множинами {2, 5, 8} і {2, 4, 7} є множиною {(2, 2), (8, 2), (8, 4)}, яка є підмножиною їх декартового добутку;
  • Проєкцією елементу ${\displaystyle (a,b)\in R\subseteq A\times B}$ на множину ${\displaystyle A}$ називають елемент ${\displaystyle a\in A}$[8]
  • Перерізом відношення ${\displaystyle R\subseteq A\times B}$ по деякому елементу ${\displaystyle a\in A}$, є підмножина ${\displaystyle Y}$ множини ${\displaystyle B}$, така, що для всіх елементів ${\displaystyle y}$ цієї підмножини ${\displaystyle (a,y)\in R}$. Іноді такий переріз називають верхнім перерізом, а аналогічну конструкцію для другої множини — нижнім перерізом[9]
  • Оберненим відношенням до відношення ${\displaystyle R\subseteq A\times B}$ називається відношення ${\displaystyle R^{-1}}$, таке, що для будь-яких ${\displaystyle a\in A,b\in B:bR^{-1}a=aRb}$[10]
  • Функціональним відношенням називають таке відношення ${\displaystyle R\subseteq A\times B}$, де будь-якому ${\displaystyle a\in A}$ відповідає не більш ніж одна пара (a, b)[11]
  • Взаємно-однозначним відношенням називається функціональне відношення, обернене до якого також є функціональним.

Схема доведення рівнопотужності раціональних і натуральних чисел

• Булеан множини — множина всіх підмножин деякої множини. Позначається ${\displaystyle {\mathcal {P}}(A)}$ або ${\displaystyle 2^{A}}$. Наприклад, булеаном множини {1, 2} буде {{}, {1}, {2}, {1, 2}}
• Потужність множини, або кардинальне число — характеристика, що є узагальненням поняття кількості елементів. Власне, для скінченних множин їхня потужність дорівнює кількості їхніх елементів. Нескінченні множини утворюють свою ієрархію. Множини вважаються рівнопотужними, якщо між їхніми елементами можна встановити взаємнооднозначну відповідність. Потужність позначається як ${\displaystyle |A|}$, ${\displaystyle {\overline {\overline {A}}}}$, ${\displaystyle \#A}$ або ${\displaystyle \mathrm {card} (A)}$.

Серед важливих множин можна назвати:

• Порожня множина — множина, яка не містить елементів, позначається зазвичай ${\displaystyle \varnothing }$. Порожня множина є підмножиною будь-якої множини;
• Простір (універсум) — множина, що є надмножиною всіх множин (не варто плутати це поняття з множиною всіх множин, існування якої призводить до парадоксів);
• Множина натуральних чисел — позначається літерою ${\displaystyle \mathbb {N} }$. Найменша з нескінченних множин. Множини, потужність яких рівна потужності множини натуральних чисел називаються зліченними.
• Множина дійсних чисел — позначається літерою ${\displaystyle \mathbb {R} }$. Згідно континуум-гіпотезі, множина дійсних чисел є другою найменш потужною серед нескінченних.

Свого сучасного вигляду набула у 1922 році завдяки роботам Туральфа Скулема і Адольфа Френкеля, що доопрацювали опубліковані в 1908 році Ернстом Цермелло аксіоми. Ця система має скорочену назву ZFC, і є найбільш популярною системою аксіом теорії множин. Її можна сформулювати таким чином:

• Аксіома об'ємності — дві множини є рівними, якщо будь-який елемент, що міститься в першій множині, міститься і в другій, і навпаки;
• Аксіома порожньої множини — існує порожня множина, що не містить жодного елемента;
• Аксіома нескінченності — існує нескінченна множина, що має такі властивості:
  • Ця множина містить порожню множину
  • Якщо ця множина містить деякий елемент b, то вона містить і елемент {b}

Таким чином, така множина має вигляд

${\displaystyle \{\varnothing ,\ \ \varnothing \cup \{\varnothing \},\ \ \varnothing \cup \{\varnothing \}\cup \{\varnothing \cup \{\varnothing \}\},\ \ldots \}}$

• Аксіома пари — якщо існують дві множини ${\displaystyle a_{1}}$ і ${\displaystyle a_{2}}$, то існує множина кожен елемент якої дорівнює або ${\displaystyle a_{1}}$, або ${\displaystyle a_{2}}$ ;
• Аксіома булеана — для будь-якої множини існує множина всіх її підмножин;
• Аксіома об'єднання — для будь-якого набору(родини) множин, можна створити множину, кожен елемент якої належить принаймні до однієї з цих множин;
• Аксіомна схема виділення — якщо є деяке математичне твердження, що може бути застосованним до будь-якого з елементів деякої множини, то можна виділити принаймні одну підмножину цієї множини, застосувавши це твердження;
• Аксіома підстановки — якщо є функціональне відношення, що може бути застосована до кожного з елементів множини, то, застосувавши його, можна визначити нову (або ж таку саму) множину;
• Аксіома регулярності — у будь-якій родині множин існує принаймні одна множина, кожен елемент якої не належить цій родині. Одним з наслідків цієї аксіоми є те, що жодна множина не є елементом самої себе;
• Аксіома вибору — для будь-якого набору непорожніх, неперетинаючихся множин можна побудувати множину, кожен елемент якої є елементом однієї і тільки однієї з множин цього набору.

На відміну від інших, остання аксіома не є достатньо самоочевидною, і тому деякі математики виключають її (система аксіом Цермело — Френкеля без неї позначається просто як ZF). Недовіра до аксіоми вибору підсилюється тим, що наслідки, що випливають з неї, можуть бути дуже контрінтуітивними і парадоксальними, наприклад, процедура Банаха-Тарського, що використовує аксіому вибору, дозводяє розділити тривимірну кулю на п'ять шматків, і зібрати з них дві кулі такого самого розміру.

Система аксіом Неймана — Бернайса — Геделя (NBG) є розширенням ZFC. Поняття, сформульовані в ZFC можуть бути доведені тоді, і тільки тоді, якщо вони можуть бути доведені в NBG.

Була розроблена в період з 1940 по 1954 роки Куртом Геделем і Паулем Бернайсом, і розвивала аксіоматику, розроблену Джоном фон Нейманом у 1926 році.

Вводить поняття власного класу — об'єкту, що має у собі елементи, але сам не може бути елементом ніяких об'єктів. Серед аксіом, що містяться у NBG, але не містяться у ZFC можна назвати такі:

• Аксиома обмеження потужності — для будь-якого класу, множина, що збігається з цим класом, може існувати лише тоді, коли не існує бієкції між цим класом і класом всіх множин.
• Схема аксіом породження підклассів — для будь-якої формули ${\displaystyle \varphi }$, що не містить кванторів для змінних-классів (вона може містити змінні-класи як параметри) існує клас ${\displaystyle A}$, такий, що ${\displaystyle \forall x(x\in A\leftrightarrow \varphi (x))}$.[12]

Комбінаторна теорія множин (нескінченна комбінаторика) розглядає розширення комбінаторики для нескінченних множин. До нього належать дослідження кардинальної арифметики і вивчення розширень теореми Рамзея, таких як теорема Ердеша-Радо[13].

Описова, або дескриптивна теорія множин — вивчає внутрішні властивості множин, що побудовані з об'єктів відносно простої природи — відкритих і замкнених множин евклідових, метричних і топологічних просторів за допомогою теоретико-множинних операцій, таких як об'єднання, перетин, різниця тощо. Простори, що вивчаються дескриптивною теорією множин носять загальну назву польські простори. До таких просторів належать, наприклад, простори ${\displaystyle \mathbb {R} }$ (дійсні числа), ${\displaystyle 2^{\mathbb {N} }}$ (дисконтінуум Кантора), ${\displaystyle \mathbb {N} ^{\mathbb {N} }}$ (берівський простір), ${\displaystyle I^{\mathbb {N} }}$ (Гільбертова цеглина). Серед множин, що вивчаються дескриптивною теорією множин можна назвати борелівські множини, що отримані з відкритих множин вихідного простору не більш ніж зліченною кількістю перетинів, об'єднань і різниць, а також А-множини, введені Александровим, що отримені за допомогою незліченної кількості таких операцій.[14] Найбільший вклад в дескриптивну теорію множин внесли Фелікс Гаусдорф, Микола Лузін, Павло Александров, Михайло Суслін.

Нечіткі множини були введені одночасно[15] Лотфі Заде[16] і Дітером Кляуа[17] в 1965 році як розширення класичного поняття множини. У теорії множин введеній Кантором і аксіоматизованії Цермело і Френкелем, елемент або належить множині, або ні. У теорії нечітких множин цю умову було ослаблено, елемент має ступінь належності до множини, який задається числом між 0 і 1. Наприклад, ступінь приналежності конкретної людини до множини «високих людей» є гнучкішим, ніж просто так чи ні, і може бути дійсним числом, скажімо, 0,75. Теорія розмитих множин визначена Лотфі Заде використовується в лінгвістиці. Заде вказує на те що деякі категорії не мають ступенів членування тоді як в інших вони є. Категорія сенатор США — чітко визначена. Проте, з іншого боку такі категорії як багаті люди чи високі люди градуйовані лише тому, що є різні ступені багатства та високого росту. Заде запропонував різновид теорії множин для того, щоб моделювати градуйовані категорії. У розмитих множинах за визначенням Заде допускається додаткове значення між 0 і 1.