Задача про максимальний потік
В теорії оптимізації та теорії графів, задача про максимальний потік полягає у знаходженні такого потоку за транспортною мережею, щоб сума потоків з витоку, або, що означає те ж саме, сума потоків до стоку була максимальна.
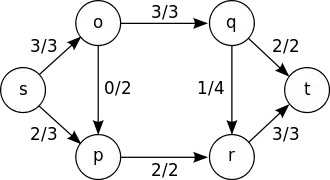
Задача про максимальний потік є окремим випадком більш складних задач, таких, як, наприклад, задача про циркуляцію.
Історія
Після вступу США у Другу світову війну у 1941 році математик Джордж Бернард Данціг почав працювати у відділі статистичного управління Військово-повітряних сил США у Вашингтоні. З 1941 по 1946 роки він очолював підрозділ аналізу військових дій (Combat Analysis Branch), де працював над різноманітними математичними проблемами.[1][2] Згодом з використанням роботи Данцига задача про максимальний потік була вперше розв'язана у ході підготовки повітряного мосту під час Берлінського повітряного мосту, що відбувався у 1948–1949 роках.[3][4][5]
У 1951 році Джордж Данциг вперше сформулював задачу у загальному вигляді.[6]
У 1955 році Лестер Форд і Делберт Фалкерсон вперше побудували алгоритм, призначений для вирішення цього завдання. Їх алгоритм отримав назву алгоритм Форда — Фалкерсона.[7][8]
Надалі рішення задачі багато разів поліпшувалося.
У 2010 році дослідники Джонатан Келнер (Jonathan Kelner) і Олександр Мондри (Aleksander Mądry) з МТІ разом зі своїми колегами Даніелєм Спілманом з Єльського університету і Шень-Хуа Тенем з університету Південної Каліфорнії продемонстрували чергове покращення алгоритму, вперше за 10 років.[3][9][10]
Визначення
Розглянемо транспортну мережу з джерелом , стоком та пропускними здатностями .
- Величиною потоку (value of flow) називається сума потоків з джерела . У статті «Транспортна мережа» доведено, що вона дорівнює сумі потоків у сток .
Задача про максимальний потік полягає в знаходженні потоку такого, щоб величина потоку була максимальна.
Розв'язання
В таблиці перераховано деякі алгоритми розв'язування задачі.
| Метод | Складність | Опис |
|---|---|---|
| Лінійне програмування | Залежить від конкретного алгоритму. Для симплекс-методу експоненціальна. |
Розглянемо задачу про максимальний потік як задачу лінійного програмування. Змінними є потоки по ребрах, а обмеженнями — збереження потоку й обмеження пропускної здатності. |
| Алгоритм Форда — Фалкерсона | Залежить від алгоритму пошуку шляху, що збільшується. Потребує O(max| f |) таких пошуків. |
Знайти будь-який шлях, що збільшується. Збільшити потік по всіх його ребрах на мінімальну з їх залишкових пропускних здатностей. Повторювати, поки є шлях, що збільшується. Алгоритм працює тільки для цілих пропускних здатностей. В іншому випадку, він може працювати нескінченно довго, не сходячись до правильної відповіді. |
| Алгоритм Едмондса-Карпа | O(VE²) | Виконуємо алгоритм Форда — Фалкерсона, щоразу обираючи найкоротший шлях, що збільшується (знаходиться пошуком у ширину). |
| Алгоритм Дініца | O(V²E) для одиничних пропускних здатностей з використанням динамічних дерев Слетора і Тар'яна[11] |
Удосконалення алгоритму Едмондса-Карпа (але хронологічно був знайдений раніше). На кожній ітерації, використовуючи пошук у ширину, визначаємо відстані від джерела до всіх вершин у залишковій мережі. Будуємо граф, який містить лише такі ребра залишкової мережі, на яких ця відстань зростає на 1. Виключаємо з графу усі тупикові вершини з інцидентними їм ребрами, поки всі вершини стануть не тупиковими. (Тупиковою називається вершина, в яку не входить і з якої не виходить жодне ребро, крім джерела і стоку.) На отриманому графі відшукуємо найкоротший шлях, що збільшується (їм буде будь-який шлях з s в t). Виключаємо із залишкової мережі ребро з мінімальною пропускною здатністю, знову виключаємо тупикові вершини, і так поки ще існують шляхи, що збільшуються. |
| Алгоритм просовування предпотоку | O(V²E) | Замість потоку оперує з передпотоком. Різниця в тому, що для будь-якої вершини u, крім джерела і стоку, сума потоків, що входять до неї для потоку повинна бути строго нульовою (умова збереження потоку), а для передпотока — невід'ємною. Ця сума називається надмірним потоком у вершину, а вершина з позитивним надмірним потоком називається переповненою . Крім того, для кожної вершини алгоритм зберігає додаткову характеристику, висоту, яка є цілим невід'ємним числом. Алгоритм використовує дві операції: просування , коли потік по ребру, що йде з більш високої в нижчу вершину, збільшується на максимально можливу величину, і підйом , коли переповнена вершина, просування з якої неможливо через недостатню висоту, підіймається. Просування можливо, коли ребро належить залишковій мережі, коли воно веде з більш високої вершини в більш низьку, і вихідна вершина переповнена. Підйом можливий, коли вершина, що піднімається, переповнена, але жодна з вершин, в котру з неї ведуть ребра залишкової мережі, не нижче за неї. Він вчиняється до висоти на 1 більшою, ніж мінімальна з висот цих вершин. Спочатку висота джерела V, по всім ребрам, що виходять з джерела, тече максимально можливий потік, а решта висоти і потоки нульові. Операція просування і підйому виконуються до тих пір, поки це можливо. |
| Алгоритм «підняти на початок» | O(V³) O(VE log(V²/E)) з використанням динамічних дерев |
Варіант попереднього алгоритму, що спеціальним чином визначає порядок операцій просовування і підйому. |
| Алгоритм двiйкового блокуючого потоку |
Теорема про цілий потік
Якщо пропускні спроможності цілі, максимальна величина потоку теж ціла.
Теорема випливає, наприклад, з теореми Форда-Фалкерсона.
Узагальнення, що зводяться до вихідної задачі
Деякі узагальнення задачі про максимальний потік легко зводяться до вихідної задачі.
Довільне число джерел та / або стоків
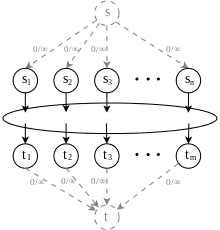
Якщо джерел більше одного, додаємо нову вершину S, яку робимо єдиним джерелом. Додаємо ребра з нескінченною пропускною здатністю від S до кожного зі старих джерел.
Аналогічно, якщо стоків більше одного, додаємо нову вершину T, яку робимо єдиним стоком. Додаємо ребра з нескінченною пропускною здатністю від кожного зі старих стоків до T.
Неорієнтовані ребра
Кожне неорієнтоване ребро (u, v) замінюємо на пару орієнтованих ребер (u, v) і (v, u).
Обмеження пропускної здатності вершин
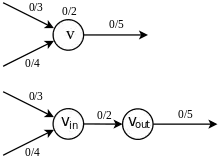
Кожну вершину v з обмеженою пропускною здатністю розщеплюємо на дві вершини vin і vout. Всі ребра, які до розщеплення входять до v, тепер входять в vin. Всі ребра, які до розщеплення виходять з v, тепер виходять з vout. Додаємо ребро (vin,vout) з пропускною здатністю .
Див. також
Примітки
- Джон Дж. О'Коннор та Едмунд Ф. Робертсон. George Dantzig в архіві MacTutor (англ.)
- Cottle, Richard; Johnson, Ellis; Wets, Roger, «George B. Dantzig (1914–2005)», Notices of the American Mathematical Society, v.54, no.3, March 2007. Cf. p.348
- Hardesty, Larry, «First improvement of fundamental algorithm in 10 years», MIT News Office, September 27, 2010
- Borndörfer, Ralf; Grötschel, Martin; Löbel, Andreas, «Alcuin's Transportation Problems and Integer Programing» Архівовано 7 серпня 2011 у Wayback Machine., Konrad-Zuse-Zentrum für Informationstechnik, Berlin, Germany, November 1995. Cf. p.3
- Powell, Stewart M., «The Berlin Airlift», Air Force Magazine, June 1998.
- Dantzig, G.B., «Application of the Simplex Method to a Transportation Problem», in T.C. Koopman (ed.): Activity Analysis and Production and Allocation, New York, (1951) 359–373.
- Ford, L.R., Jr.; Fulkerson, D.R., «Maximal Flow through a Network», Canadian Journal of Mathematics (1956), pp.399-404.
- Ford, L.R., Jr.; Fulkerson, D.R., Flows in Networks, Princeton University Press (1962).
- Kelner, Jonathan, «Electrical Flows, Laplacian Systems and Faster Approximation of Maximum Flow in Undirected Graphs» Архівовано 24 червня 2011 у Wayback Machine., talk at CSAIL, MIT, Tuesday, September 28 2010
- Electrical Flows, Laplacian Systems, and Faster Approximation of Maximum Flow in Undirected Graphs Архівовано 29 листопада 2010 у Wayback Machine., by Paul Cristiano et al., October 19, 2010.
- Алгоритм Диница
Література
- Schrijver, Alexander, «On the history of the transportation and maximum flow problems», Mathematical Programming 91 (2002) 437—445
- Томас Кормен; Чарльз Лейзерсон, Рональд Рівест. Вступ до алгоритмів. MIT Press і McGraw-Hill.. Глава 26. Максимальний потік.
- ↑ Andrew V. Goldberg and S. Rao (1998). Beyond the flow decomposition barrier. J. Assoc. Comput. Mach. 45: 753–782. doi:10.1145/290179.290181.
- ↑ Andrew V. Goldberg and Robert E. Tarjan (1988). A new approach to the maximum-flow problem. Journal of the ACM (New York, New York, U.S.: ACM Press) 35 (4): 921–940. ISSN 0004-5411. doi:10.1145/48014.61051.
- ↑ Joseph Cheriyan and Kurt Mehlhorn (1999). An analysis of the highest-level selection rule in the preflow-push max-flow algorithm. Information Processing Letters 69 (5): 239–242. doi:10.1016/S0020-0190(99)00019-8.
- ↑ Daniel D. Sleator and Robert E. Tarjan (1983). A data structure for dynamic trees. Journal of Computer and System Sciences 26 (3): 362–391. ISSN 0022-0000. doi:10.1016/0022-0000(83)90006-5.
- ↑ Daniel D. Sleator and Robert E. Tarjan (1985). Self-adjusting binary search trees. Journal of the ACM (New York, New York, U.S.: ACM Press) 32 (3): 652–686. ISSN 0004-5411. doi:10.1145/3828.3835.
- Eugene Lawler (2001). 4. Network Flows. Combinatorial Optimization: Networks and Matroids. Dover. с. 109–177. ISBN 0486414531.
