Задача про пакування куль
Задача про пакування куль — задача комбінаторної геометрії про розміщення однакових куль в евклідовому просторі без їх взаємного перетинання. Типова постановка задачі наступна: знайти спосіб розташування куль в просторі, за якого кулі займають найбільшу частину цього простору.
| Задача про пакування куль | |
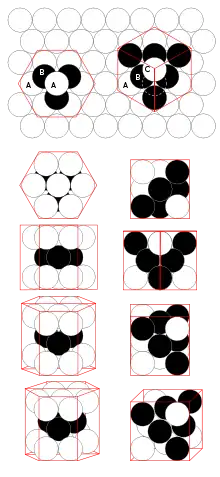 | |
| Попередник | circle packingd |
|---|---|
| | |


Історія задачі
В кінці 1500-х сер Волтер Рейлі попросив англійського математика Томаса Герріота придумати більш ефективний спосіб укладання гарматних ядер на кораблях британського військового флоту. Герріот розповів про це завдання астроному Йогану Кеплеру. Кеплер припустив, що найбільш щільний спосіб упаковки сфер вже і так застосовується — при укладанні гарматних ядер і фруктів: перший шар викладається кулями поруч одна з одною у вигляді шестикутника, другий в заглиблення на стиках куль нижнього шару і т.д. У великій тарі при такому варіанті укладання максимальна щільність буде близько 74%:
Кеплер вважав, що це найщільніший варіант упаковки, але не зміг цього довести. Гіпотезу про найщільніше пакування куль однакових розмірів у тривимірному просторі при їх пірамідальному впорядкуванні одна відносно одної Кеплер виклав в 1611 році в своєму дослідженні «Про шестикутні сніжинки».
В 1694 дискусію щодо пакування куль продовжили Девід Грегорі та Ісаак Ньютон в Кембриджі. Грегорі вважав, що існує таке пакування куль, коли кожна з куль може дотикатись 13 інших, Ньютон обстоював число 12.
Гіпотеза Кеплера залишалася недоведеною протягом декількох століть і потрапила до списку з 23 невирішених математичних задач, складеного у 1900 році Давидом Гільбертом. В 1998 математик Томас Гейлс запропонував складне доведення цієї гіпотези, що базувалось на простому переборі всіх можливих варіантів (варіанти обчислювались за допомогою комп'ютера), але доведення не є математично обґрунтованим[1].
Пакування кіл на площині
У 1940 було доведено, що у двовимірному евклідовому просторі найкращим заповненням є розміщення центрів кіл в вершинах паркету, утвореного правильними шестикутниками, в якому кожне коло оточене шістьма іншими.
Пакування куль у тривимірному просторі
У 1958 математик і популяризатор науки Гарольд Коксетер висловив зауваження, що найщільніше пакування ще не знайдено: 12 куль можна розташувати так, що всі вони будуть дотикатися до центральної кулі, і зовсім трохи не вистачає, щоби до цих 12 можна було додати 13-ту кулю. Порожнечі в розташуванні 12 куль навколо центральної наводять на думку про те, що за певного неправильного пакування щільність може виявитися вищою за 0,74. Можливість такого пакування не доведено, також не доведено, що необхідний дотик з 12 сусідніми кулями.
Гіпотеза Коксетера спонукала проведення ряду експериментів із кулями, упакованими випадковим чином, отримані результати показали, що випадкові упаковки відповідають щільностям у діапазоні від 0,59 до 0,63, що є далеким до 0,74 для щільности впорядкованого пакування.
Пакування в багатовимірних просторах
Пакування на площині та в тривимірному просторі досить легко уявити, але існують також задачі пакування для просторів більшої розмірности.
Задачі для пакування куль у просторі розмірности 8 розв’язала в 2016 році українська математикиня Марина В'язовська[2]. Розв'язок В'язовської для восьмивимірного випадку задачі виявився «приголомшливо простим» — усього 23 сторінки в порівнянні з 300-та сторінками тексту та 50 000 рядків програмного коду під час доведеня гіпотези Кеплера для тривимірного простору.
У 2017 році вона стала співавторкою розв’язку пакування куль в розмірності 24.
Див. також
Примітки
- Компьютер проверил доказательство гипотезы Кеплера (рос.)
- Knudson, Kevin (29 березня 2016). Stacking Cannonballs In 8 Dimensions. Forbes.
Посилання
- Яськов Г. Н. Упаковка большого числа конгруэнтных шаров в цилиндре[недоступне посилання з серпня 2019] (рос.)