Закон випромінювання Планка
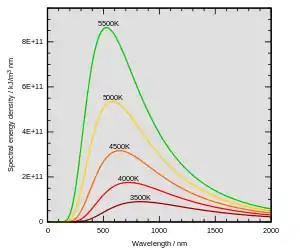
Формула Планка — вираз для спектральної густини потоку випромінювання (спектральної густини енергетичної світності) абсолютно чорного тіла, виведений Максом Планком для густини енергії випромінювання :
Формула Планка («форма» залежності від частоти та температури) спершу була «виведена» емпірично. Формула Планка була отримана після того, як стало зрозуміло, що формула Релея—Джинса, що походить з класичної теорії електромагнітного поля, задовільно описує випромінювання тільки в області довгих хвиль. Зі спаданням довжин хвиль формула Релея—Джинса сильно розходиться з емпіричними даними. Більш того, у граниченому випадку коротких хвиль вона дає розбіжність — нескінчену енергію випромінювання (ультрафіолетова катастрофа).
У зв'язку з цим Планк у 1900 році зробив припущення що суперечить класичній фізиці про те, що електромагнітне випромінення випромінюється у вигляді окремих порцій енергії (квантів), величина яких пов'язана з частотою випромінювання виразом:
Коефіціент пропорційності згодом назвали сталою Планка, = 1,054 · 10−27 ерг·с. Це припущення дозволило пояснити спостережуваний спектр випромінювання теоретично.
Правильність формули Планка підтверджується не тільки емпіричною перевіркою, але й наслідками з даної формули, зокрема з неї походить закон Стефана-Больцмана, також підтверджений емпірично. Крім того, з неї виводяться також приблизні формули, отримані до формули Планка, — формула Віна та формула Релея-Джинса.
Вивід для абсолютно чорного тіла
У наслідок лінійності рівнянь електромагнітного поля будь-який їх розв'язок може бути надано у вигляді суперпозиції монохроматичних хвиль, кожна з певною частотою . Енергія поля може бути представлена як сума енергій відповідних польових осциляторів. Як відомо із квантової механіки, енергія осцилятора приймає дискретні значення згідно з наступної формулою:
Оскільки розглядається рівноважне випромінювання, то використовуючи канонічний розподіл Ґіббса, можна визначити ймовірність стану осцилятора з заданою енергією:
Статистична сума дорівнює
Вільна енергія дорівнює
Для середньої (математичне очікування) енергії скористаємося рівнянням Ґіббса—Гельмгольца
Таким чином, середня енергія, що припадає на польовий осцилятор, дорівнює
| (1) |
де — стала Планка, — стала Больцмана.
Кількість же стоячих хвиль в одиниці об'єму у тривимірному просторі в інтервалі від дорівнює[1][2]:
| (2) |
Отже, для спектральної щільності потужності електромагнітного випромінювання отримуємо:
Перший доданок у цій формулі пов'язаний з енергією нульових коливань, другий являє собою формулу Планка.
Формулу Планка також можна записати через довжину хвилі:
| (5) |
Вивід із розподілу Бозе-Ейнштейна
Фотони є бозонами й підпорядковуються статистиці Бозе — Ейнштейна. Для цієї статистики середнє число частинок із даною енергією дорівнює
Згідно з визначенням,
де — число осциляторів (в одиниці об'єму) електромагнітного поля з даною енергією у нескінченно малому околі .
Підставивши формулу середнього числа бозонів с даною енергією в цю формулу, отримаємо формулу Планка.
Перехід до формул Релея—Джинса
Формула Планка точно узгоджується з експериментальними даними у всьому інтервалі частот від 0 до . При малих частотах, коли можна розкласти експоненту по . У результаті отримаємо, що , тоді (1) і (2) переходять в формулу Релея—Джинса.
- і
Перехід до закону Стефана — Больцмана
Для енергетичної світності слід записати інтеграл:
Введемо змінну , тоді , , отримаємо
Отриманий інтеграл зводиться до дзета-функції Рімана, і має точне значення . Підставивши його, отримаємо відомий закон Стефана — Больцмана:
Підстановка чисельних значень констант дає значення для Вт/(м2 K4), що добре узгоджується з експериментом.
Перехід до закону зміщення Віна
Для переходу до закону Віна, необхідно продиференціювати вираз (5) по та прирівняти похідну нулю (пошук екстремуму):
- .
Значення , при якому функція досягає максимуму, перетворює на нуль вираз, що стоїть у фігурних дужках. Означимо , та отримаємо рівняння:
- .
Розв'язок такого рівняння дає x=4,96511.Отже, , звідси виходить:
- .
Чисельна підстановка констант дає значення для b=0,0028999 К·м, що збігається з експериментальним, а також зручну наближену формулу мкм·К. Так, сонячна поверхня має максимум інтенсивності у зеленій області (0,5 мкм), що відповідає температурі близько 6000 К.
Див. також
Примітки
- Сивухін Д. В. — Москва, 1980. — Т. Том 4 (Оптика). § 117, Формула Релея — Джинса, формула 117.7, с. 692—694(рос.)
- Савельев И. В. — М.: , 1967. — Т. III. Оптика, атомная физика, элементарные частицы. — 416 с.,. Курс общей физики. — Москва : Наука, 1967. — Т. III. — 416 с. § 52, Формула Рэлея — Джинса, формула 52.7, с. 253—258(рос.)
Література
- Планк М. Об одном улучшении закона излучения Вина. Избранные научные труды. Русский пер. из сборника под ред. А. П. Виноградова, стр.249
- Планк М. К теории распределения энергии излучения нормального спектра. Избранные научные труды. Русский пер. из сборника под ред. А. П. Виноградова, стр. 251