Конфігурація Кремони — Річмонда

Конфігурація Кремони — Річмонда — конфігурація з 15 прямих і 15 точок, по три точки, що лежать на кожній прямій, і через кожну точку проходять 3 прямих, при цьому конфігурація не містить трикутників. Конфігурацію вивчали Кремона (Cremona, 1877) і Річмонд (Richmond, 1900). Конфігурація є узагальненим чотирикутником з параметрами (2,2). Граф Леві конфігурації — це граф Татта — Коксетера.[1]

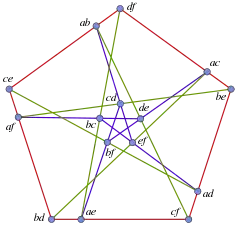
Симетрія

Точки конфігурації Кремони — Річмонда можна ототожнити з $15={\binom {6}{2}}$ невпорядкованими парами елементів множини з шести елементів, прямі ж конфігурації можна ототожнити з 15 способами розкладання цих шести елементів на три пари, при цьому точка інцидентна прямій (лежить на прямій) тоді й лише тоді, коли відповідна пара елементів міститься в розкладі, відповідному прямій. У цій схемі пари елементів називають двійками (duads), а розклади на три пари називаються наборами (synthemes). Таким чином, симетрична група шести елементів діє транзитивно на прапори конфігурації, де прапор — це пара-пряма і точка на ній. Ця група є групою автоморфізмів конфігурації.[1]

Конфігурація Кремони — Річмонда є самодвоїстою — можна поміняти місцями точки і прямі, зберігаючи при цьому всі властивості інцидентності конфігурації. Ця двоїстість надає графу Татта — Коксетера додаткових симетрій, що не належать симетріям конфігурації Кремони — Річмонда, які міняють місцями обидві частки двочасткового графу. Ці симетрії відповідають зовнішнім автоморфізмам симетричної групи шести елементів.

Реалізація

Будь-які шість точок у загальному положенні в чотиривимірному просторі дають 15 точок, які визначаються перетином прямих, що проходять через дві точки, з гіперплощинами, визначеними іншими чотирма точками. Таким чином, двійки відповідають один до одного цим отриманим 15 точкам. Будь-які три двійки, які разом утворюють набір, задають пряму, що є перетином трьох гіперплощин, які містять дві з трьох трійок з набору, і ця пряма містить усі точки, відповідні трьом двійкам набору. Таким чином, двійки і набори абстрактної конфігурації один до одного відповідають, у сенсі належності точок прямим, цим 15 точкам і 15 прямим, отриманим із початкових шести точок. Цю ж побудову можна спроєктувати в евклідів простір (3-вимірний) або на евклідову площину.[1]

Конфігурація Кремони — Річмонда має також сімейство реалізацій на площині, залежне від одного параметра, яке має циклічну симетрію п'ятого порядку.[2]

Історія

Шлефлі (Schläfli, 1858)(Schläfli, 1863) знайшов кубічні поверхні, що містять 15 дійсних прямих (додаткових до подвійної шістки Шлефлі у множині 27 прямих кубик) і 15 дотичних площин, по три прямих на кожній площині і по три площини, що проходять через кожну пряму. Перетин цих прямих і площин зі ще однією площиною дає конфігурацію 15₃15₃. Цю модель інциденцій прямих і площин Шлефлі пізніше опублікував Кремона (Cremona, 1868). Те, що отримана конфігурація не містить трикутників, помітив Мартінетті (Martinetti, 1886). Та сама конфігурація з'явилася в роботі Річмонда (Richmond, 1900). Вісконті (Visconti, 1916) виявив, що конфігурацію можна подати у вигляді самовписаного багатокутника. Бейкер використовував чотиривимірну реалізацію конфігурації як малюнок на обкладинці його двотомної роботи 1922—1925 Principles of Geometry (Основи геометрії). Захаріс (Zacharias, 1951) перевідкрив ту саму конфігурацію і виявив її реалізацію з циклічною симетрією п'ятого порядку.[3]

Назва конфігурації походить від робіт Кремони (Cremona, 1868)(Cremona, 1877) і Річмонда (Richmond, 1900). Можливо, внаслідок деяких помилок у роботах Мартінетті, його внесок залишився непоміченим.[3]

Примітка

Coxeter, 1950; Coxeter, 1958. Терміни двійки (duads) і набори (synthemes) взято зі статті Сильвестера (Sylvester, 1844), але Сильвестер використав ці системи пар і розкладів у контексті загальніших досліджень комплектів і розкладів множин, не надаючи особливої уваги множині зі шести елементів і не пов'язуючи цих множин із геометрією.
Zacharias, 1951; Boben, Pisanski, 2003; Boben, Grünbaum, Pisanski, Žitnik, 2006.
Історію конфігурації Кремони — Річмонда та більшість посилань взято зі статті Boben, Grünbaum, Pisanski, Žitnik, 2006. Посилання на Бейкера взято зі статті Коксетера (Coxeter, 1950).

Література

M. Boben, T. Pisanski. Polycyclic configurations // European Journal of Combinatorics. — 2003. — Т. 24, вип. 4 (17 лютого). — С. 431–457. — DOI:10.1016/S0195-6698(03)00031-3.
Marko Boben, Branko Grünbaum, Tomaž Pisanski, Arjana Žitnik. Small triangle-free configurations of points and lines // Discrete and Computational Geometry. — 2006. — Т. 35, вип. 3 (17 лютого). — С. 405–427. — DOI:10.1007/s00454-005-1224-9..
H. S. M. Coxeter. Self-dual configurations and regular graphs // Bulletin of the American Mathematical Society. — 1950. — Т. 56 (17 лютого). — С. 413–455. — DOI:10.1090/S0002-9904-1950-09407-5..
H. S. M. Coxeter. Twelve points in PG(5,3) with 95040 self-transformations // Proceedings of the Royal Society A. — 1958. — Т. 247, вип. 1250 (17 лютого). — С. 279–293. — DOI:10.1098/rspa.1958.0184..
L. Cremona. Mémoire de géométrie pure sur les surfaces du troisieme ordre // J. Reine Angew. Math.. — 1868. — Т. 68 (17 лютого). — С. 1–133.. Як процитовано в Boben, Grünbaum, Pisanski, Žitnik, 2006.
L. Cremona. Teoremi stereometrici dal quali si deducono le proprietà dell' esagrammo di Pascal. — 1877. — Т. 1 (17 лютого).
Branko Grünbaum. Configurations of points and lines. — Providence, R.I. : American Mathematical Society, 2009. — Т. 103. — (Graduate Studies in Mathematics) — ISBN 978-0-8218-4308-6.
V. Martinetti. Sopra alcune conﬁgurazioni piane // Annali di matematica pura ed applicata. — 1886. — Т. 14, вип. 1 (17 лютого). — С. 161–192. — DOI:10.1007/BF02420733..
H. W. Richmond. On the figure of six points in space of four dimensions. // Quart. J.. — 1900. — Т. 31 (17 лютого). — С. 125–160.
L. Schläfli. An attempt to determine the twenty-seven lines upon a surface of the third order, and to divide such surfaces into species in reference to the reality of the lines upon the surface // Quart. J. Pure Appl. Math.. — 1858. — Т. 2 (17 лютого). — С. 55–65, 110–120..
L. Schläfli. On the distribution of surfaces of the third order into species, in reference to the absence or presence of singular points, and the reality of their lines // Philosophical Transactions of the Royal Society. — 1863. — Т. 153 (17 лютого). — С. 193–241. — DOI:10.1098/rstl.1863.0010..
J. J. Sylvester. Elementary researches in the analysis of combinatorial aggregation // The Philos. Mag.. — 1844. — Т. 24 (17 лютого). — С. 285–295..
E. Visconti. Sulle conﬁgurazioni piane atrigone // Giornale di Matematiche di Battaglini. — 1916. — Т. 54 (17 лютого). — С. 27–41. Як процитовано в Boben, Grünbaum, Pisanski, Žitnik, 2006.
Max Zacharias. Streifzüge im Reich der Konfigurationen: Eine Reyesche Konfiguration (15₃), Stern- und Kettenkonfigurationen // Mathematische Nachrichten. — 1951. — Т. 5 (17 лютого). — С. 329–345. — DOI:10.1002/mana.19510050602..

Посилання

Weisstein, Eric W. Cremona–Richmond Configuration(англ.) на сайті Wolfram MathWorld.
Image ofCremona-Richmond configuration
Image ofCremona-Richmond configuration

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[cc-1] Coxeter, 1950; Coxeter, 1958. Терміни двійки (duads) і набори (synthemes) взято зі статті Сильвестера (Sylvester, 1844), але Сильвестер використав ці системи пар і розкладів у контексті загальніших досліджень комплектів і розкладів множин, не надаючи особливої уваги множині зі шести елементів і не пов'язуючи цих множин із геометрією.

[2] Zacharias, 1951; Boben, Pisanski, 2003; Boben, Grünbaum, Pisanski, Žitnik, 2006.

[bgpz-3] Історію конфігурації Кремони — Річмонда та більшість посилань взято зі статті Boben, Grünbaum, Pisanski, Žitnik, 2006. Посилання на Бейкера взято зі статті Коксетера (Coxeter, 1950).