Двоїстість (проєктивна геометрія)

Якщо визначати проєктивну площину аксіоматично як структуру інцидентності в термінах множини точок ${\displaystyle P}$, множини прямих ${\displaystyle L}$ і бінарного відношення інцидентності ${\displaystyle I}$, яке визначає, які точки лежать на яких прямих, то можна визначити двоїсту структуру площини.

Якщо обміняти ролями «точки» і «прямі» в структурі інцидентності

${\displaystyle C=(P,L,I)}$,

отримаємо двоїсту структуру

${\displaystyle C=(P,L,I)}$,

де ${\displaystyle I*}$ — обернене відношення до ${\displaystyle I}$. ${\displaystyle C*}$ є також проєктивною площиною, яка називається двоїстою (дуальною) площиною для ${\displaystyle C}$.

Якщо ${\displaystyle C}$ і ${\displaystyle C*}$ ізоморфні, то ${\displaystyle C}$ називається самодвоїстою. Проєктивні площини ${\displaystyle PG(2,K)}$ для будь-якого поля (або, в загальнішому випадку, для будь-якого кільця з поділом, ізоморфного двоїстого йому) ${\displaystyle K}$ є самодвоїстими. Зокрема, дезаргові площини скінченного порядку завжди самодвоїсті. Однак серед недезаргових площин існують як самодвоїсті (наприклад, площини Г'юза), так і не самодвоїсті (наприклад, площини Голла).

Для проєктивної площини твердження, що стосується точок, площин та їх інцидентності, отримане з іншого такого твердження шляхом обміну термінів «точка» і «пряма» (зі зміною, якщо потрібно, граматики), називається двоїстим твердженням. Двоїстим твердженням для «Через дві точки проходить єдина пряма» буде «Дві прямі перетинаються в одній точці». Утворення двоїстого твердження називається дуалізацією твердження.

Якщо твердження істинне в проєктивній площині ${\displaystyle C}$, то двоїсте твердження має бути істинним у двоїстій площині ${\displaystyle C*}$. Це випливає з того, що дуалізація кожного твердження в доведенні «в ${\displaystyle C}$» дає твердження в доведенні «в ${\displaystyle C}$».

Принцип двоїстості площини каже, що дуалізація будь-якої теореми в самодвоїстій проєктивній площині ${\displaystyle C}$ породжує іншу істинну теорему в ${\displaystyle C}$.

Цю концепцію можна узагальнити до двоїстості тривимірного простору, де поняття «точки» і «площини» міняються ролями (а прямі залишаються прямими).[1] Це приводить до принципу двоїстості простору. Можливі й подальші узагальнення (див. нижче).

Ці принципи дають хороший привід для вживання «симетричного» терміна для відношення інцидентності. Так, замість речення «точка лежить на прямій» можна сказати «точка і пряма інцидентні», і для дуалізації твердження достатньо слова точка і пряма переставити місцями («пряма і точка інцідентні»).

За визначенням, проєктивна площина являє собою множину точок і прямих, і проєктивне перетворення може відображати точки на точки і прямі на прямі. Таке перетворення називається колінеацією.[2] При розгляді двоїстості проєктивної площини розглядається інше відображення, за якого точки переходять у прямі, а прямі — в точки. Таке відображення називається кореляцією.[3] Проєктивне відображення визначається вимогами збереження:

1) інцидентності точок і прямих,

2) подвійного відношення[4].

Друга вимога використовує гармонійні четвірки точок на прямій, що утворюють проєктивний ряд точок, концепцію, двоїсту пучку прямих у точці.

Двоїстість (площини) — це відображення з проєктивної площини ${\displaystyle C=(P,L,I)}$ в її дуальну ${\displaystyle C^{*}=(L,P,I^{*})}$, що зберігає властивість інцидентності. Отже, двоїстість (площини) ${\displaystyle \sigma }$ відображає точки в прямі і прямі в точки (${\displaystyle P^{\sigma }=L}$ і ${\displaystyle L^{\sigma }=P}$) так, що, якщо точка ${\displaystyle Q}$ лежить на прямій ${\displaystyle m}$ (позначається ${\displaystyle QIm}$), то ${\displaystyle Q^{\sigma }I^{*}m^{\sigma }\Leftrightarrow m^{\sigma }I^{*}Q^{\sigma }}$. Двоїстість (площини), яка є ізоморфізмом, називається кореляцією.[5] Існування кореляції означає самодвоїстість проєктивної площини.

В особливому випадку, коли проєктивна площина має тип ${\displaystyle PG(2,K)}$, де ${\displaystyle K}$ — кільце з поділом, двоїстість називають взаємним перетворенням.[6] За основною теоремою проєктивної геометрії взаємне перетворення є композицією автоморфної функції на ${\displaystyle K}$ і про'єктивного перетворення. Якщо використовуваний автоморфізм є тотожним, то взаємне перетворення називають проєктивною кореляцією.

Кореляцію другого порядку (інволюція) називають поляритетом. Якщо кореляція не є поляритетом, то ${\displaystyle \phi ^{2}}$ буде нетривіальною колінеацією.

Цю концепцію відображення можна поширити й на простори вищих розмірностей, так що згадку про площину можна вилучити.

Двоїстість проєктивної площини є окремим випадком двоїстості для проєктивних просторів, перетворень ${\displaystyle PG(n,K)}$ (які позначають також ${\displaystyle KP^{n}}$), де ${\displaystyle K}$ — поле, які обмінюють об'єкти розмірності ${\displaystyle r}$ з об'єктами розмірності ${\displaystyle n-1-r}$ (= корозмірність ${\displaystyle r+1}$). Отже, в проєктивному просторі розмірності ${\displaystyle n}$ точки (розмірність 0) відповідатимуть гіперплощинам (корозмірність 1), прямі, що проходять через дві точки (розмірність 1), відповідатимуть перетинам двох гіперплощин (корозмірність 2), і так далі.

Точки ${\displaystyle PG(n,K)}$ можна розглядати як ненульові вектори в ${\displaystyle (n+1)}$-вимірному векторному просторі над ${\displaystyle K}$, в якому ми ототожнюємо два вектори, якщо вони відрізняються лише множенням на скаляр. Інший спосіб подання як точки ${\displaystyle n}$-вимірного проєктивного простору — як прямі, що проходять через початок координат у ${\displaystyle K^{n+1}}$, які є 1-вимірними векторними підпросторами. Отже, ${\displaystyle n}$-вимірні векторні підпростори поля ${\displaystyle K^{n+1}}$ подають ${\displaystyle (n-1)}$-вимірні геометричні гіперплощини проєктивних ${\displaystyle n}$-просторів над ${\displaystyle K}$.

Ненульовий вектор u = (u₀,u₁,…,u_n) у ${\displaystyle K^{n+1}}$ визначає ${\displaystyle (n-1)}$-вимірний геометричний підпростір (гіперплощину) H_u,

H_u = (x₀,x₁,…,x_n) : u₀x₀ + … + u_nx_n = 0.

Вектор u, який використовується для визначення гіперплощини, позначимо u_H, а для позначення точки, відповідної кінцю вектора, використаємо позначення u_P. У термінах звичайного скалярного добутку, H_u = {x_P : u_H • x_P = 0}. Оскільки K є полем, скалярний добуток симетричний, що означає u_H•x_P = u₀x₀ + u₁x₁ + … + u_nx_n = x₀u₀ + x₁u₁ + … + x_nu_n = x_H•u_P. Можна задати взаємне перетворення u_P ↔ H_u між точками і гіперплощинами. Цю відповідність можна поширити на прямі, утворені двома точками і перетин двох гіперплощин, і т. далі.

На проективній площині ${\displaystyle PG(2,K)}$ з полем ${\displaystyle K}$ ми маємо відповідність: однорідні координати (a, b,c) ↔ прямі, що задаються рівняннями ax + by + cz = 0. У проєктивному просторі ${\displaystyle PG(3,K)}$ є відповідність: точки в однорідних координатах (a, b,c, d) ↔ площині, що задаються рівняннями ax + by + cz + dw = 0. Ця відповідність також відображає пряму, задану двома точками (a_1,b_1,c_1,d₁) і (a₂,b₂,c₂,d₂), в пряму, яка є перетином двох площин, заданих рівняннями a₁x + b₁y + c₁z + d₁w = 0 и a₂x + b₂y + c₂z + d₂w = 0.

У полярних відображеннях дійсного проєктивного 3-вимірного простору ${\displaystyle PG(3,R)}$ точки відповідають площинам, а прямі — прямим. У стереометрії має місце двоїстість многогранників, коли точки двоїсті граням, а ребра двоїсті ребрам, так що ікосаедр двоїстий додекаедру, а куб двоїстий октаедру.

Відповідність у ${\displaystyle PG(2,R)}$ в однорідних координатах можна описати геометрично. Для цього використовується модель дійсної проєктивної площини «одинична сфера з ототожненням антиподів[7]», або, що еквівалентно, модель прямих і площин, які проходять через початок координат простору R³. Зіставимо прямій, що проходить через початок координат, унікальну площину, що проходить через початок координат і перпендикулярна (ортогональна) до прямої. Якщо в цій моделі прямі вважати точками, а площини — прямими проєктивної площини ${\displaystyle PG(2,R)}$, це зіставлення стає відповідністю (а фактично — полярним відображенням) проєктивної площини. Сферичну модель можна отримати як перетин прямих і площин, що проходять через початок координат, з одиничною сферою, що має центр у початку координат. Прямі перетинають сферу в двох протилежних точках, які ототожнюються для отримання точки проективної площини, площини ж перетинають сферу по великих колах, які є прямими проєктивної площини.

Те, що таке зіставлення «зберігає» інцидентність, легко показати на моделі прямих і площин. Точка, інцидентна прямій у проєктивній площині, відповідає прямій, що лежить на площині в моделі. Згідно із зіставленням, площина стає прямою, що проходить через початок координат і перпендикулярна до площини, якій зіставлена. Цей образ (пряма) перпендикулярна до будь-якої прямої, що лежить на площині, зокрема й до початкової прямої (точки проєктивної площини). Всі прямі, що проходять через початок координат і перпендикулярні до початкової прямої, лежать в одній площині, перпендикулярній до початкової прямої, яка зіставлена початковій прямій. Отже, образ прямої лежить в образі площині, так що інцидентність збережено.

Полюс і поляра відносно кола O. P = Q', q — поляра для Q, Q — полюс для q.

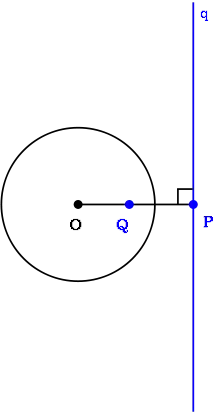
В евклідовому просторі виберемо коло C з центром O і радіусом r. Для кожної точки P, відмінної від O, визначимо образ Q', так що OP • OQ = r². Відображення P → Q називається інверсією[8] відносно кола C. Пряма q, що проходить через P, перпендикулярна OP, називається полярою точки Q відносно кола C.

Нехай q — пряма, що не проходить через O. Опустимо перпендикуляр з O на q, який перетинає q в точці P (це найближча до O точка прямої q). Образ точки Q (точка P) при інверсії відносно C називається полюсом прямої q. Якщо точка M лежить на прямій q (що не проходить через O), то полюс прямої q лежить на полярі точки M і навпаки. Процес, що зберігає інцидентність, за якого точки і прямі переходять в їхні поляри і полюси, відносно C називається проєктивним перетворенням.[9]

Щоб зробити цей процес взаємним перетворенням, евклідів простір (який не є проективною площиною) слід розширити до розширеної евклідової площині доданням прямої на нескінченності і точок на нескінченності, які лежать на цій нескінченно віддаленій прямій. На цій розширеній площині ми визначаємо поляру точки O як пряму на нескінченності (і O є полюсом на нескінченності), і полюси прямих, що проходять через O як точки на нескінченності, де, якщо пряма має кутовий коефіцієнт s (≠ 0), її полюс є нескінченно віддаленою точкою, що відповідає класу паралельних прямих з нахилом -1/s. Полюс для осі x — це точка на нескінченності вертикальних прямих, а полюс осі y — точка на нескінченності горизонтальних прямих.

Побудову полярного перетворення для інверсії відносно кола, наведену вище, можна узагальнити з використанням інверсії відносно конічних перетинів (на розширеній дійсній площині). Взаємне перетворення, побудоване таким чином, є проєктивною кореляцією другого порядку, тобто полярним перетворенням.

Модель проєктивної площини з одиничною сферою ізоморфна (беручи до уваги властивість інцидентності) планарної моделі, де площину розширено проєктивною прямою на нескінченності. У цій моделі протилежні точки сфери (відносно центру) вважаються однією точкою.

Щоб зіставити точкам сфери точки на площині, припустимо, що сфера дотикається до площини в певній точці і цю точку ми виберемо як початок координат площини. Тепер проведемо пряму через точку на сфері і центр сфери. Ця пряма перетне сферу в деякій точці. Отриману точку можна використати для побудови взаємно однозначного відображення

${\displaystyle f:[0,\pi /2]\times [0,2\pi ]\rightarrow \mathbb {R} P^{2}.}$

Якщо точки в ${\displaystyle \mathbb {R} P^{2}}$ задано в однорідних координатах, то

${\displaystyle f:(\theta ,\phi )\mapsto [\cos \phi$ :\sin \phi :\cot \theta ],}

${\displaystyle f^{-1}:[x:y:z]\mapsto \left(\arctan {\sqrt {\left({x \over z}\right)^{2}+\left({y \over z}\right)^{2}}},\arctan _{2}(y,x)\right).}$

Прямі на планарній моделі є проєкціями великих кіл сфери, оскільки через пряму на площині і початок 3-вимірних координат можна провести площину, і ця площина буде перетинати сферу по великому колу.

Як можна бачити, будь-якому великому колу на сфері можна зіставити проєктивну точку, відповідну єдиній прямій, перпендикулярній до площини, на якій лежить коло і яку можна визначити як двоїсту. Ця пряма перетинає дотичну площину, і це показує, як зіставити єдину точку площини будь-якій прямій цієї площини, так, що точка буде двоїстою до прямої.

• A. Adrian Albert, Reuben Sandler. An Introduction to Finite Projective Planes. — New York : Holt, Rinehart and Winston, 1968. — 3 листопада.
• F. Bachmann, 1959. Aufbau der Geometrie aus dem Spiegelungsbegriff, Springer, Berlin.
• Р. Бэр. Линейная алгебра и проективная геометрия. — Москва : Издательство иностранной литературы, 1955.
• M.K. Bennett. Affine and Projective Geometry. — New York : Wiley, 1995. — ISBN 0-471-11315-8.
• Albrecht Beutelspacher, Ute Rosenbaum. Projective Geometry: from foundations to applications. — Cambridge : Cambridge University Press, 1998. — ISBN 0-521-48277-1.
• Rey Casse. Projective Geometry: An Introduction. — New York : Oxford University Press, 2006. — 3 листопада. — ISBN 0-19-929886-6.
• Judith N. Cederberg. A Course in Modern Geometries. — New York : Springer-Verlag, 2001. — ISBN 0-387-98972-2.
• Г.С.М. Коксетер. Действительная проективная плоскость. — Москва : Государственное издательство физико-математической литературы, 1959.
• Coxeter, H. S. M. Projective Geometry. — 2nd ed. — Springer Verlag, 2003. — ISBN 978-0-387-40623-7.
• Г.С.М. Коксетер. Введение в геометрию. — Москва : «Наука» Главная редакция физико-математической литературы, 1968.
• Г.С.М. Коксетер, С.Л. Грейтцер. Новые встречи с геометрией. — Москва : «Наука» Главная редакция физико-математической литературы, 1978. — (Библиотека математического кружка)
• Dembowski Peter. Finite Geometries. — Berlin : Springer Verlag, 1968.
• Lynn E. Garner. An Outline of Projective Geometry. — New York : North Holland, 1981. — ISBN 0-444-00423-8.
• Greenberg, M.J. Euclidean and non-Euclidean geometries. — 4th ed. — Freeman, 2007.
• Р. Хартсхорн. Основы проективной геометрии. — Москва : «Мир», 1970. — («Современная математика» Популярная серия)
• Hartshorne Robin. Geometry: Euclid and Beyond. — Springer, 2000.
• Д. Гилберт, С. Кон-Фоссен. Наглядная геометрия. — Москва, Ленинград : Главная редакция общетехнической литературы и номографии, 1936.
• D. R. Hughes, F. C. Piper. Projective Planes. — Springer, 1973.
• F. Kárteszi. Introduction to Finite Geometries. — Amsterdam : North-Holland, 1976. — ISBN 0-7204-2832-7.
• R.J. Mihalek. Projective Geometry and Algebraic Structures. — New York : Academic Press, 1972. — ISBN 0-12-495550-9.
• S. Ramanan. Projective geometry // Resonance. — Springer India, 1997. — Т. 2, вип. 8 (1 серпня). — С. 87–94. — ISSN 0971-8044. — DOI:10.1007/BF02835009.
• Pierre Samuel. Projective Geometry. — New York : Springer-Verlag, 1988. — ISBN 0-387-96752-4.
• Frederick W. Stevenson. Projective Planes. — San Francisco : W.H. Freeman and Company, 1972. — 3 листопада. — ISBN 0-7167-0443-9.
• Oswald Veblen, J. W. A. Young. Projective geometry. — Boston : Ginn & Co, 1938. — ISBN 978-1-4181-8285-4.
• О.А. Вольберг. Основные идеи проективной геометрии. — Москва, Ленинград : Учпедгиз, 1949.
• С.Л. Певзнер. Проективная геометрия. — М. : «Просвещение», 1980. — С. 68—69 § 13 Коллинеации.

Weisstein, Eric W. Принцип двоїстості(англ.) на сайті Wolfram MathWorld.