Куб Фібоначчі

Куби Фібоначчі (намальовані червоним кольором) як підграфи гіперкубів

Куб Фібоначчі порядку 6

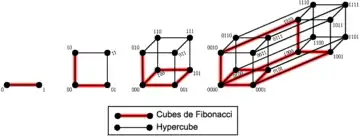
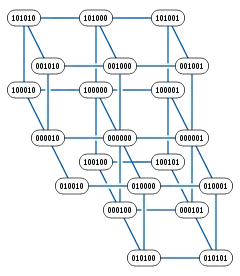
Подібно до графу гіперкуба, вершини куба Фібоначчі порядку n можна позначити бітовими рядками довжини n таким чином, що дві вершини суміжні, якщо їхні мітки відрізняються одним бітом. Однак в кубі Фібоначчі дозволені тільки мітки, які (як бітові рядки) не мають двох одиниць поспіль. Є ${\displaystyle F_{n+2}}$ можливих міток, де ${\displaystyle F_{n}}$ позначає ${\displaystyle n}$-е число Фібоначчі, а тому є ${\displaystyle F_{n+2}}$ вершин в кубі Фібоначчі порядку n.

Вузлам таких мереж можуть бути призначені послідовні цілі числа від ${\displaystyle 0}$ до ${\displaystyle F_{n+2}-1}$ . Бітові рядки, які відповідають цим числам, задаються їх поданнями Цекендорфа[2].

Куб Фібоначчі порядку ${\displaystyle n}$ є симплектичним графом доповнення графу шляху з ${\displaystyle n}$ вершинами[3]. Тобто, кожна вершина куба Фібоначчі представляє кліку в доповненні шляху або, що еквівалентно, в незалежній множині в самому шляху. Дві вершини куба Фібоначчі суміжні, якщо кліки або незалежні множини, які вони представляють, відрізняються видаленням або додаванням одного елемента. Тому, подібно до інших симплексних графів, куби Фібоначчі є медіанними графами і, більш загально, частковими кубами[4][5]. Медіана будь-яких трьох вершин куба Фібоначчі може бути знайдена шляхом обчислення побітової мажоритарної функції трьох міток. Якщо кожна із трьох міток не має двох послідовних бітів 1, то це виконується і для їх мажоритарного значення.

Куб Фібоначчі є також графом дистрибутивної ґратки, яка може бути отримана через теорему Біркгофа з «паркану», частково впорядкованої множини, визначеної почерговою послідовністю відношень ${\displaystyle a<b>c<d>e<f>\dots }$[6]. Є також альтернативний опис мовою теорії графів тієї ж ґратки: незалежні множини будь-якого двочасткового графу можуть бути дані в певному порядку, в якому одна незалежна множина менша від іншої, якщо вони отримані шляхом видалення елементів з однієї частини і додавання елементів в іншу частину. З цим порядком незалежні множини утворюють дистрибутивну ґратку[7], а застосування даної побудови до графу-шляху призводить до асоціації решітки з кубом Фібоначчі.

Куб Фібоначчі порядку ${\displaystyle n}$ можна розбити на куб Фібоначчі порядку ${\displaystyle n-1}$ (розмітка вузлів починається з біта, що має значення 0) і куб Фібоначчі порядку ${\displaystyle n-2}$ (вузли починаються з біта значенням 1)[8].

Будь-який куб Фібоначчі має гамільтонів шлях. Конкретніше, існує шлях, який обходить розбиття, описане вище — він відвідує вузли спочатку з 0, а потім з 1 у двох неперервних підпослідовностях. У цих двох підпослідовностях шлях може бути побудований рекурсивно за тим самим правилом, з'єднуючи дві підпослідовності кінцями, на яких другий біт має значення 0. Тоді, наприклад, у кубі Фібоначчі порядку 4 послідовністю, побудованою таким чином, буде (0100-0101-0001- 0000-0010) — (1010-1000-1001), де дужки показують підпослідовності двох підграфів. Куби Фібоначчі з парним числом вузлів, більшим від двох, мають гамільтонів цикл[9].

Мунаріні і Сальві[10] вивчали радіус і число незалежності кубів Фібоначчі. Оскільки ці графи двочастинні і мають гамільтонів шлях, їхні максимальні незалежні множини мають число вершин, що дорівнює половині вершин усього графу, округлене до найближчого цілого[11]. Діаметр куба Фібоначчі порядку n дорівнює n, а його радіус дорівнює n/2 (знову, округлений до найближчого цілого)[12].

Тараненко і Весель[13] показали, що можна перевірити, чи є граф кубом Фібоначчі за час, близький до його розміру.

Сюй[1], а також Сюй, Пейдж і Лью[14] запропонували використовувати куби Фібоначчі як мережеву топологію в системах паралельних обчислень. Як комунікаційна мережа куб Фібоначчі має корисні властивості, подібні до властивостей гіперкуба — число інцидентних ребер на одну вершину не більше ніж ${\displaystyle n/2}$, і діаметр мережі не перевищує ${\displaystyle n}$, обидва значення пропорційні логарифму числа вершин, а можливість розбити мережу на менші підмережі того ж типу дозволяє розщепити багато завдань паралельних обчислень[9]. Куби Фібоначчі підтримують також ефективні протоколи для маршрутизації і широкомовлення в системах розподілених обчислень[1][15].

Клавжар і Жігерт застосували куби Фібоначчі в хімічній теорії графів як опис сімейства досконалих парувань деяких молекулярних графів[16]. Для молекулярної структури, описуваної планарним графом ${\displaystyle G}$, резонансним графом (або графом ${\displaystyle Z}$-перетворення) графу ${\displaystyle G}$ є граф, вершини якого описують досконалі парування графу ${\displaystyle G}$, а ребра якого з'єднують пари досконалих парувань, симетрична різниця яких є внутрішньою гранню графу ${\displaystyle G}$. Поліциклічні ароматичні вуглеводні можуть бути описані як підграфи шестикутної мозаїки площини, а резонансні графи описують можливі структури з подвійними зв'язками цих молекул. Як показали Клавжар і Жігерт[16], вуглеводні, утворені ланцюжками шестикутників, сполучених ребро до ребра без трьох суміжних шестикутників на прямій, мають резонансні графи, які точно є графами Фібоначчі. Більш загально, Чжан, Оу і Яо описали клас планарних двочастинних графів, які мають куби Фібоначчі як графи резонансу[17][3].

Узагальнені куби Фібоначчі запропонували Сюй і Чжан[18], базуючись на числах Фібоначчі ${\displaystyle k}$-го порядку, які пізніше Сюй, Чжан і Дас, ґрунтуючись на більш загальних видах лінійних рекурсій, розширили на клас мереж, названих лінійними рекурсивними мережами[19]. Ву модифікував куби Фібоначчі другого порядку, ґрунтуючись на інших початкових умовах[20]. Інший пов'язаний граф — куб Люка, з кількістю вершин, рівним числу Люка, визначений з куба Фібоначчі шляхом заборони біта зі значенням 1 як у першій, так і в останній позиції кожного бітового рядка. Дідо, Торрі і Салві використовували властивості розмальовки як кубів Фібоначчі, так і кубів Люка[21].

• István Beck. Partial orders and the Fibonacci numbers // Fibonacci Quarterly. — 1990. — Т. 28, вип. 2. — С. 172–174.
• Cong B., Zheng S. Q., Sharma S. On simulations of linear arrays, rings and 2D meshes on Fibonacci cube networks // Proc. 7th Int. Parallel Processing Symposium. — 1993. — С. 748–751. — DOI:10.1109/IPPS.1993.262788.
• Ernesto Dedó, Damiano Torri, Norma Zagaglia Salvi. The observability of the Fibonacci and the Lucas cubes // Discrete Mathematics. — 2002. — Т. 255, вип. 1–3. — С. 55–63. — DOI:10.1016/S0012-365X(01)00387-9.
• Emden R. Gansner. On the lattice of order ideals of an up-down poset // Discrete Mathematics. — 1982. — Т. 39, вип. 2. — С. 113–122. — DOI:10.1016/0012-365X(82)90134-0.
• Hartmut Höft, Margret Höft. A Fibonacci sequence of distributive lattices // Fibonacci Quarterly. — 1985. — Т. 23, вип. 3. — С. 232–237.
• Hsu W.-J. Fibonacci cubes: a new interconnection topology // IEEE Transactions on Parallel and Distributed Systems. — 1993. — Т. 4, вип. 1. — С. 3–12. — DOI:10.1109/71.205649.
• Hsu W.-J., Chung M. J. Generalized Fibonacci cubes // 1993 International Conference on Parallel Processing - ICPP'93. — 1993. — Т. 1. — С. 299–302. — DOI:10.1109/ICPP.1993.95.
• Hsu W.-J., Page C. V., Liu J.-S. Fibonacci cubes: a class of self-similar graphs // Fibonacci Quarterly. — 1993. — Т. 31, вип. 1. — С. 65–72.
• Hsu W.-J., Chung M. J., Das A. Linear recursive networks and their applications in distributed systems // IEEE Transactions on Parallel and Distributed Systems. — 1997. — Т. 8, вип. 7. — С. 673–680. — DOI:10.1109/71.598343.
• Sandi Klavžar. On median nature and enumerative properties of Fibonacci-like cubes // Discrete Mathematics. — 2005. — Т. 299, вип. 1–3. — С. 145–153. — DOI:10.1016/j.disc.2004.02.023.
• Sandi Klavžar. Structure of Fibonacci cubes: a survey // IMFM Preprint Series. — Ljubljana, Slovenia : Institute of Mathematics, Physics and Mechanics, 2011. — Т. 49, вип. 1150.
• Sandi Klavžar, Petra Žigert. Fibonacci cubes are the resonance graphs of Fibonaccenes // Fibonacci Quarterly. — 2005. — Т. 43, вип. 3. — С. 269–276..
• Emanuele Munarini, Norma Zagaglia Salvi. Structural and enumerative properties of the Fibonacci cubes // Discrete Mathematics. — 2002. — Т. 255, вип. 1–3. — С. 317–324. — DOI:10.1016/S0012-365X(01)00407-1.
• James Propp. Generating random elements of finite distributive lattices // Electronic Journal of Combinatorics. — 1997. — Т. 4, вип. 2. — С. R15. — arXiv:math.CO/9801066.
• Rodolfo Salvi, Norma Zagaglia Salvi. Alternating unimodal sequences of Whitney numbers // Ars Combinatoria. — 2008. — Т. 87. — С. 105–117.
• Richard P. Stanley. Enumerative Combinatorics. — Wadsworth, Inc., 1986. Упражнение 3.23a, страница 157
• Ivan Stojmenovic. Optimal deadlock-free routing and broadcasting on Fibonacci cube networks // Utilitas Mathematica. — 1998. — Т. 53. — С. 159–166..
• Taranenko A., Vesel A. Fast recognition of Fibonacci cubes // Algorithmica. — 2007. — Т. 49, вип. 2. — С. 81–93. — DOI:10.1007/s00453-007-9026-5.
• Jie Wu. Extended Fibonacci cubes // IEEE Transactions on Parallel and Distributed Systems. — 1997. — Т. 8, вип. 12. — С. 1203–1210. — DOI:10.1109/71.640012.
• Heping Zhang, Lifeng Ou, Haiyuan Yao. Fibonacci-like cubes as Z-transformation graphs // Discrete Mathematics. — 2009. — Т. 309, вип. 6. — С. 1284–1293. — DOI:10.1016/j.disc.2008.01.053.