Частковий куб

В. Фірсов[2] першим досліджував ізометричні вкладення графів у гіперкуби. Графи, що дозволяють такі вкладення, описані Д. Джоковичем[3] і П. Вінклером[4], пізніше отримали назву «часткові куби». Окремо ці ж структури в термінології сімейств множин, а не розмітки гіперкубів, досліджували, серед інших, В. Кузьмін і С. Овчинніков[5], а також Фалмагне і Дойнон[6][7].

Приклад часткового куба з розміткою Геммінга у вершинах. Граф є також медіанним графом.

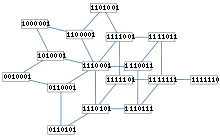
Будь-яке дерево є частковим кубом. Припустимо, що дерево T має m ребер і номери цих ребер (в довільному порядку) від 0 до m − 1. Виберемо довільну кореневу вершину r для дерева, і надамо кожній вершині v позначку (бітовий рядок) довжиною m біт, у якій стоїть 1 у позиції i, якщо ребро i лежить на шляху з r до v в дереві T. Наприклад, сама вершина r матиме позначку з нулів, а всі сусідні їй вершини будуть мати 1 в одній позиції, і т. д. Тоді відстань Геммінга між будь-якими двома позначками дорівнюватиме відстані між відповідними вершинами дерева, так що така розмітка показує, що дерево T є частковим кубом.

Будь-який граф гіперкуба є сам частковим кубом, який можна розмітити різними бітовими рядками з довжиною, що дорівнює розмірності гіперкуба.

Складніші приклади:

• Розглянемо граф, вершини якого складаються з усіх можливих бітових рядків довжиною 2n + 1, які мають або n, або n + 1 ненульових біт. Дві вершини цього графу суміжні, якщо їх мітки відрізняються на єдиний біт. Така розмітка визначає вкладення цього графу в гіперкуб (граф усіх бітових рядків заданої довжини з тією ж умовою суміжності). Отриманий граф є двочастинним кнезеровим графом. Граф, отриманий таким способом з n = 2, має 20 вершин і 30 ребер і називається графом Дезарга.
• Всі медіанні графи є частковими кубами[8]. Дерева і гіперкуби є окремими випадками медіанних графів. Оскільки до медіанних графів належать рамкові графи, симплекс-графи і куби Фібоначчі, а також покривні графи скінченних дистрибутивних ґраток, всі вони є частковими кубами.
• Графи, двоїсті конфігураціям прямих на евклідовій площині, є частковими кубами. У загальнішому вигляді, для будь-якої конфігурації гіперплощин у евклідовому просторі будь-якої розмірності граф, що має вершину для кожної комірки конфігурації і ребро для будь-яких двох суміжних комірок, є частковим кубом[9].
• Частковий куб, у якому кожна вершина має рівно три сусіди, відомий як кубічний частковий куб. Хоча деякі нескінченні сімейства кубічних часткових кубів відомі, разом з іншими спорадичними прикладами, єдиний відомий кубічний частковий куб, який не є планарним, — це граф Дезарга[10].
• Граф, що лежить в основі будь-якого антиматроїда, що має вершину для кожної множини в антиматроїді і ребро для будь-яких двох множин, що відрізняються єдиним елементом, завжди є частковим кубом.
• Прямий добуток будь-якої скінченної множини часткових кубів є іншим частковим кубом[11].

Багато теорем про часткові куби спираються прямо або побічно на деяке бінарне відношення, визначене на ребрах графу. Це відношення, вперше описане Джоковичем[3], позначається ${\displaystyle \Theta }$. Вінклер дав еквівалентне визначення співвідношення в термінах відстані[4]. Два ребра ${\displaystyle e=\{x,y\}}$ і ${\displaystyle f=\{u,v\}}$ перебувають у відношенні ${\displaystyle \Theta }$ (записується ${\displaystyle e{\mathrel {\Theta }}f}$), якщо ${\displaystyle d(x,u)+d(y,v)\not =d(x,v)+d(y,u)}$. Це відношення є рефлексивним і симетричним, але, в загальному випадку, не транзитивним.

Вінклер показав, що зв'язний граф є частковим кубом тоді і тільки тоді, коли він є двочастковим і відношення ${\displaystyle \Theta }$ транзитивне[12][13]. У цьому випадку відношення утворює відношення еквівалентності і кожен клас еквівалентності відокремлює два зв'язних підграфи графу один від одного. Розмітку Геммінга можна отримати призначенням одного біта в кожній позначці для кожного класу еквівалентності співвідношення Джоковича — Вінклера. В одному з двох зв'язних підграфів, розділених співвідношенням еквівалентності ребер, позначки мають 0 у відповідній позиції, а в іншому зв'язному підграфі всі позначки в тій самій позиції мають 1.

Часткові куби можна розпізнати і побудувати для них розмітку Геммінга за час ${\displaystyle O(n^{2})}$, де ${\displaystyle n}$ — число вершин графу[14]. Якщо задано частковий куб, можна безпосередньо побудувати класи еквівалентності відношення Джоковича — Вінклера використовуючи пошук у ширину від кожної вершини за загальний час ${\displaystyle O(nm)}$. Алгоритм розпізнавання з часом роботи ${\displaystyle O(n^{2})}$ прискорює пошук, використовуючи для здійснення множинних пошуків у ширину за один прохід графу паралелізм бітового рівня, потім використовується окремий алгоритм для перевірки, що отримано правильну розмітку часткового куба.

Ізометрична розмірність часткового куба — це мінімальна розмірність гіперкуба, в який можна вкласти граф ізометрично і вона дорівнює числу класів еквівалентності відношення Джоковича — Вінклера. Наприклад, ізометрична розмірність дерева з ${\displaystyle n}$ вершинами дорівнює числу його ребер, ${\displaystyle n-1}$. Вкладення часткового куба в гіперкуб такої розмірності єдине з точністю до симетрій гіперкуба[15][16].

Будь-який гіперкуб, а тому і будь-який частковий куб, можна вкласти ізометрично в цілочисельну ґратку і розмірність ґратки для часткового куба — це мінімальна розмірність цілочисельної ґратки, в яку можна вкласти частковий куб. Розмірність ґратки може виявитися істотно меншою від ізометричної розмірності. Наприклад, для дерева вона дорівнює половині числа листків у дереві (з округленням до найближчого цілого). Розмірність ґратки для будь-якого графу і вкладення в ґратку мінімальної розмірності можна знайти за поліноміальний час алгоритмом, заснованим на пошуку найбільшого парування в допоміжному графі[17].

Визначаються й інші типи розмірностей часткового куба, засновані на специфічніших структурах[18][19].

Ізометричні вкладення графів у гіперкуб мають важливе застосування в хімічній теорії графів. Бензоїдний граф — це граф, що складається з вершин і ребер, які лежать на циклі і всередині циклу в шестикутній ґратці. Такі графи є молекулярними графами бензоїдних вуглеводнів, великого класу органічних молекул. Кожен такий граф є частковим кубом. Розмітку Геммінга такого графу можна використати для обчислення індексу Вінера відповідної молекули, який можна використовувати для передбачення деяких хімічних властивостей[20]. Інша молекулярна структура, утворена вуглецем, структура алмазу, також відповідає частковим кубам[18].

• S. Cabello, D. Eppstein, S. Klavžar. The Fibonacci dimension of a graph // Electronic Journal of Combinatorics. — 2011. — Т. 18, вип. 1 (17 лютого). — arXiv:0903.2507.
• D. Ž. Djoković. Distance-preserving subgraphs of hypercubes // Journal of Combinatorial Theory. — 1973. — Т. 14, вип. 3 (17 лютого). — С. 263–267. — DOI:10.1016/0095-8956(73)90010-5.
• David Eppstein. The lattice dimension of a graph // European Journal of Combinatorics. — 2005. — Т. 26, вип. 6 (17 лютого). — С. 585–592. — arXiv:cs.DS/0402028. — DOI:10.1016/j.ejc.2004.05.001.
• David Eppstein. Cubic partial cubes from simplicial arrangements // Electronic Journal of Combinatorics. — 2006. — Т. 13, вип. 1 (17 лютого). — arXiv:math.CO/0510263.
• David Eppstein. Proc. 19th ACM-SIAM Symposium on Discrete Algorithms. — 2008. — С. 1258–1266.
• David Eppstein. Proc. 16th International Symposium on Graph Drawing, Heraklion, Crete, 2008. — Springer-Verlag, 2009. — Т. 5417. — С. 384–389. — (Lecture Notes in Computer Science) — DOI:10.1007/978-3-642-00219-9_37.
• J.-C. Falmagne, J.-P. Doignon. Stochastic evolution of rationality // Theory and Decision. — 1997. — Т. 43 (17 лютого). — С. 107–138. — DOI:10.1023/A:1004981430688.
• Фирсов В. В. Об изометрическом вложении графа в булевский куб // Кибернетика. — 1965. — Вип. 6 (17 лютого). — С. 95-96.
• F. Hadlock, F. Hoffman. Manhattan trees // Utilitas Mathematica. — 1978. — Т. 13 (17 лютого). — С. 55–67. Як процитовано в (Ovchinnikov, 2011).
• Wilfried Imrich, Sandi Klavžar. Product Graphs: Structure and Recognition. — New York : John Wiley & Sons, 2000. — (Wiley-Interscience Series in Discrete Mathematics and Optimization) — ISBN 978-0-471-37039-0.
• Sandi Klavžar, Ivan Gutman, Bojan Mohar. Labeling of benzenoid systems which reflects the vertex-distance relations // Journal of Chemical Information and Computer Sciences. — 1995. — Т. 35, вип. 3 (17 лютого). — С. 590–593. — DOI:10.1021/ci00025a030.
• В. Б. Кузьмин, С. В. Овчинников. Геометрия пространств предпочтений. I // Автоматика и телемеханика. — 1975. — Вип. 12 (17 лютого). — С. 140-145.
• Sergei Ovchinnikov. Graphs and Cubes. — Springer, 2011. — (Universitext). См. главу 5, «Partial Cubes», стр. 127—181.
• Peter M. Winkler. Isometric embedding in products of complete graphs // Discrete Applied Mathematics. — 1984. — Т. 7, вип. 2 (17 лютого). — С. 221–225. — DOI:10.1016/0166-218X(84)90069-6.