Ланцюгова гомотопія

Нехай ${\displaystyle X}$ і ${\displaystyle Y}$ — ланцюгові комплекси модулів (тобто множина модулів ${\displaystyle X_{k},\;Y_{k}}$ і модульних гомоморфізмів ${\displaystyle d_{X}^{k}\colon X_{k}\to X_{k-1},\;d_{Y}^{k}\colon Y_{k}\to Y_{k-1}}$), ${\displaystyle f}$ і ${\displaystyle g}$ — ланцюгові відображення комплексу ${\displaystyle X}$ в комплекс ${\displaystyle Y}$ (тобто такі гомоморфізми ${\displaystyle f_{k}}$ що ${\displaystyle d_{Y}^{k}f_{k}=f_{k-1}d_{X}^{k}}$).

Ланцюговою гомотопією між відображеннями ${\displaystyle f}$ і ${\displaystyle g}$ називається множина гомоморфізмів ${\displaystyle D_{k}\colon X_{k}\to Y_{k+1}}$, для яких справедливими є рівності

${\displaystyle D_{k-1}d_{X}^{k}+d_{Y}^{k+1}D_{k}=f_{k}-g_{k}.}$

Аналогічно можна ввести поняття ланцюгової гомотопії для коланцюгових комплексів ${\displaystyle X}$ і ${\displaystyle Y.}$ Якщо ${\displaystyle f}$ і ${\displaystyle g}$ — коланцюгові відображення комплексу ${\displaystyle X}$ в комплекс ${\displaystyle Y}$ (тобто такі гомоморфізми ${\displaystyle f_{k}}$ що ${\displaystyle d_{Y}^{k}f_{k}=f_{k+1}d_{X}^{k}}$).

Ланцюговою гомотопією між відображеннями ${\displaystyle f}$ і ${\displaystyle g}$ називається множина гомоморфізмів ${\displaystyle D_{k}\colon X_{k}\to Y_{k-1}}$, для яких справедливими є рівності

${\displaystyle D_{k+1}d_{X}^{k}+d_{Y}^{k-1}D_{k}=f_{k}-g_{k}.}$

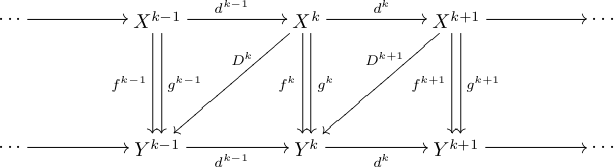
Діаграма для випадку коланцюгових комплексів зображена нижче:

• Відношення ланцюгової гомотопії є відношенням еквівалентності на множині ланцюгових відображень (і також на множині коланцюгових відображень). Дійсно відображення ${\displaystyle D_{k}=0}$ є ланцюговою гомотопією, що забезпечує рефлексивність. Якщо відображення ${\displaystyle D_{k}}$ є ланцюговою гомотопією між ланцюговими відображеннями ${\displaystyle f}$ і ${\displaystyle g}$, то ${\displaystyle -D_{k}}$ є ланцюговою гомотопією між ${\displaystyle g}$ і ${\displaystyle f}$, що доводить симетричність відношення. Якщо ${\displaystyle D_{k}}$ є ланцюговою гомотопією між ланцюговими відображеннями ${\displaystyle f}$ і ${\displaystyle g}$, а ${\displaystyle E_{k}}$ є ланцюговою гомотопією між ланцюговими відображеннями ${\displaystyle g}$ і ${\displaystyle h}$, то ${\displaystyle D_{k}+E_{k}}$ є ланцюговою гомотопією між відображеннями ${\displaystyle f}$ і ${\displaystyle h.}$ Тобто відношення є також транзитивним і, як наслідок, відношенням еквівалентності. Клас еквівалентності ланцюгового відображення ${\displaystyle f}$ позначають ${\displaystyle [f]}$, еквівалентність відображеннь ${\displaystyle f}$ і ${\displaystyle g}$ позначається як ${\displaystyle f\simeq g.}$
• Якщо ${\displaystyle X}$, ${\displaystyle Y}$ і ${\displaystyle Z}$ — ланцюгові комплекси і ${\displaystyle f_{1},g_{1}:X\to Y,\;f_{2},g_{2}:Y\to Z}$ — ланцюгові відображення, такі що ${\displaystyle f_{1}\simeq g_{1},\,f_{2}\simeq g_{2},}$ то також ${\displaystyle f_{2}\circ f_{1}\simeq g_{2}\circ g_{1}.}$ Відповідно можна ввести добуток на класах ланцюгової гомотопії ${\displaystyle [g]\circ [f]=[g\circ f].}$ Якщо для ланцюгового відображення ${\displaystyle f:X\to Y}$ існує таке відображення ${\displaystyle f':Y\to X,}$ що ${\displaystyle f'\circ f\simeq \operatorname {Id} _{X}}$ і ${\displaystyle f\circ f'\simeq \operatorname {Id} _{Y}}$ то ланцюгові комплекси називаються гомотопно еквівалентними.

• Якщо відображення ${\displaystyle f}$ і ${\displaystyle g}$ є ланцюгово гомотопними, то індуковані відображення на гомологічних групах ${\displaystyle H_{k}(X)\to H_{k}(Y)}$ є рівними (де ${\displaystyle H_{k}(X)=\mathrm {Ker} \,d_{X}^{k}/\mathrm {Im} \,d_{X}^{k+1}}$). Справді, нехай ${\displaystyle c\in X_{k}}$ — цикл, тобто елемент з ${\displaystyle \mathrm {Ker} \,d_{X}^{k}}$. Тоді ${\displaystyle d_{X}^{k}(c)=0}$. Так як ${\displaystyle f}$ і ${\displaystyle g}$ є ланцюгово гомотопними, то

  ${\displaystyle f_{k}(c)-g_{k}(c)=D_{k-1}d_{X}^{k}(c)+d_{Y}^{k+1}D_{k}(c)=d_{Y}^{k+1}D_{k}(c)}$,

Тобто відрізняються на границю (елемент ${\displaystyle \mathrm {Im} \,d_{Y}^{k+1}}$).

• Для більшості теорій гомологій гомотопні неперервні відображення топологічних просторів ${\displaystyle f,g\colon X\to Y}$ індукують ланцюгово гомотопні відображення комплексів ${\displaystyle C(X)\to C(Y)}$ і, по доведеному, однакові відображення груп гомологій ${\displaystyle H(X)\to H(Y)}$ (виконується аксіома гомотопічної інваріантності).

• Ланцюговий комплекс

• Вик Дж. У. Теория гомологий. Введение в алгебраическую топологию. — Москва: МЦНМО, 2005 (рос.)
• Гельфанд С. И., Манин Ю. И. Методы гомологической алгебры. Введение в когомологии и производные категории. Том 1. — Москва: Наука, 1989 (рос.)
• Дольд А. Лекции по алгебраической топологии. — Москва: Мир, 1976 (рос.)
• Маклейн С. Гомология. — Москва: Мир, 1966 (рос.)
• Спеньер Э. Алгебраическая топология. — Москва: Мир, 1971 (рос.)