Ланцюговий комплекс

Ланцюговим комплексом називається послідовність ${\displaystyle (K_{\bullet },\partial _{\bullet })}$ модулів і гомоморфізмів ${\displaystyle \partial _{n}:K_{n}\to K_{n-1}}$, що називаються граничними операторами або диференціалами

${\displaystyle \ldots {\xleftarrow {}}K_{n-1}{\xleftarrow {\partial _{n}}}K_{n}{\xleftarrow {\partial _{n+1}}}K_{n+1}{\xleftarrow {}}\ldots }$

така що ${\displaystyle \partial _{n}\partial _{n+1}=0}$. Елементи ${\displaystyle K_{n}}$ називаються n-мірними ланцюгами, елементи ядра ${\displaystyle Z_{n}K=Ker\partial _{n}}$ — n-вимірними циклами, елементи образа ${\displaystyle B_{n}K=Im\partial _{n+1}}$— n-вимірними границями. З ${\displaystyle \partial _{n}\partial _{n+1}=0}$ випливає, що ${\displaystyle B_{n}K\subset Z_{n}K}$ (т.зв. напівточність). Якщо до того ж ${\displaystyle B_{n}K=Z_{n}K}$, то такий комплекс називається точним.

Ланцюгові комплекси модулів над фіксованим кільцем утворюють категорію з мофізмами ${\displaystyle ~\varphi _{\bullet }\colon (K_{\bullet },\partial _{\bullet }^{K})\to (L_{\bullet },\partial _{\bullet }^{L})}$, де ${\displaystyle \varphi _{\bullet }}$ послідовність морфізмів ${\displaystyle \varphi _{n}\colon K_{n}\to L_{n}}$, така що ${\displaystyle \varphi _{n}}$ комутує з диференціалом, тобто ${\displaystyle \partial _{n}^{L}\varphi _{n}=\varphi _{n-1}\partial _{n}^{K}}$.

Коланцюговий комплекс — поняття, двоїсте ланцюговому комплексу. Він визначається як послідовність модулів ${\displaystyle (\Omega ^{\bullet },d^{\bullet })}$ і гомоморфізмов ${\displaystyle d^{n}\colon \Omega ^{n}\to \Omega ^{n+1}}$, таких що

${\displaystyle d^{n+1}d^{n}=0}$

Коцепной комплекс, як і ланцюговий, є напівточною послідовністю.

${\displaystyle \ldots {\xrightarrow {}}\Omega ^{n-1}{\xrightarrow {d^{n-1}}}\Omega ^{n}{\xrightarrow {d^{n}}}\Omega ^{n+1}{\xrightarrow {d^{n+1}}}\ldots }$

Властивості і поняття, пов'язані з коланцюговими комплексами, двоїсті аналогічним поняттям і властивостям ланцюгових комплексів.

n-вимірна група гомологій ${\displaystyle H_{n}}$ ланцюгового комплексу ${\displaystyle (K_{\bullet },\partial _{\bullet })}$ є його мірою точності в n-ому члені і визначається як

${\displaystyle H_{n}(K_{\bullet },\partial _{\bullet })=B_{n}(K)/Z_{n}(K)=\mathrm {Ker} \partial _{n}/\mathrm {Im} ,\partial _{n+1}}$. Для точного комплексу ${\displaystyle H_{n}=0}$

Аналогічно визначається n-вимірна група когомологій коланцюгового комплексу:

${\displaystyle H^{n}(\Omega ^{\bullet },d^{\bullet })=B^{n}/Z^{n}=\mathrm {Ker} d^{n}/\mathrm {Im} ,d^{n-1}}$

Гомоморфізмом ланцюгових комплексів ${\displaystyle (A_{\bullet },\delta _{\bullet })}$ і ${\displaystyle (B_{\bullet },\gamma _{\bullet })}$ називається таке відображення ${\displaystyle f\colon A_{n}\to B_{n},\forall n\in \mathbb {N} ,}$ що наступна діаграма є комутативною:

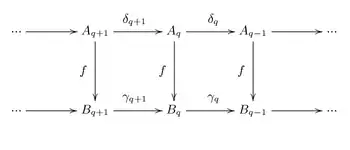
Гомоморфізм ланцюгових комплексів індукує гомоморфізм їх груп гомологій.

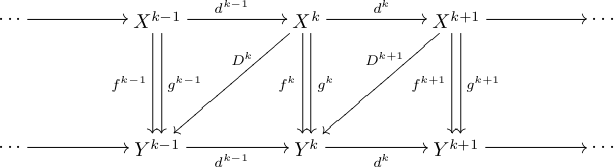
Ланцюгова гомотопія ${\displaystyle D\colon X\to Y}$ між гомоморфізмами комплексів ${\displaystyle f}$ і ${\displaystyle g}$ — гомоморфізм ланцюгових комплексів ${\displaystyle (X_{\bullet },\partial _{\bullet })}$ і ${\displaystyle (Y_{\bullet },\delta _{\bullet })}$ ступеня +1 (тобто ${\displaystyle D_{k}\colon X_{k}\to Y_{k+1}}$), для якого

${\displaystyle \delta D+D\partial =g-f}$

${\displaystyle \delta _{k+1}D_{k}+D_{k-1}\partial _{k}=g_{k}-f_{k}}$

Для коланцюгових комплексів відповідна комутативна діаграма має вигляд.

• Картан А., Эйленберг С. Гомологическая алгебра, — Москва: Издательство Иностранной Литературы, 1960.
• Маклейн С. Гомология, — Москва: Мир, 1966.
• Дольд А. Лекции по алгебраической топологии, — Москва: Мир, 1976.