Лінеаризація

Лінеаризація функції — це дієвий метод для наближеного обчислення значення функції ${\displaystyle y=f(x)}$ в будь-якій ${\displaystyle x=a,}$ беручи за основу нахил функції в ${\displaystyle x=b}$, за умови неперервності ${\displaystyle f(x)}$ на ${\displaystyle [a,b]}$ (або ${\displaystyle [b,a]}$) і того, що ${\displaystyle a}$ достатньо близько до ${\displaystyle b}$. Коротко, лінеаризація обчислює наближене значення функції біля ${\displaystyle x=a}$.

Наприклад, ${\displaystyle {\sqrt {4}}=2}$. Однак, що буде хорошим наближенням для ${\displaystyle {\sqrt {4.001}}={\sqrt {4+.001}}}$?

Будь-яку функцію ${\displaystyle y=f(x)}$ можна лінеаризувати якщо вона неперервна біля цікавої нам точки. Для лінеаризації ${\displaystyle L_{a}(x)}$ функції ${\displaystyle f(x)}$ в точці ${\displaystyle x=a}$ виконується ${\displaystyle L_{a}(a)=f(a)}$. Загальною формою рівняння в околі точки ${\displaystyle (y_{0},x_{0})}$ при нахилі ${\displaystyle M}$ є: ${\displaystyle y-y_{0}=M(x-x_{0})}$.

Використовуючи точку ${\displaystyle (a,f(a))}$, ${\displaystyle L_{a}(x)}$ набуває вигляду ${\displaystyle y=f(a)+M(x-a)}$. Бо неперервні функції є локально лінійні, найкращим нахилом для підстановки буде нахил дотичної до ${\displaystyle f(x)}$ у ${\displaystyle x=a}$.

Наближення для f(x)=x^2 у (x, f(x))

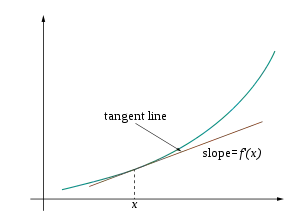
Візуально, на зображені показана дотична лінії для ${\displaystyle f(x)}$ у ${\displaystyle x}$. В ${\displaystyle x+h}$, де ${\displaystyle h}$ є будь-яким достатньо малим по модулю значенням, ${\displaystyle f(x+h)}$ дуже близьке до значення на дотичній в точці ${\displaystyle (x+h,L(x+h))}$.

У результаті отримуємо рівняння для лінеаризації функції в ${\displaystyle x=a}$:

${\displaystyle y=f(a)+f'(a)(x-a)\,}$

Щоб знайти ${\displaystyle {\sqrt {4.001}}}$, ми можемо використати те, що ${\displaystyle {\sqrt {4}}=2}$. Лінеаризацією ${\displaystyle f(x)={\sqrt {x}}}$ в ${\displaystyle x=a}$ є ${\displaystyle y={\sqrt {a}}+{\frac {1}{2{\sqrt {a}}}}(x-a)}$, бо функція ${\displaystyle f'(x)={\frac {1}{2{\sqrt {x}}}}}$ визначає нахил функції ${\displaystyle f(x)={\sqrt {x}}}$ в ${\displaystyle x}$. При ${\displaystyle a=4}$, лінеаризація в 4 є ${\displaystyle y=2+{\frac {x-4}{4}}}$. У цьому випадку ${\displaystyle x=4.001}$, отже ${\displaystyle {\sqrt {4.001}}}$ це приблизно ${\displaystyle 2+{\frac {4.001-4}{4}}=2.00025}$. Справжнє значення близьке до 2.00024998.

Рівняння для лінеаризації функції ${\displaystyle f(x,y)}$ в точці ${\displaystyle p(a,b)}$ таке:

${\displaystyle f(x,y)\approx f(a,b)+\left.{\frac {\partial f(x,y)}{\partial x}}\right|_{a,b}(x-a)+\left.{\frac {\partial f(x,y)}{\partial y}}\right|_{a,b}(y-b)}$

Узагальнене рівняння для лінеаризації функції багатьох змінних ${\displaystyle f(\mathbf {x} )}$ у точці ${\displaystyle \mathbf {p} }$ таке:

${\displaystyle f({\mathbf {x} })\approx f({\mathbf {p} })+\left.{\nabla f}\right|_{\mathbf {p} }\cdot ({\mathbf {x} }-{\mathbf {p} })}$

де ${\displaystyle \mathbf {x} }$ є вектором змінних і ${\displaystyle \mathbf {p} }$ точка в якій ми лінеаризуємо.[1]

Лінеаризація дає можливість розглядати нелінійну систему як лінійну в деякому обмеженому сенсі і таким чином аналізувати її поведінку в околі цікавих нам точок. Зазвичай це критичні точки, тобто такі, де ${\displaystyle \mathbf {F} (\mathbf {x} ,t)=0.}$ Лінеаризація функції це доданок першого порядку з ряду Тейлора біля точки. Отже для системи визначеної рівнянням

${\displaystyle {\frac {d\mathbf {x} }{dt}}=\mathbf {F} (\mathbf {x} ,t)}$,

лінеаризовану систему можна записати як

${\displaystyle {\frac {d\mathbf {x} }{dt}}=\mathbf {F} (\mathbf {x_{0}} ,t)+D\mathbf {F} (\mathbf {x_{0}} ,t)\cdot (\mathbf {x} -\mathbf {x_{0}} )}$

де ${\displaystyle \mathbf {x_{0}} }$ це цікава нам точка і ${\displaystyle D\mathbf {F} (\mathbf {x_{0}} )}$ це якобіан ${\displaystyle \mathbf {F} (\mathbf {x} )}$ evaluated at ${\displaystyle \mathbf {x_{0}} }$.

Якщо точка ${\displaystyle \mathbf {x_{0}} }$   критична, то рівняння набуває вигляду

${\displaystyle {\frac {d\mathbf {x} }{dt}}=\mathbf {J} _{F}(\mathbf {x_{0}} ,t)\cdot (\mathbf {x} -\mathbf {x_{0}} )}$