Математичне моделювання інфекційних захворювань

Першопрохідцями в моделюванні інфекційних захворювань були: Вільям Гамер[1] та Рональд Росс, який на початку XX століття застосував закон дії мас, щоб пояснити поведінку епідемії. Ловелл Рід і Вейд Гемптон Фрост розробили епідемічну модель Reed-Frost, щоб описати зв'язок між сприйнятливими до захворювання, інфікованими і тими що набули імунітету особинами в популяції.

Подальшим розвитком відповідної теорії стала так звана SIR модель, розроблена у 1920-х роках О. Кермаком та Андерсоном Греєм МакКендріком[2].

R₀

середнє число особин популяції, кожна з яких може заразити осіб популяції, які не мають імунітету до цього захворювання.

S

частина особин популяції сприйнятливих до захворювання.

A

середній вік особин популяції, в якому спадає чисельність інфікованих особин для заданої популяції.

L

середня тривалість життя для даної популяції.

Моделі залежать від припущень на яких вони базуються. Якщо отримані результати моделі не відповідають спостереженням і математичне формулювання є коректним, то нам слід змінити початкові умови, щоб мати змогу використати задану модель.

• Прямокутний, стаціонарний розподіл за віком, тобто кожна особина популяції живе до часу L, а потім помирає, також кожна вікова категорія популяції має однакову чисельність. Це часто використовується в розвинутих країнах, де існує низька дитяча смертність і висока тривалість життя.
• Рівномірне змішування популяції, тобто особини популяції вступають в контакт випадковим чином і здебільшого не змішуються в менші підгрупи. Це припущення рідко знаходить своє виправдання, оскільки соціальні структури є широко поширеними. Наприклад, більшість мешканців Лондона вступають в контакт переважно з іншими мешканцями Лондона. Крім того, в Лондоні є менші підгрупи, такі як турецька громада, або спільнота осіб підліткового віку, які змішуються одні з одними набагато більше, ніж поза межами своїх спільнот. Проте однорідне змішування є стандартним припущенням, для того щоб отримати змогу побудувати математичну модель.

Анімована SIR модель поширення інфекційного захворювання

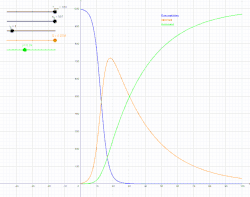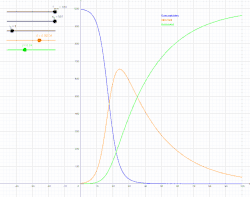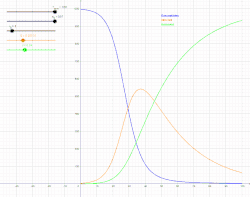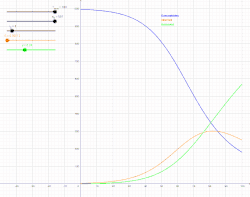
Інфекційна хвороба є ендемічною в популяції, коли ця хвороба постійно підтримується в цій популяції без потреби в зовнішніх джерелах. Це означає, що, в середньому, кожна інфікована особа заражає рівно одну особину (більше того, кількість інфікованих людей буде зростати експоненційно, що спричинить епідемію, проте з часом хвороба спадатиме). В математичних позначеннях, це означатиме, що:

${\displaystyle \ R_{0}\ =1.}$

Коефіцієнт поширення (R₀) захворювання, припускаючи, що кожна особа є сприйнятливою до захворювання, помножений на частку осіб популяції, сприйнятливих до захворювання (S), повинен бути визначеним єдиним чином (тому особини, які не є сприйнятливими до захворювання, не враховуватимуться в обчисленнях, так як вони не можуть бути інфікованими). Зауважимо, для того щоб захворювання перебувало в стані стійкості, необхідно, щоб виконувалось наступне співвідношення: чим більший коефіцієнт поширення захворювання, тим менше число осіб популяції, схильних до захворювання, і навпаки. Припустимо, що заданий прямокутний, стаціонарний розподіл за віком та однакове поширення інфекції на кожну вікову групу популяції. Нехай A — середній вік особин, на яких поширюється інфекція, причому особи молодші за A є сприйнятливими до захворювання, а ті, які старші, — несприйнятливі. Тоді можна показати, що частка осіб популяції, сприйнятливих до захворювання, задається як:

${\displaystyle S={\frac {A}{L}}.}$

Проте, згідно з визначенням стану стійкості ендемічного захворювання:

${\displaystyle S={\frac {1}{R_{0}}}.}$

Тому згідно з транзитивним відношенням:

${\displaystyle {\frac {1}{R_{0}}}={\frac {A}{L}}\Rightarrow R_{0}={\frac {L}{A}}.}$

Використавши вхідні дані, отримуємо простий спосіб оцінки параметра R₀. Для населення з експоненційним віковим розподілом

${\displaystyle R_{0}=1+{\frac {L}{A}}.}$

Це дає змогу обчислити коефіцієнт поширення захворювання для будь-якого розподілу популяції.

Математичні моделі повинні об'єднувати в собі зростаючий об'єм даних, викликаний хост-патогенними взаємодіями. Багато теоретичних досліджень динаміки росту популяцій, структури та еволюції інфекційних захворювань рослин і тварин, включаючи людей, є пов'язаними із цією проблемою. Зокрема є такі напрямки досліджень:

• поширення та контроль захворювання
• епідеміологічні мережі
• просторова епідеміологія
• імунна епідеміологія
• вірулентність
• штам структури і взаємодії
• антигенна мутація
• генетика популяції мікроорганізмів
• роль генетичних чинників хазяїна організму
• статистичні та математичні інструменти та інновації
• роль та ідентифікація місць поширення інфекції

Якщо частка осіб, які мають імунітет до захворювання, перевищує колективний імунітет для цього захворювання, то в цій популяції, інфекція не може поширюватись. Також це співвідношення може бути перевищеним при вакцинації населення, що призводить до усунення хвороби. Прикладом успішного використання вакцинації є подолання спалахів віспи у світі(останній раз глобальний спалах якої був у 1977 році). ВООЗ проводить схожу кампанію вакцинації з викорінення поліомієліту. Позначимо q — рівень колективного імунітету. Нагадаємо, що для стану стійкості:

${\displaystyle \ R_{0}\cdot S=1.}$

S буде рівним (1 − q), оскільки q — частка популяції, яка має імунітет і q + S має бути рівним одиниці(так як в цій спрощеній моделі, кожна особина популяції є або сприйнятливою до захворювання, або має імунітет). Тоді:

${\displaystyle \ R_{0}\cdot (1-q)=1,}$

${\displaystyle 1-q={\frac {1}{R_{0}}},}$

${\displaystyle q=1-{\frac {1}{R_{0}}}.}$

Зауважимо, що рівень колективного імунітету є граничним. Якщо частка осіб з імунітетом перевищує цей рівень, в результаті програми масової вакцинації, хвороба буде відмирати. У проведених вище обчисленнях, ми знайшли поріг критичної імунізації популяції(позначається, як q_c). Це мінімальна частка популяції, яка повинна бути імунізованою при народженні (або близько до народження) для того, щоб інфекція не мала змоги поширюватись в популяції.

${\displaystyle q_{c}=1-{\frac {1}{R_{0}}}}$

• Базове репродуктивне число
• Моделювання екосистем

• Anderson, Roy M.; May, Robert M. Infectious Diseases of Humans. ISBN 0-19-854040-X.
• Keeling, Matt; Rohani, Pej. Modeling Infectious Diseases: In Humans and Animals. Princeton: Princeton University Press.
• Vynnycky, Emilia; White, Richard G. An Introduction to Infectious Disease Modelling. Процитовано 15 лютого 2016. An introductory book on infectious disease modelling and its applications.
• Jenner. Smallpox and its Eradication.
• Riley S (June 2007). Large-scale spatial-transmission models of infectious disease. Science 316 (5829): 1298–301. PMID 17540894. doi:10.1126/science.1134695.

• Institute for Disease Modeling
• Institute for Emerging Infections, University of Oxford
• Center for Infectious Disease Modeling and Analysis, Yale School of Public Health
• Center for Infectious Disease Dynamics, The Pennsylvania State University
• Cambridge Infectious Diseases
• Centre for the Mathematical Modelling of Infectious Diseases, London School of Hygiene & Tropical Medicine
• Models of Infectious Disease Agent Study
• Infectious Disease Modeling: Measles Virus
• Model-Builder: Interactive (GUI-based) software to build, simulate, and analyze ODE models.
• Tuberculosis Modelling and Analysis Consortium (TB MAC): Group focused on improving global Tuberculosis control by coordinating and promoting mathematical modelling and other quantitative research activities.
• GLEaMviz Simulator: Enables simulation of emerging infectious diseases spreading across the world.
• STEM: Open source framework for Epidemiological Modeling available through the Eclipse Foundation.