Метод аналізу ієрархій

Першим кроком у МАІ є моделювання проблеми як ієрархії. Роблячи це, учасники досліджують аспекти проблеми на рівнях від загального до детального, а потім висловлюють її на багаторівневій основі, що вимагає МАІ. Працюючи над побудовою ієрархії, вони покращують своє розуміння проблеми, її контексту, а також думок і почуттів один одного.[26]

Ієрархія — це стратифікована система ранжування та організації людей, речей, ідей тощо, де кожен елемент системи, крім найвищого, підпорядкований одному або декільком іншим елементам. Хоча поняття ієрархії легко сприймається інтуїтивно, його також можна описати математично.[27] Діаграми ієрархій часто мають форму піраміди, але крім необхідності мати один елемент у верхній частині, ієрархії необов'язково мати форму піраміди.

Людські організації часто структуровані як ієрархії, де ієрархічна система використовується для розподілу відповідальності, здійснення керівництва та полегшення спілкування. Знайомі ієрархії «речей» включають в себе системний блок настільного комп'ютера вгорі, з підпорядкованим йому монітором, клавіатурою та мишею «внизу».

У світі ідей ми використовуємо ієрархію, щоб допомогти собі отримати детальне знання складної реальності: ми структуруємо реальність на її складові частини, а вони, в свою чергу, на свої складові частини, рухаючись вниз по ієрархії на стільки рівнів, скільки нам цікаво. На кожному кроці ми зосереджуємось на розумінні окремого компонента цілого, тимчасово нехтуючи іншими компонентами на цьому та всіх інших рівнях. Проходячи цей процес, ми збільшуємо наше глобальне розуміння будь-якої складної реальності, яку ми вивчаємо.

Подумайте про ієрархію, яку використовують студенти-медики під час вивчення анатомії — вони окремо розглядають опорно-руховий апарат (включаючи такі частини та частини, як рука та складові м'язи та кістки), систему кровообігу (та багато її рівнів та гілок), нервову систему (та її численні компоненти та підсистеми) тощо, поки вони не охоплять всі системи та важливі підрозділи кожної. Просунуті студенти продовжують підрозділ аж до рівня клітини або молекули. Зрештою, студенти розуміють «загальну картину» та значну кількість її деталей. Мало того, вони розуміють відношення окремих частин до цілого. Працюючи в ієрархічній формі, вони отримали всебічне розуміння анатомії.

Подібним чином, коли ми підходимо до складної проблеми прийняття рішення, ми можемо використовувати ієрархію, щоб інтегрувати великі обсяги інформації в наше розуміння ситуації. Побудувавши цю інформаційну структуру, ми формуємо все кращу і кращу картину проблеми в цілому.[26]

Ієрархія МАІ є структурованим засобом моделювання відповідного рішення. Вона складається із загальної мети, групи варіантів або альтернатив для досягнення мети та групи факторів або критеріїв, які пов'язують альтернативи з метою. Критерії можуть бути далі розбиті на підкритерії, під-критерії тощо на стільки рівнів, скільки вимагає проблема. Критерій може застосовуватись не однорідно, але, може мати градуйовані відмінності, як-от трохи солодощі приємно, але занадто багато солодощі може завдати шкоди. У цьому випадку критерій поділяється на підкритерії, що вказують на різну інтенсивність критерію, такі як: мала, середня, висока, і ці інтенсивності мають пріоритет через порівняння за батьківським критерієм, солодкість. Опубліковані описи програм МАІ часто включають схеми та описи їх ієрархій; деякі прості показані в цій статті. Більш складні ієрархії МАІ були зібрані та передруковані щонайменше в одній книзі.[28]

Структура будь-якої ієрархії МАІ буде залежати не тільки від характеру розглядуваної проблеми, а й від знань, суджень, цінностей, думок, потреб, потреб тощо учасників процесу прийняття рішень. Побудова ієрархії, як правило, передбачає значні обговорення, дослідження та відкриття учасниками. Навіть після початкової побудови його можна змінити з урахуванням нещодавно продуманих критеріїв або критеріїв, які спочатку не вважалися важливими; альтернативи також можна додавати, видаляти або змінювати.[26]

Щоб краще зрозуміти ієрархію МАІ, необхідно розглянути проблему прийняття рішення з метою, яку потрібно досягти, трьома альтернативними способами досягнення цілі та чотирма критеріями, за якими альтернативи потрібно вимірювати.

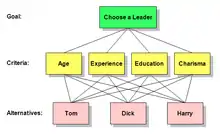
Таку ієрархію можна візуалізувати як схему, подібну до тієї, що знаходиться безпосередньо внизу, з ціллю вгорі, трьома альтернативами внизу та чотирма критеріями між ними. Існують корисні терміни для опису частин таких діаграм: Кожне поле називається вузлом. Вузол, який підключений до одного або декількох вузлів на рівні нижче нього, називається батьківським вузлом. Вузли, до яких він так зв'язаний, називаються його дочірніми.

Застосовуючи ці визначення до наведеної нижче схеми, мета є батьківською для чотирьох критеріїв, а чотири критерії є дочірніми для цілі. Кожен критерій є батьківським для трьох альтернатив. Зверніть увагу, що є лише три альтернативи, але на схемі кожна з них повторюється під кожним із батьківських вузлів.

Проста ієрархія МАІ. Існує три Альтернативи досягнення Цілі та чотири Критерії, які слід використовувати для прийняття рішення серед них.

Щоб зменшити розмір необхідного креслення, зазвичай представляють ієрархії МАІ, як показано на діаграмі нижче, лише з одним вузлом для кожної альтернативи та з декількома лініями, що з'єднують альтернативи та критерії, що застосовуються до них. Щоб уникнути безладу, ці рядки іноді опускають або зменшують кількість. Незалежно від таких спрощень на схемі, у фактичній ієрархії кожен критерій індивідуально пов'язаний з альтернативами. Рядки можна вважати спрямованими вниз від батьків на одному рівні до його дітей на рівні нижче.

Ієрархія МАІ для вибору лідера. Є одна мета, три кандидати та чотири критерії вибору серед них.

Після побудови ієрархії учасники аналізують її через серію попарних порівнянь, які отримують числові шкали вимірювань для вузлів. Критерії попарно порівнюються по важливості для цілі. Альтернативи попарно порівнюються за кожним із критеріїв. Порівняння обробляються математично, а пріоритети виводяться для кожного вузла.

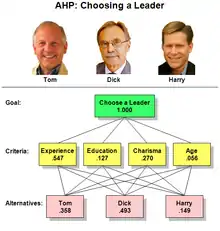
Розглянемо наведений вище приклад «Вибір лідера». Важливим завданням осіб, які приймають рішення, є визначення ваги, яку слід надати кожному критерію при виборі лідера. Іншим важливим завданням є визначення ваги, яку слід додати кожному кандидату з урахуванням кожного з критеріїв. МАІ не лише дозволяє це робити, але і дозволяє надати значуще та об'єктивне числове значення кожному з чотирьох критеріїв.

Пріоритетами є числа, пов'язані з вузлами ієрархії МАІ. Вони представляють відносну вагу вузлів будь-якої групи.

Як і ймовірності, пріоритетами є безрозмірні величини між нулем та одиницею, без одиниць виміру та розмірів. Вузол з пріоритетом 0,200 має вдвічі більшу вагу для досягнення цілі, як той, що має пріоритет 0,100, у десять разів перевищує вагу з пріоритетом 0,020 тощо. Залежно від розглянутої проблеми, «вага» може означати важливість, перевагу, вірогідність або будь-який фактор, який розглядається особами, що приймають рішення.

Пріоритети розподіляються по ієрархії відповідно до її архітектури, і їх значення залежать від інформації, що вводиться користувачами процесу. Пріоритети Цілі, Критеріїв та Альтернативи тісно пов'язані, але їх слід розглядати окремо.

За визначенням, пріоритетом Цілі є 1. Пріоритети альтернатив завжди складають до 1. Речі можуть ускладнитися з кількома рівнями критеріїв, але якщо існує лише один рівень, їх пріоритети також додаються до 1,000. Все це проілюстровано пріоритетами у наведеному нижче прикладі.

Проста ієрархія і призначеними за замовчанням пріоритетами.

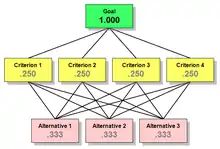
Зауважте, що пріоритети на кожному рівні прикладу — мета, критерії та альтернативи — складають до 1.

Показані пріоритети — це ті, які існують до введення будь-якої інформації про ваги критеріїв чи альтернатив, тому пріоритети на кожному рівні рівні. Їх називають пріоритетами ієрархії за замовчуванням. Якби до цієї ієрархії було додано п'ятий критерій, пріоритетом за замовчуванням для кожного критерію було б 0,200. Якби було лише дві Альтернативи, кожна мала б пріоритет за замовчуванням 0,500.

Дві додаткові концепції застосовуються, коли ієрархія має більше одного рівня критеріїв: місцеві пріоритети та глобальні пріоритети. Розглянемо наведену нижче ієрархію, яка має кілька підкритеріїв за кожним Критерієм.

Більш складна ієрархія МАІ з локальними та глобальними пріоритетами за замовчуванням. З метою ясності альтернативи рішення не відображаються на схемі.

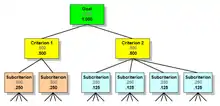
Локальні пріоритети, позначені сірим кольором, представляють відносну вагу вузлів у групі братів і сестер відносно їх батьків. Локальні пріоритети кожної групи Критеріїв та підкритеріїв їх братів і сестер складають до 1,000. Глобальні пріоритети, показані чорним, отримуються шляхом множення локальних пріоритетів братів і сестер на загальний пріоритет їх батьків. Глобальні пріоритети для всіх підкритеріїв рівня складають до 1,000.

Правило таке: у рамках ієрархії глобальні пріоритети дочірніх вузлів завжди складаються із загальним пріоритетом їх батьків. У групі дітей місцеві пріоритети складають до 1,000.

Поки що ми розглядали лише пріоритети за замовчуванням. По мірі просування процесу аналітичної ієрархії пріоритети змінюватимуться від значень за замовчуванням, оскільки особи, що приймають рішення, вводять інформацію про важливість різних вузлів. Вони роблять це, роблячи серію попарних порівнянь.

Для визначення пріоритетів серед варіантів рішень та ваг критеріїв проводяться їх попарні порівняння "кожний-з-кожним" за шкалою у таблиці нижче. Результатом попарних порівнянь є оцінка рівня переваги альтернативи ${\displaystyle A_{i}}$ над ${\displaystyle A_{j}}$.

Якщо у порівнянні альтернатив ${\displaystyle A_{i},A_{j}}$ оцінено перевагу як ${\displaystyle a_{i,j}}$, то при зворотному порівнянні ${\displaystyle A_{i},A_{j}}$ перевага оцінюється обернено ${\displaystyle a_{j,i}={\frac {1}{a_{i,j}}}}$. Перевага при порівнянні альтернативи із самою собою оцінюється як 1.

Результатом попарних порівнянь альтернатив є матриця попарних порівнянь альтернатив ${\displaystyle A_{1}...A_{n}}$ виду:

${\displaystyle {\begin{matrix}&A_{1}...A_{n}\\{\begin{matrix}A_{1}\\...\\A_{n}\end{matrix}}&{\begin{bmatrix}a_{1,1}&...&a_{1,n}\\\\a_{n,1}&...&a_{n,n}\end{bmatrix}}\end{matrix}}}$,

де по головній діагоналі розташовано одиниці, ${\displaystyle a_{j,i}={\frac {1}{a_{i,j}}}}$ та ${\displaystyle a_{j,k}={\frac {a_{i,k}}{a_{i,j}}}}$ [4]

Процедура визначення вагових коефіцієнтів з попарних порівнянь може бути використана як для оцінки пріоритетів самих критеріїв, так і для оцінки альтернатив за результатами попарних порівнянь.

У якості вхідних даних даних приймається матриця попарних порівнянь

${\displaystyle {\begin{matrix}&A_{1}...A_{n}\\{\begin{matrix}A_{1}\\...\\A_{n}\end{matrix}}&{\begin{bmatrix}a_{1,1}&...&a_{1,n}\\\\a_{n,1}&...&a_{n,n}\end{bmatrix}}\end{matrix}}}$

Для матриць попарних порівнянь

значенням вагових коефіцієнтів буде власний вектор матриці, такий що

${\displaystyle {\begin{bmatrix}a_{1,1}&...&a_{1,n}\\\\a_{n,1}&...&a_{n,n}\end{bmatrix}}{\begin{bmatrix}W_{1}\\...\\W_{n}\end{bmatrix}}=n{\begin{bmatrix}W_{1}\\...\\W_{n}\end{bmatrix}}}$

або скорочено ${\displaystyle AW=nW}$ або ${\displaystyle (A-nI)W=0}$, де ${\displaystyle I}$ - одинична матриця. [4]

Розрахунок коефіцієнтів вектора ${\displaystyle W_{i}}$ здійснюється за наступною формулою:

${\displaystyle W_{i}={\frac {\sqrt[{n}]{\prod _{j=1}^{n}a_{i,j}}}{\sum _{i=1}^{n}{\sqrt[{n}]{\prod _{j=1}^{n}a_{i,j}}}}}}$,[29]

тобто ${\displaystyle W_{i}}$ - це нормоване середнє геометричне значень попарних порівнянь по кожному рядку. Слід зауважити, що наведена формула розрахунку власного вектора не є універсальною і спирається на властивості матриці порівнянь: ${\displaystyle a_{j,i}={\frac {1}{a_{i,j}}}}$ та ${\displaystyle a_{j,k}={\frac {a_{i,k}}{a_{i,j}}}}$ [4]

На практиці внаслідок помилок експертів, обмеженості простору можливих значень переваг при попарних порівняннях можливе недотримання властивості ${\displaystyle a_{j,k}={\frac {a_{i,k}}{a_{i,j}}}}$ та навіть транзитивності відношення переваги між альтернативами. Тобто матриця попарних порівнянь стає неузгодженою.

Матриці розміром менше ніж 3x3 завжди узгоджені.

Для перевірки узгодженості матриці порівнянь із значень матриці порівнянь та значень власного вектора будується матриця ${\displaystyle E}$ розміром ${\displaystyle n\times n}$, кожен елемент якої ${\displaystyle \epsilon _{i,j}=a_{i,j}{W_{j} \over W_{i}}}$, де ${\displaystyle i,j=1....n}$.[4]

Далі обчислюється сумма усіх елементів матриці ${\displaystyle E}$

${\displaystyle \lambda _{max}=\sum _{j=1}^{n}\epsilon _{i,j}}$ по кожному рядку, обирається максимальне значення.[4]

Якщо матриця попарних порівнянь була повністю узгоджена, то ${\displaystyle \lambda _{max}=n}$, у іншому випадку ${\displaystyle \lambda _{max}>n}$. [4] Далі обчислюється індекс узгодженості ${\displaystyle \mu ={\left\vert {\lambda _{max}}-n\right\vert \over {n-1}}}$.[4]

Таблиця 2. Значення табличного індексу узгодженості

Розмір матриці (n)	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Табличний індекс (${\displaystyle \mu _{T}}$)	0	0	0,52	0,89	1,11	1,25	1,35	1,40	1,45	1,49	1,52	1,54	1,56	1,58	1,59

Відношення узгодженості (англ. consistency ratio) обчислюється як відношення обчисленого індексу узгодженості ${\displaystyle \mu }$ до табличного індексу ${\displaystyle \mu _{T}}$.[4]

Матриця попарних порівнянь вважається узгодженою, якщо ${\displaystyle \mu /\mu _{T}<0.1}$. Якщо матриця попарних порівнянь не є узгодженою, то необхідно у матриці ${\displaystyle E}$ знайти максимальне значення ${\displaystyle \epsilon _{i,j}}$ і переглянути порівняння альтернатив ${\displaystyle A_{i}}$ та ${\displaystyle A_{j}}$.

Першим кроком у розрахунку пріоритетів альтернатив є попарне порівняння альтернатив за кожним критерієм. Тобто для K критеріїв повинно бути сформовано K матриць попарного порівняння. З матриць попарного порівняння розраховується K векторів ${\displaystyle W^{(k)}={\begin{bmatrix}W_{1}^{(k)}\\...\\W_{n}^{(k)}\end{bmatrix}}}$ ваг з n елементів кожен де (k) означає k-й критерій, n - кількість альтернатив.

З векторів ${\displaystyle W^{(k)}}$формується матриця виду

${\displaystyle {\begin{matrix}&\\{\begin{matrix}A_{1}\\...\\A_{n}\end{matrix}}&{\begin{bmatrix}W_{1}^{(1)}&...&W_{1}^{(k)}\\\\W_{n}^{(1)}&...&W_{n}^{(k)}\end{bmatrix}}\end{matrix}}}$

де кожному рядку відповідає одна альтернатива. Зазначена матриця множиться на вектор вагових коефіцієнтів критеріїв.

${\displaystyle {\begin{bmatrix}W_{1}^{(1)}&...&W_{1}^{(k)}\\\\W_{n}^{(1)}&...&W_{n}^{(k)}\end{bmatrix}}{\begin{bmatrix}W^{(1)}\\...\\W^{(k)}\end{bmatrix}}}$

Результатом буде вектор пріоритетів альтернатив. Альтернатива з найбільшим значенням пріоритету має найбільшу перевагу.[4][29]