Многочлен Лагранжа

Інтерполяцій́ний многочле́н Лагра́нжа — многочлен мінімального степеня, що приймає дані значення у даному наборі точок. Для $n+1$ пар чисел $\ (x_{0},y_{0}),(x_{1},y_{1})\dots (x_{n},y_{n})$ , де всі $\ x_{i}$ різні, існує єдиний многочлен $\ L(x)$ степеня не більшого від $n$ , для якого $\ L(x_{i})=y_{i}$ .

У найпростішому випадку $n=1$ - це лінійний многочлен, графік якого — пряма, що проходить через дві задані точки.

Визначення

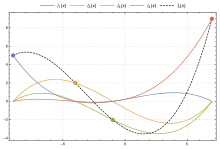
Цей приклад представляє інтерполяційний многочлен Лагранжа для чотирьох точок (-9,5), (-4,2), (-1,-2) і (7,9), а також поліноми y_j l_j(x), кожний з яких проходить через одну з виділених точок, та приймає нульове значення в інших x_i

Лагранж запропонував спосіб обчислення таких многочленів:

L(x)=\sum _{j=0}^{n}y_{j}l_{j}(x)

де базисні поліноми визначаються за формулою:

\ l_{j}(x)=\prod _{i=0,j\neq i}^{n}{\frac {x-x_{i}}{x_{j}-x_{i}}}={\frac {x-x_{0}}{x_{j}-x_{0}}}\cdots {\frac {x-x_{j-1}}{x_{j}-x_{j-1}}}{\frac {x-x_{j+1}}{x_{j}-x_{j+1}}}\cdots {\frac {x-x_{n}}{x_{j}-x_{n}}}\,

Очевидно, що $l_{j}(x)$ мають такі властивості:

Це поліноми степеня $n$
$\ l_{j}(x_{j})=1$
$\ l_{j}(x_{i})=0$ при $i\neq j$

Звідси випливає, що $L(x)$ , як лінійна комбінація $l_{j}(x)$ , може мати степінь не більший від $n$ , та $L(x_{j})=y_{j}$ .

Застосування

Поліноми Лагранжа використовуються для інтерполяції, а також для чисельного інтегрування.

Нехай для функції $f(x)$ відомі значення $y_{j}=f(x_{j})$ у деяких точках. Тоді ця функція може інтерполюватися як

f(x)\approx \sum _{j=0}^{n}f(x_{j})l_{j}(x)

Зокрема,

\int _{a}^{b}f(x)dx\approx \sum _{j=0}^{n}f(x_{j})\int _{a}^{b}l_{j}(x)dx

Значення інтегралів від $l_{j}$ не залежать від $f(x)$ , тож їх можна обчислювати заздалегідь, знаючи послідовність $x_{i}$ .

Для випадку рівномірного розподілу на відрізку вузлів інтерполяції

У вказаному випадку можна виразити $x_{i}$ через відстань між вузлами інтерполяції h та початкову точку $x_{0}$ :

x_{j}\equiv {x_{0}+jh}

,

і, як наслідок,

{x_{i}-x_{j}}\equiv (i-j)h

.

Якщо підставити ці вирази у формулу базисного полінома та винести h за знаки множення у чисельнику та знаменнику, отримаємо

l_{i}(x)={\prod \limits _{j=0,i\neq j}^{n}{(x-x_{j}) \over (x_{i}-x_{j})}}={\prod \limits _{j=0,i\neq j}^{n}(x-x_{0}-jh) \over h^{n-1}\prod \limits _{j=0,i\neq j}^{n}(i-j)}={{{h^{n-1}}\prod \limits _{j=0,i\neq j}^{n}({{x-x_{0}} \over h}-j)} \over {h^{n-1}\prod \limits _{j=0,i\neq j}^{n}(i-j)}}\,\!

.

Після цього можна ввести заміну змінної

y={{\frac {x-x_{0}}{h}}\,\!}

і отримати поліном від у, який будується з використанням лише цілочисленної арифметики. Недоліком цього підходу є факторіальна складність чисельника та знаменника, що вимагає використання алгоритмів з багатобайтним представленням чисел.

Приклади

Приклад 1

Ми бажаємо інтерполювати ƒ(x) = x² на діапазоні 1 ≤ x ≤ 3, із відомими трьома точками:

{\begin{aligned}x_{0}&=1&&&f(x_{0})&=1\\x_{1}&=2&&&f(x_{1})&=4\\x_{2}&=3&&&f(x_{2})&=9.\end{aligned}}

Інтерполяційний многочлен такий:

{\begin{aligned}L(x)&={1}\cdot {x-2 \over 1-2}\cdot {x-3 \over 1-3}+{4}\cdot {x-1 \over 2-1}\cdot {x-3 \over 2-3}+{9}\cdot {x-1 \over 3-1}\cdot {x-2 \over 3-2}\\[10pt]&=x^{2}.\end{aligned}}

Приклад 2

Ми бажаємо інтерполювати ƒ(x) = x³ на діапазоні 1 ≤ x ≤ 3, із відомими трьома точками:

$x_{0}=1\,$	$f(x_{0})=1\,$
$x_{1}=2\,$	$f(x_{1})=8\,$
$x_{2}=3\,$	$f(x_{2})=27\,$

Інтерполяційний многочлен такий:

{\begin{aligned}L(x)&={1}\cdot {x-2 \over 1-2}\cdot {x-3 \over 1-3}+{8}\cdot {x-1 \over 2-1}\cdot {x-3 \over 2-3}+{27}\cdot {x-1 \over 3-1}\cdot {x-2 \over 3-2}\\[8pt]&=6x^{2}-11x+6.\end{aligned}}

Зауваження

Приклад розбіжності інтерполяційного многочлена Лагранжа.

Як видно з побудови, кожен раз коли вузол $x_{k}$ змінюється, всі базові многочлени Лагранжа необхідно перерахувати. Найкращим варіантом інтерполяційного многочлена для практичних (або обчислювальних) цілей є барицентрична форма інтерполяції Лагранжа або поліном Ньютона.

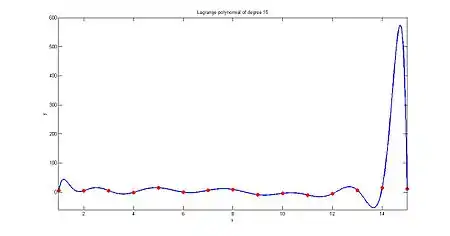
Лагранжева та інші інтерполяції із рівновіддаленими точками, як у прикладах згори, породжують многочлен, що коливається навколо справжньої функції. Ця поведінка сильніше себе виявляє у випадку більшої кількості заданих точок, призводячи до розбіжності відомої як феномен Рунге; проблему можна усунути обравши для інтерполяції вузли Чебишова.

Базові многочлени Лагранжа можна використати у чисельному інтегруванні для виведення формул Ньютона-Котеса.

Приклад реалізації

Код в Oberon

TYPE Point=RECORD x,y:REAL END;

PROCEDURE PolynomLagrange(p:ARRAY OF Point;x:REAL):REAL;
VAR c,s:REAL;
	i,j:INTEGER;
BEGIN
	s:=0;
	FOR i:=0 TO LEN(p)-1 DO
		c := 1;
		FOR j:=0 TO LEN(p)-1 DO
			IF i#j THEN c:=c*(x-p[j].x)/(p[i].x-p[j].x)END
		END;
		s:=s+c*y[i]
	END;
	RETURN s
END PolynomLagrange;

Код в C#

double L_BI_MI(double x)
{
     double r = 0, ra, rb;
     for (int i = 0; i < n; i++)
     {
           ra = rb = 1;
           for (int j = 0; j < n; j++)
               if (i != j)
               {
                   ra *= x - x_[j];    //(x_[i],y_[i]) - інтерполяційні вузли
                   rb *= x_[i] - x_[j];
               }
            r += ra * y_[i] / rb;
    }
    return r;
}

Див. також

Сплайн

Література

ALGLIB has an implementations in C++ / C# / VBA / Pascal.
GSL has a polynomial interpolation code in C
SO has a MATLAB example that demonstrates the algorithm and recreates the first image in this article
Lagrange Method of Interpolation — Notes, PPT, Mathcad, Mathematica, MATLAB, Maple at Holistic Numerical Methods Institute
Lagrange interpolation polynomial on www.math-linux.com

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.