Обгортка (геометрія)
Обгортка сімейства кривих на площині — це крива, що в кожній своїй точці є дотичною хоча б до однієї кривої сімейства і кожним своїм відрізком дотична до нескінченної кількості кривих сімейства[1]. Наприклад, будь-яка гладка крива, що не містить прямолінійних ділянок, буде обгорткою своїх дотичних.
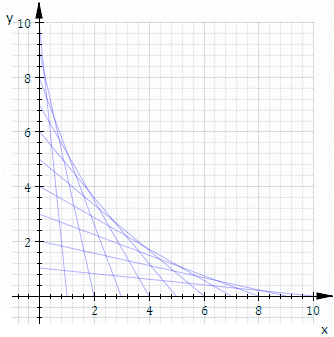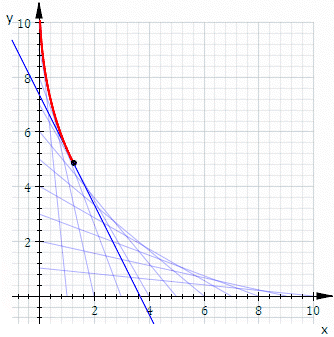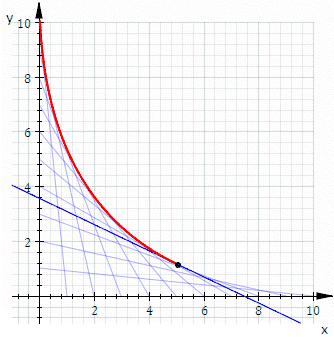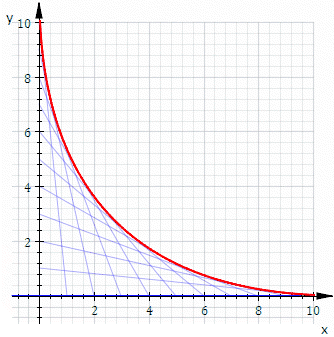
Обгортка сімейства дотичних прямих.
Визначення
Нехай є сімейство гладких кривих , залежне від параметру . Гладка крива буде обвідною сімейства S, якщо[2][1]:
- для кожної точки кривої відповідає крива , дотична до в цій точці,
- для кожної кривої відповідає точка на , в якій дотична до ,
- жодна крива сімейства S не має спільного відрізка з кривою .
Якщо сімейство кривих задано рівнянням . Тоді обгортка сімейства кривих визначається системою
Приклади
- Для сімейства кіл однакового радіуса з центрами на прямій обвідна — це дві паралельні прямі.
- Астроїда є обвідною сімейства відрізків однакової довжини, кінці яких закріплені на двох взаємно-перпендикулярних прямих.
- Парабола є обвідною сімейства серединних перпендикулярів для відрізків, що з'єднують фіксовану точку (фокус параболи) та фіксовану пряму (директрису параболи).
Див. також
Примітки
Посилання
- Weisstein, Eric W. Envelope(англ.) на сайті Wolfram MathWorld.
- «Enveloppe d'une Famille de Courbes Planes» at Encyclopédie des Formes Mathématiques Remarquables
Література
- Борисенко, О. А. Диференціальна геометрія і топологія: Навч. посібник для студ. — Харків : Основа, 1995. — 304 с. — ISBN 5-7768-0388-8.
- Погорєлов О. В. Диференціальна геометрія. — М. : Наука, 1974. — 184 с. — ISBN 5-93972-068-4.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
