Призма (математика)
При́зма (дав.-гр. πρίσμα — «відпиляне»; від πρίζω — «пиляю») — стереометрична фігура, многогранник (призматоїд), у якого дві грані — рівні n-кутники, розташовані в паралельних площинах, а решта n граней — паралелограми. Ці паралелограми називаються бічними гранями призми, а інші два n-кутники називаються її основами.
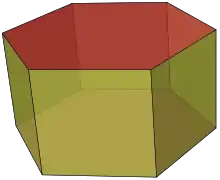
Багатокутник, що лежить в основі, визначає назву призми: трикутник — трикутна призма, чотирикутник — чотирикутна; п'ятикутник — п'ятикутна (пентапризма) і т. д.
Призма є частковим випадком циліндра в загальному сенсі (некругового).
Призма називається прямою, якщо її бічні ребра перпендикулярні до основи. Інші призми — похилі.
Призма називається правильною, якщо вона пряма і її основи — правильні багатокутники.
Висота призми — відстань між площинами її основ.
Види призм
- Призма, основою якої є паралелограм, називається паралелепіпедом.
- Пряма призма — це призма, у якої бічні ребра перпендикулярні до площини основи, звідки випливає, що всі бічні грані є прямокутниками[1]. Інші призми називаються похилими.
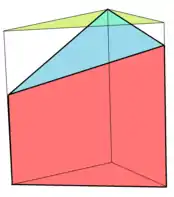 Зрізана трикутна призма
Зрізана трикутна призма - Пряма прямокутна призма називається прямокутним паралелепіпедом. Символ Шлефлі такої призми— { }×{ }×{ }.
- Правильна призма — це пряма призма, основою якої є правильний багатокутник. Бічні грані правильної призми — рівні прямокутники.
- Правильна призма, бічні грані якої є квадратами (висота якої дорівнює стороні основи), є напівправильним багатогранником. Символ Шлефлі такої призми — t{2,p}.
Прямі призми з правильними основами й однаковими довжинами ребер утворюють одну з двох нескінченних послідовностей напівправильних багатогранників, іншу послідовність утворюють антипризми
Зрізана призма — це призма з непаралельними основами[2].
Елементи призми
| Назва | Визначення | Позначення на кресленні | Креслення |
| Основи | Дві грані, є конгруентними багатокутниками, що лежать у паралельних одна одній площинах. | , | 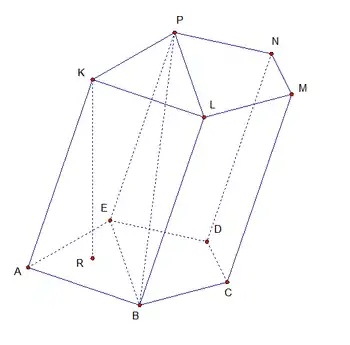 Призма |
| Бічні грані | Усі грані, крім основ. Кожна бічна грань обов'язково є паралелограмом. | , , , , | |
| Бічна поверхня | Об'єднання бічних граней. | ||
| Повна поверхня | Об'єднання основ і бічної поверхні. | ||
| Бічні ребра | Спільні сторони бічних граней. | , , , , | |
| Висота | Відрізок, що з'єднує площини, у яких лежать основи призми і перпендикулярний до цих площин. | ||
| Діагональ | Відрізок, що з'єднує дві вершини призми, які не належать одній грані. | ||
| Діагональна площина | Площина, що проходить через бічне ребро призми і діагональ основи. | ||
| Діагональний переріз | Перетин призми і діагональної площини. В перерізі утворюється паралелограм, зокрема його часткові випадки — ромб, прямокутник, квадрат. | ||
| Перпендикулярний (ортогональний) переріз | Переріз призми і площини, перпендикулярної до її бічного ребра. |
Властивості призми
- Основи призми є рівними багатокутниками.
- Бічні грані призми є паралелограмами.
- Бічні ребра призми паралельні і рівні.
- Об'єм призми дорівнює добутку її висоти на площу основи:
- Об'єм призми з правильною n-кутною основою дорівнює
- (тут s — довжина сторони багатокутника).
- Площа повної поверхні призми дорівнює сумі площі її бічної поверхні і подвоєної площі основи.
- Площа бічної поверхні довільної призми , де — периметр перпендикулярного перерізу, — довжина бічного ребра.
- Площа бічної поверхні прямої призми , де — периметр основи призми, — висота призми.
- Площа бічної поверхні прямої призми з правильною n-кутною основою дорівнює
- Перпендикулярний переріз перпендикулярний до всіх бічних ребер призми.
- Кути перпендикулярного перерізу — це лінійні кути двогранних кутів при відповідних бічних ребрах.
- Перпендикулярний переріз перпендикулярний до всіх бічних граней.
- Двоїстим багатогранником прямої призми є біпіраміда.
Діаграми Шлегеля
 Трикутна призма |
 4-кутна призма |
 5-кутна призма |
 6-кутна призма |
 7-кутна призма |
 8-кутна призма |
Симетрія
Групою симетрії прямої n-кутної призми з правильною основою є група Dnh порядку 4n, за винятком куба, який має групу симетрії Oh порядку 48, що містить три версії D4h в якості підгруп. Групою обертань є Dn 2n, за винятком випадку куба, для якого групою обертань є група O порядку 24, що має три версії D4 в якості підгруп.
Група симетрії Dnh включає центральну симетрію в тому і тільки в тому випадку, коли n парне.
Об'єм
Об'єм призми дорівнює добутку площі основи на висоту. Таким чином об'єм дорівнює:
де S — площа основи, h — висота. Об'єм правильної призми в основі якої є правильний n-кутник дорівнює:
Площа поверхні
Площа бічної поверхні призми дорівнює , де P — периметр основи, H — висота.
Площа поверхні призми дорівнює , де S — площа основи, h — висота, P — периметр основи.
Площа поверхні правильної призми в основі якої є правильний n-кутник дорівнює:
Призматичні багатогранники
Призматичний багатогранник — це узагальнення призми в просторах розмірності 4 і вище. n-вимірний призматичний багатогранник конструюється з двох (n − 1)-вимірних багатогранників, перенесених у наступну розмірність.
Елементи призматичного n-вимірного багатогранника подвоюються з елементів (n − 1)-вимірного багатогранника, потім створюються нові елементи наступного рівня.
Візьмемо n-вимірний багатогранник з елементами (i-вимірна грань, i = 0, …, n). Призматичний ()-вимірний багатогранник буде мати елементів розмірності i (при , ).
За розмірностями:
- Беремо багатокутник з n вершинами і n сторонами. Отримаємо призму з 2n вершинами, 3n ребрами і гранями.
- Беремо багатогранник з v вершинами, e ребрами і f гранями. Отримуємо (4-вимірну) призму з 2v вершинами, ребрами, гранями і комірками.
- Беремо 4-вимірний багатогранник з v вершинами, e ребрами, f гранями і c комірками. Отримуємо (5-вимірну) призму з 2v вершинами, ребрами, (2-вимірними) гранями, комірками гіперкомірками.
Однорідні призматичні багатогранники
Правильний n-багатогранник, представлений символом Шлефлі {p, q, ..., t}, може утворити однорідний призматичний багатогранник розмірності (n + 1), представлений прямим добутком двох символів Шлефлі: {p, q, ..., t}×{}.
За розмірностями:
- Призма з 0-вимірного багатогранника — це відрізок, що подається порожнім символом Шлефлі {}.
- Призма з 1-вимірного багатогранника — це прямокутник, отриманий з двох відрізків. Ця призма подається як добуток символів Шлефлі {}×{}. Якщо призма є квадратом, запис можна скоротити: {}×{} = {4}.
 Приклад: Квадрат, {}×{}, два паралельні відрізки, з'єднані двома іншими відрізками, сторонами.
Приклад: Квадрат, {}×{}, два паралельні відрізки, з'єднані двома іншими відрізками, сторонами.
- багатокутна призма — це 3-вимірна призма, отримана з двох багатокутників (один отриманий паралельним перенесенням іншого), які пов'язані прямокутниками. З правильного багатокутника {p} можна отримати однорідну n-кутну призму, подану добутком {p}×{}. Якщо p = 4, призма стає кубом: {4}×{} = {4, 3}.
 Приклад: п'ятикутна призма, {5}×{}, два паралельні п'ятикутники пов'язані п'ятьма прямокутними сторонами.
Приклад: п'ятикутна призма, {5}×{}, два паралельні п'ятикутники пов'язані п'ятьма прямокутними сторонами.
- 4-вимірна призма, отримана з двох багатогранників (один отримано паралельним перенесенням іншого), зв'язаних 3-вимірними призматичними комірками. З правильного багатогранника {p, q} можна отримати однорідну 4-вимірну призму, подану добутком {p, q}×{}. Якщо багатогранник є кубом і сторони призми теж куби, призма перетворюється на тесеракт: {4, 3}×{} = {4, 3, 3}.
 Приклад: додекаедральна призма, {5, 3}×{}, два паралельні додекаедри, сполучені 12 п'ятикутними призмами (сторонами).
Приклад: додекаедральна призма, {5, 3}×{}, два паралельні додекаедри, сполучені 12 п'ятикутними призмами (сторонами).
- …
Призматичні багатогранники більш високих розмірностей також існують як прямі добутки двох будь-яких багатогранників. Розмірність призматичного багатогранника дорівнює добутку розмірностей елементів добутку. Перший приклад такого добутку існує в 4-вимірному просторі і називається дуопризмами, які отримуються, як добуток двох багатокутників. Правильні дуопризми подаються символом {p}×{q}.
Скручена призма і антипризма
Скручена призма — це неопуклий призматичний багатогранник, отриманий з однорідної q-кутної призми шляхом поділу бічних граней діагоналлю і обертання верхньої основи, зазвичай на кут радіан ( градусів), в напрямку, за якого сторони стають увігнутими[3][4].
Скручена призма не може бути розбита на тетраедри без уведення нових вершин. Найпростіший приклад з трикутними основами називається багатогранником Шенхардта.
Скручена призма топологічно ідентична антипризмі, але має половину симетрій: Dn, [n,2]+, порядку 2n. Цю призму можна розглядати як опуклу антипризму, у якої видалено тетраедри між парами трикутників.
| Трикутна | Чотирикутні | 12-кутна | |
|---|---|---|---|
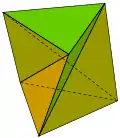 Багатогранник Шенхардта |
 Скручена квадратна антипризма |
 Квадратна антипризма |
 Скручена дванадцятикутна антипризма |
Пов'язані багатогранники і мозаїки
| Багатокутник |  | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Мозаїка | ||||||||||||
| Конфігурація | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 | 17.4.4 | ∞.4.4 |
| n | 2 | 3 | 4 | 5 | 6 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Назва | {2} | t{2} | {3} | t{3} | {4} | t{4} | {5} | t{5} | {6} | t{6} |
| Купол |  Діагональний купол |
 Трискатний купол |
 Чотирискатний купол |
 П’ятискатний купол |
 Шестискатний купол (плоский) | |||||
| Пов'язані однорідні многогранники |
Трикутна призма |
Кубооктаедр |
Ромбокубооктаедр |
Ромбоікосододекаедр |
Ромботришестикутна мозаїка |
Симетрії
Призми топологічно є частиною послідовності однорідних зрізаних багатогранників з конфігураціями вершин (3.2 n.2n) і [n,3].
| Варіанти симетрії *n32 зрізаних мозаїк: 3.2n.2n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симетрія *n32 [n,3] |
Сферична | Евклідова | Компактна гіперболічна | Параком- пактна |
Некомпактна гіперболічна | ||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]… |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | |
| Зрізані фігури |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| Конфігурація | 3.4.4 | 3.6.6 | 3.8.8 | 3.10.10 | 3.12.12 | 3.14.14 | 3.16.16 | 3.∞.∞ | 3.24 i.24i | 3.18 i.18i | 3.12 i.12i |
| Розділені фігури |
 |
 |
 |
 |
 |
 |
|||||
| Конфігурація | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3.∞.∞ | |||
Призми топологічно є частиною послідовності скошених багатогранників з вершинними фігурами (3.4.n.4) і мозаїк на гіперболічній площині. Ці вершиннотранзитивні фігури мають (*n32) дзеркальну симетрію.
| Варіанти симетрії *n42 розширених мозаїк: 3.4.n.4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симетрія *n32 [n,3] |
Сферична | Евклідова | Компактна гіперболічна |
Паракомпактна | ||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]… |
*∞32 [∞,3] | |
| Фігура |  |
 |
 |
 |
 |
 |
 | |
| Конфігурація | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
З'єднання багатогранників
Існує 4 однорідні з'єднання трикутних призм:
- З’єднання чотирьох трикутних призм, з’єднання восьми трикутних призм, з’єднання десяти трикутних призм, з’єднання дванадцяти трикутних призм.
Стільники
Існує 9 однорідних стільників, що включають комірки у вигляді трикутних призм:
- гіроподовжений альтернований кубічний стільник,
- подовжений альтерований кубічний стільник,
- повернутий трикутний призматичний стільник,
- плосконосий квадратний призматичний стільник,
- трикутний призматичний стільник,
- трикутно-шестикутний призматичний стільник,
- зрізаний шестикутний призматичний стільник,
- ромботришестикутний призматичний стільник,
- плосконосий шестикутний призматичний стільник,
- подовжений трикутний призматичний стільник.
Пов'язані багатогранники
Трикутна призма є першим багатогранником в ряду напівправильних багатогранників. Кожен наступний однорідний багатогранник містить в якості вершинної фігури попередній багатогранник. Торольд Госсет ідентифікував цю серію в 1900 як таку, що містить всі фасети правильних багатовимірних багатогранників, всі симплекси і ортоплекси (правильні трикутники і квадрати для випадку трикутних призм). У нотації Коксетера трикутна призма задається символом −121.
| k21 у просторі розмірністю n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Простір | Скінченний | Евклідів | Гіперболічний | ||||||||
| En | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Група Коксетера |
E₃=A₂A₁ | E₄=A₄ | E₅=D₅ | E₆ | E₈ | E₉ = Ẽ₈ = E₈+ | E₁₀ = T₈ = E₈++ | ||||
| Діаграма Коксетера |
|||||||||||
| Симетрія | [3−1,2,1] | [30,2,1] | [31,2,1] | [32,2,1] | [33,2,1] | [34,2,1] | [35,2,1] | [36,2,1] | |||
| Порядок | 12 | 120 | 192 | 51 840 | 2 903 040 | 696 729 600 | ∞ | ||||
| Граф |  |
 |
 |
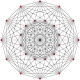 |
 |
 |
- | - | |||
| Позначення | −121 | 021 | 121 | 221 | 321 | 421 | 521 | 621 | |||
Чотиривимірний простір
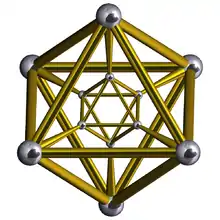
Трикутна призма є коміркою у багатьох чотиривимірних однорідних 4-вимірних багатогранниках, включно з:
| тетраедральна призма |
октаедральна призма |
кубооктаедральна призма |
ікосаедральна призма |
ікосододекаедральна призма |
зрізана додекаедральна призма | ||
 |
 |
 |
 |
 |
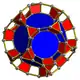 | ||
| ромбоікосі- додекаедральна призма |
ромбокуб- октаедральна призма |
зрізана кубічна призма |
плосконоса додекаедральна призма |
n-кутна антипризматична призма | |||
 |
 |
 |
 |
 | |||
| скошений 5-комірник |
скошено-зрізаний 5-комірник |
обструганий 5-комірник |
струг-зрізаний 5-комірник |
скошений тесеракт |
скошено-зрізаний тесеракт |
обструганий тесеракт |
струг-зрізаний тесеракт |
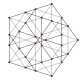 |
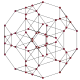 |
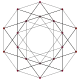 |
 |
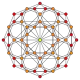 |
 |
 |
 |
| скошений 24-комірник |
скошено-зрізаний 24-комірник |
обструганий 24-комірник |
струг-зрізаний 24-комірник |
скошений 120-комірник |
скошено-зрізаний 120-комірник |
обструганий 120-комірник |
струг-зрізаний 120-комірник |
 |
 |
 |
 |
 |
 |
 |
 |
Примітки
- Kern, Bland, 1938, с. 28.
- Kern, Bland, 1938, с. 81.
- Gorini, 2003, с. 172.
- Малюнки скручених призм
Див. також
Література
- William F. Kern, James R. Bland. Solid Mensuration with proofs. — 1938.
- Catherine A. Gorini. The facts on file: Geometry handbook. — New York : Infobase Publishing, 2003. — (Facts on file). — ISBN 0-8160-4875-4.
- Anthony Pugh. Chapter 2: Archimedean polyhedra, prisma and antiprisms // Polyhedra: A visual approach. — California : University of California Press Berkeley, 1976. — ISBN 0-520-03056-7.
Посилання
- Призма // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 160. — ISBN 978-966-7407-83-4.
- Weisstein, Eric W. Prism(англ.) на сайті Wolfram MathWorld.
- George Olshevsky. «Prismatic polytope». Glossary for Hyperspace.
- Nonconvex Prisms and Antiprisms
- Surface Area MATHguide
- Volume MATHguide
- Paper models of prisms and antiprisms Розгортки призм і антипризм
- Paper models of prisms and antiprisms Розгортки, створені системою Stella.
- Stella: Polyhedron Navigator: Програми для створення 3D- и 4D-зображень, наведених на цій сторінці.
- Гордєєва Є. П. Ч. 1 // Нарисна геометрія. Багатогранники (правильні, неправильні та зірчасті) : навч. посіб. для студ. вищ. навч. закл / Є. П. Гордєєва, В. Л. Величко. — Луцьк : ЛДТУ, 2007. — 191 с. — ISBN ISBN 978-966-7667-70-2.
- Eric W. Weisstein, Prism at MathWorld.

