Перетворення Гільберта

Перетворення Гільберта — лінійне інтегральне перетворення, яке ставить у відповідність функції іншу функцію в тій самій області. Назване на честь Давида Гільберта, який сформулював його в свої роботах над задачею Рімана-Гільберта для голоморфних функцій. Використовується в галузі перетворень Фур'є та аналізу Фур'є. В обробці сигналів перетворення Гільберта перетворює дійсний сигнал на аналітичний.

Перетворення Гільберта прямокутного сигналу.

Визначення

Для дійсних змінних x та y та для дійсних або комплексних функцій f та g перетворення Гільберта визначається як:

g(y)={\mathcal {H}}\left\{{f\left({y}\right)}\right\}={\frac {1}{\pi }}\int _{-\infty }^{\infty }{\frac {f(x)}{y-x}}\mathrm {d} x

Обернене перетворення Гільберта визначається як:

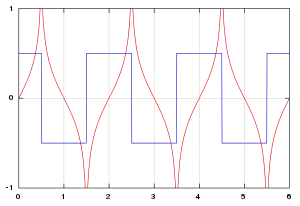
{\mathcal {H}}^{-1}\left\{{g\left({y}\right)}\right\}=-{\mathcal {H}}\left\{{g\left({y}\right)}\right\}=f(y)

Приклади перетворення Гільберта

Сигнал $u(t)\,$	Перетворення Гільберта $H(u)(t)\,$
$\sin(t)\,$	$-\cos(t)\,$
$\cos(t)\,$	$\sin(t)\,$
$1 \over t^{2}+1$	$t \over t^{2}+1$
Функція sinc $\sin(t) \over t$	$1-\cos(t) \over t$
Прямокутна функція $\sqcap (t)$	${1 \over \pi }\ln \left\|{t+{1 \over 2} \over t-{1 \over 2}}\right\|$
Дельта-функція Дірака $\delta (t)\,$	${1 \over \pi t}$
Характеристична функція $\chi _{[a,b]}(x)\,$	${\frac {1}{\pi }}\ln \left\vert {\frac {x-a}{x-b}}\right\vert \,$

Зв'язок з перетворенням Фур'є

Перетворення Фур'є перетворення Гільберта дорівнює:

{\mathcal {F}}({\mathcal {H}}(u))(\omega )=(-i\,\operatorname {sgn} (\omega ))\cdot {\mathcal {F}}(u)(\omega )\,

де ${\mathcal {F}}$ означає перетворення Фур'є, а sgn це Signum-функція.

Згідно з формулою Ейлера,

-i\,\operatorname {sgn} (\omega )\ \,\ =\ {\begin{cases}\ \ i=e^{+i\pi /2},&{\mbox{for }}\omega <0\\\ \ \ \ 0,&{\mbox{for }}\omega =0\\\ \ -i=e^{-i\pi /2}.&{\mbox{for }}\omega >0.\end{cases}}

Отже H(u)(t) здійснює зсув фази компонент негативної частоти u(t) на +90° (π/2 радіан) та фази компонент позитивної частоти на −90°. При цьому i·H(u)(t) відновлює компоненти позитивної частоти та зсуває негативні на додаткові +90°, роблячи їх негативними.

Якщо перетворення Гільберта здійснюється двічі H(H(u)) = −u фаза компонентів негативної та позитивної частоти зсувається на +180° та −180°, відповідно. Сигнал стає негативним оскільки:

e^{\pm i\pi }=-1.

Див. також

Джерела

Bracewell, R. (1986). The Fourier Transform and Its Applications, 2nd ed, McGraw-Hill.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.