Пряма Ньютона
В евклідовій геометрії пряма Ньютона (пряма Гауса) — це пряма, яка проходить через середини діагоналей опуклого чотирикутника, в якому принаймні дві сторони не паралельні[1].
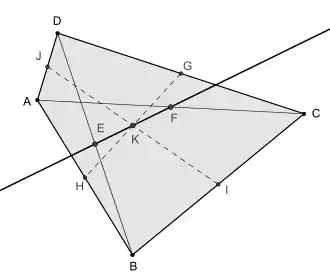
E, K, F лежать на одній прямій, Пряма Ньютона
Властивості
Відрізки GH та IJ, які з'єднують середини протилежних сторін (бімедіани) опуклого чотирикутника, перетинаються в точці, що лежить на прямій Ньютона. Ця точка K ділить навпіл відрізок EF, який з'єднує середні точки діагоналей[1].
За теоремою Енна і навпаки, будь-яка внутрішня точка P на прямій Ньютона чотирикутника ABCD має властивість:
де [ABP] позначає орієнтовану площу трикутника ABP[2].
Якщо чотирикутник є описаним, то його центр вписаного кола також лежить на цій прямій.[3]
Див. також
Джерела
- Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics. MAA, 2010, ISBN 9780883853481, pp. 108—109 (online copy, с. 108, на «Google Books»)
- Сборник статей. Математическое просвещение. Третья серия. Выпуск 11. — Litres, 2015-12-02. — С. 65-66. — ISBN 9785457931350.
- Dušan Djukić, Vladimir Janković, Ivan Matić, Nikola Petrović, The IMO Compendium, Springer, 2006, p. 15.
Посилання
- Weisstein, Eric W. Léon Anne's Theorem(англ.) на сайті Wolfram MathWorld.
- Alexander Bogomolny: Bimedians in a Quadrilateral на cut-the-knot.org
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
