Подерний трикутник

Поде́рний трику́тник (також педа́льний трику́тник і трику́тник проє́кцій[1]) точки $P$ відносно $\triangle ABC$ - це трикутник, вершинами якого є основи перпендикулярів, опущених із точки $P$ на сторони трикутника $ABC$ (або їх продовження).

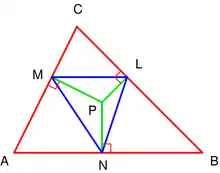
Синій трикутник - подерний трикутник точки

P

відносно червоного трикутника

Пов'язані визначення

Описане коло подерного трикутника називають подерним або педальним колом.
Трикутник із вершинами в інших точках перетину трьох прямих, проведених через вершини подерного трикутника і дану точку $P$ , з описаним колом, називають колово-чевіанним трикутником.

Властивості

Колово-чевіанний трикутник точки подібний до її подерного трикутника.[2].
Вершини подерного трикутника ділть три сторони початкового трикутника на шість відрізків так, що сума квадратів трьох з них, які не мають спільних кінців, дорівнює сумі квадратів трьох інших[3].
- Істинне й зворотне: якщо на трьох сторонах початкового трикутника вибрано три точки так, що вони ділять сторони на шість відрізків, при цьому сума квадратів трьох із них, які не мають спільних кінців, дорівнює сумі квадратів трьох інших, тоді ці три точки є вершинами деякого подерного трикутника[4]. Зокрема:
  - три висоти трикутника перетинаються в одній точці (в ортоцентрі);
  - Три серединних перпендикуляри (медіатриси) до сторін трикутника перетинаються в одній точці (в центрі описаного кола);
  - три перпендикуляри до сторін трикутника, проведені в точках їх дотику з трьома зовнівписаними колами, перетинаються в одній точці.

Окремі випадки подерних трикутників

Вироджений подерний трикутник

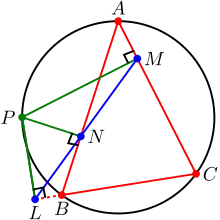
Пряма Сімсона трикутника ABC

Подерний трикутник точки $P$ вироджується в пряму (на малюнку вона синього кольору) тоді і тільки тоді, коли $P$ лежить на описаному колі трикутника $ABC$ . У цьому випадку пряма, що містить подерний трикутник, називається прямою Сімсона.

Рівносторонній подерний трикутник

Подерный трикутник точки Аполлонія є рівностороннім трикутником.

Ортоцентричний трикутник як подерний трикутник

Подерний трикутник ортоцентра є ортоцентричним трикутником.

Серединний трикутник як подерний трикутник

Серединний трикутник (додатковий трикутник) є подерним трикутником центра описаного кола початкового трикутника.

Подерні кола двох ізогонально спряжених точок трикутника

Дві точки трикутника ізогонально спряжені тоді і тільки тоді, коли добутки трьох їхніх відстаней до трьох сторін трикутника рівні[5].
Подерні кола двох ізогонально спряжених точок збігаються[5].
- Зокрема, подерним колом ортоцентра і центра описаного кола (як двох ізогонально спряжених точок трикутника) є коло Ейлера.

Примітки

Зетель, 1962, с. 136.
Задача 108130
Зетель, 1962, с. 137, п. 126, теорема.
Зетель, 1962, с. 136, п. 126, обратная теорема.
Зетель, 1962, с. 97, п. 80.

Література

Зетель С. И. Новая геометрия треугольника. Пособие для учителей. — 2-е издание. — М. : Учпедгиз, 1962.

Посилання

Деякі задачі й теореми про подерний трикутник (рос.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[FOOTNOTEЗетель1962136-1] Зетель, 1962, с. 136.

[2] Задача 108130

[FOOTNOTEЗетель1962137п._126,_теорема-3] Зетель, 1962, с. 137, п. 126, теорема.

[FOOTNOTEЗетель1962136п._126,_обратная_теорема-4] Зетель, 1962, с. 136, п. 126, обратная теорема.

[FOOTNOTEЗетель196297п._80-5] Зетель, 1962, с. 97, п. 80.