Протокол Діффі — Геллмана
Протокол Діффі-Геллмана (англ. Diffie–Hellman key exchange (D–H)[nb 1]) — це метод обміну криптографічними ключами. Один з перших практичних прикладів узгодження ключа, що дозволяє двом учасникам, що не мають жодних попередніх даних один про одного, отримати спільний секретний ключ із використанням незахищеного каналу зв'язку. Цей ключ можна використати для шифрування наступних сеансів зв'язку, що використовують шифр з симетричним ключем.
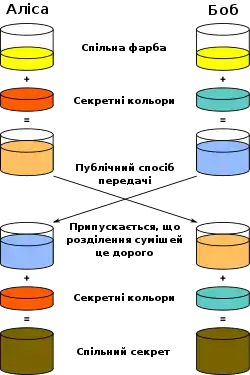 Схематична ілюстрація протоколу на прикладі змішування фарб | |
| Клас | Протокол узгодження ключів |
|---|---|
| Структура даних | Швидкодія та криптографічна стійкість залежать від обраного простору (циклічної групи) |
Схему вперше оприлюднили Вітфілд Діффі і Мартін Геллман у 1976, хоча пізніше стверджувалось, що її кількома роками раніше винайшов Малколм Вільямсон у GCHQ, британській розвідувальній агенції. 2002 року Геллман запропонував називати алгоритм Обмін ключами Діффі-Геллмана-Меркле у визнання внеску Ральфа Меркле в винайденні криптосистем із відкритим ключем.
Хоча протокол Діффі-Геллмана є анонімним (без автентифікації) протоколом встановлення ключа, він забезпечує базу для різноманітних протоколів з автентифікацією, і використовується для забезпечення цілковитої прямої секретності в недовговічних режимах Transport Layer Security (відомих як EDH або DHE залежно від комплектації шифру).
U.S. Patent 4,200,770, термін дії якого наразі вибіг, описує алгоритм і заявляє Геллмана, Діффі і Меркле як винахідників.
Історія
Діффі й Геллман запропонували у 1976 році[1] алгоритм для створення криптографічних систем з відкритим ключем, який так само, як і алгоритм Ель–Гамаля, базується на складності обчислення дискретного логарифма. Алгоритм Діффі–Геллмана може бути використаний для розподілу ключів (генерування секретного ключа), але його не можна використовувати для шифрування повідомлення[2].
Алгоритм узгодження ключа Діффі–Геллмана запатентовано у США та Канаді. Ліцензію на цей патент разом з іншими патентами в області криптографії з відкритим ключем отримала група Public Кеу Partners (PKP). Термін дії патенту США вибіг у 1997 році[2].
Алгоритм Діффі–Геллмана також працює в комутативних кільцях. Шмулі та Кевін МакКерлі запропонували варіант алгоритму, в якому модуль є складеним числом. Міллер і Ніл Кобліц розширили цей алгоритм для використання з еліптичними кривими. Ель–Гамаль використовував основоположну ідею алгоритму Діффі–Геллмана для створення алгоритму шифрування та цифрового підпису. Також є варіант алгоритму для роботи в полі Галуа. У низці реалізацій використаний цей підхід, оскільки обчислення виконуються набагато швидше, але важливо ретельно вибирати поле досить великим, аби забезпечити необхідну стійкість[2].
Криптографічна стійкість алгоритму Діффі–Геллмана заснована на передбачуваній складності проблеми дискретного логарифмування (англ. discrete logarithm problem). Однак, хоча вміння вирішувати проблему дискретного логарифмування дозволить зламати алгоритм Діффі–Хеллмана, зворотне твердження ще не доведене[2].
Необхідно відзначити, що простий алгоритм Діффі–Геллмана працює тільки на лініях зв'язку, надійно захищених від модифікації. Тоді, коли в каналі можлива модифікація даних, з'являється можливість атаки «людина посередині»[2].
Опис алгоритму
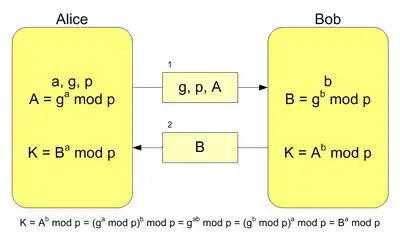
Узгодження спільного таємного ключа відбувається таким чином.
Нехай G — скінченна циклічна група потужністю |G| породжена g[3].
Аліса і Боб таємно обирають два випадкових цілих числа sA та sB, в інтервалі [0, |G| − 1]. Потім вони таємно обчислють числа aA = gsA та aB = gsB відповідно, та обмінюються ними через незахищений канал передачі даних. Нарешті, Аліса та Боб обчислюють aBA = aBsA = gsBsA та aAB = aAsB = gsAsB відповідно. Слід зазначити, що aAB = aBA, і тому це число може служити спільним таємним ключем K Аліси та Боба[3].
Точніше, тепер Аліса та Боб можуть скористатись відображенням елементів множини G у простір іншої криптосистеми. Наприклад, вони можуть використати блок даних необхідного розміру (зокрема, молодші біти) значення aAB як ключ звичайної блочної криптосистеми[3].
Були запропновані варіанти протоколу Діффі-Геллмана для різних множин. Зокрема: мультиплікативні групи над великими скінченними полями (поля простих чисел або розширення), мультиплікативна група залишків за модулем складеного числа, еліптичні криві над скінченними полями, якобіан гіпереліптичних кривих над скінченним полем, та факторгрупи уявних квадратичних полів[3].
Однак, базовий варіант протоколу узгодження ключа анонімний, тут відсутня можливість автентифікації абонентів. Таким чином, протокол вразливий для атаки «людина посередині». Припустімо, що зловмисник C здатен здійснювати підміну повідомлень, якими обмінюються Аліса та Боб. Тоді він може згенерувати числа s*A та s*B, і відповідно, отримати два узгоджених ключа: gsAs*B та gs*AsB. В результаті зловмисник отримує можливість повністю контролювати обмін повідомленнями між Алісою та Бобом. При цьому вони не здатні виявити підміну та вважатимуть, що зв'язуються один з одним[4].
Для розв'язання цієї проблеми були запропоновані підсилені варіанти протоколу. Зокрема[4]:
- Попереднє поширення сертифікатів (англ. static DH),
- Протоколи MTI (за прізвищами авторів англ. Matsumoto, Takashima, Imai),
- Відкритий розподіл ключів із використанням автопідписаних ключів,
- Протокол KEA (англ. Key Exchange Algorithm),
- Протокол «уніфікована модель» (англ. unified model),
- Протокол MQV (автори: англ. Law, Menezes, Qu, Solinas, Vanstone).
З автентифікацією абонентів:
- Протокол STS (англ. station-to-station),
- Протокол DHKE.
Приклад
Єва — криптоаналітик, прослуховувач. Вона читає листування Боба і Аліси, але не може змінити вмісту повідомлень.
- s = секретний ключ. s = 2
- g = відкрите просте число. g = 5
- p = відкрите просте число. p = 23
- a = секретний ключ Аліси. a = 6
- A = відкритий ключ Аліси. A = ga mod p = 8
- b = секретний ключ Боба. b = 15
- B = відкритий ключ Боба. B = gb mod p = 19
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Складність зламу
Постає питання: «Наскільки складно обчислити DH-функцію за умови великого ?» Припустимо, що має біт завдовжки, тоді найліпший з відомих на сьогодні алгоритмів GNFS має час виконання , підекспоненційний час виконання.
Приблизна порівняльна таблиця між складністю злому шифру з різними довжинами ключів і обчисленням функції Діффі-Геллмана в первинному варіанті і в варіанті, коли замість обчислень за модулем використовується інший алгебраїчний об'єкт:
| Розмір ключа шифру | розмір модуля | розмір еліптичної кривої |
|---|---|---|
| 80 | 1024 | 160 |
| 128 | 3072[5] | 256 |
| 256 | 15360 | 512 |
Обчислити функцію Діффі-Геллмана можна через обчислення з і з . Це є проблема дискретного логарифму, яка обчислювальна нерозв'язна при достатньо великих . Обчислення дискретного алгоритму за модулем потребує приблизно стільки ж часу як факторизація добутку двох простих чисел розміру як і , саме на це покладається безпека криптосистем RSA. Отже протокол Діффі-Геллмана приблизно так само безпечний як безпечний RSA[6].
Більше двох учасників
Протокол Діффі-Геллмана не обмежується можливістю узгодження ключа між двома учасниками. Будь-яка кількість учасників може узяти участь в узгоджені ключа через ітеративне виконання протоколу узгодження і обмін проміжними даними (які не мають бути засекреченими). Наприклад, Аліса, Боб і Керол можуть узяти участь в узгоджені так (всі дії відбуваються за модулем ):
- Учасники домовляються про параметри алгоритму і .
- Учасники генерують власні ключі, названі , і .
- Аліса обчислює і відправляє Бобу.
- Боб обчислює і відправляє Керол.
- Керол обчислює і використовує як свій секрет.
- Боб обчислює і відправляє Керол.
- Керол обчислює і відправляє Алісі.
- Аліса обчислює і використовує як свій секрет.
- Керол обчислює і відправляє Алісі.
- Аліса обчислює і відправляє Боб.
- Боб обчислює і використовує як свій секрет.
Підслуховувач може бачити , , , , і , але не здатен використати яку-небудь з комбінацій для відтворення .
Для розширення механізму на більші групи, треба дотримуватись двох засад:
- Починаючи з простого ключа , секрет утворюється піднесенням поточного значення до приватного показника один раз, в будь-якому порядку (перше таке піднесення до степеня дає нам відкритий ключ учасника).
- Будь-яке проміжне значення (яке має до виконаних піднесень до приватних показників, де є число учасників у групі) можна показувати, але кінцеве значення (із застосованими всіма показниками) містить спільний секрет і не може бути оприлюднене. Отже, кожен користувач повинен отримати свою копію спільного секрету застосуванням власного приватного ключа останнім.
Ці принципи залишають відкритими варіанти обрання порядку в якому учасники подають ключі. Найпростіший і найочевидніший розв'язок полягає у впорядкуванні учасників по колу і обійти коло для кожного з них, доки кожен з учасників не зробить внеску в кожен з ключів (з його останнім). Однак, це вимагає від кожного учасника виконати піднесень за модулем.
Через обрання оптимальнішого порядку, і покладання на те, що ключі можуть повторюватись, можливо зменшити кількість піднесень у степінь за модулем виконаних кожним учасником до , через використання підходу розділяй і володарюй, наведеному тут для восьми учасників:
- Кожен з учасників A, B, C і D виконують одне піднесення, породжуючи ; це значення посилається до E, F, G і H. В свою чергу. учасники A, B, C і D отримують .
- Учасники A і B виконують одне піднесення, породжуючи , яке посилається до C і D, а C і D роблять це саме, породжуючи , яке вони посилають до A і B.,
- Учасник A виконує піднесення, породжуючи , яке він посилає B; подібно, B посилає A. C і D чинять подібно.
- Учасник A здійснює одне завершальне піднесення, і отримує секрет , тоді як B робить те саме для отримання ; знову, C і D роблять подібним чином.
- Учасник від E до H одночасно виконують ті самі операції, використовуючи як початкове значення.
По завершені алгоритму, всі учасники володітимуть секретом , але кожен з них виконає лише чотири модульні піднесення, а не вісім, як того потребує просте впорядкування по колу.
Неінтерактивність протоколу
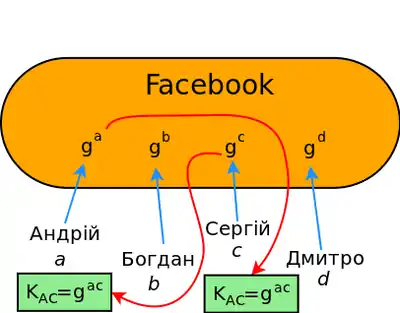
У випадку включення свого внеску до протоколу Діффі-Геллмана до свого відкритого фейсбук-профіля, користувачі не потребують спілкування для узгодження секретного ключа. Одразу по прочитанні відкритого профілю користувача, з ним можна починати безпечний зв'язок. Цю властивість іноді називають властивість неінтерактивності протоколу Діффі-Геллмана.
Чи можемо ми це зробити, також неінтерактивно, для більш ніж двох учасників? Тобто, чи може Андрій прочитати і одразу отримати спільний секретний ключ з Богданом, Сергієм і Дмитром — ? На сьогодні відомо, що це можна зробити для трьох учасників, протокол називається Joux і використовує дуже складну математику. Для більш ніж трьох учасників ця проблема відкрита.
Діффі-Геллман припущення
— скінченна циклічна група порядку . — випадковий породжувач групи. — довільні показники.
CDH
Обчислювальне припущення Діффі-Геллмана (англ. computational Diffie–Hellman assumption):
- — нехтовна мала.
Примітки
- В англомовній літературі зустрічаються такі синоніми:
- Diffie–Hellman key agreement
- Diffie–Hellman key establishment
- Diffie–Hellman key negotiation
- Exponential key exchange
- Diffie–Hellman protocol
- Diffie–Hellman handshake
- W. Diffie and M. E. Hellman, New directions in cryptography, IEEE Transactions on Information Theory, Vol. 22, No. 6 (1976) pp. 644–654.
- М. В. Захарченко, О. В. Онацький, Л. Г. Йона, Т. М. Шинкарчук (2011). 2.11 Алгоритм Діффі–Хеллмана. Асиметричні методи шифрування в телекомунікаціях. ОНАЗ ім. О. С. Попова. ISBN 978-966-7598-71-6.
- Ueli M. Maurer та Stefan Wolf (2000). The Diffie-Hellman Protocol. Des. Codes Cryptography 19 (2/3): 147––171. doi:10.1023/A:1008302122286.
- А.В. Черемушкин (2009). 8.2. Протокол Диффи-Хеллмана и его усиления. Криптографические протоколы. Основные свойства и уязвимости. Академия. с. 173––. ISBN 978-5-7695-5748-4.
- Насправді ніхто не використовує такі великі ключі, використовується значення 2048.
- Weisstein, Eric W. Протокол Діффі-Геллмана(англ.) на сайті Wolfram MathWorld.
Посилання
- Пояснення протоколу Діффі-Геллмана за 5 хвилин на YouTube (англ.)
- RFC 2631 – Метод узгодження ключів Діффі–Геллмана E. Rescorla липень 1999. (англ.)
- Державна служба спеціального зв'язку та захисту інформації України, Наказ № 112: ТЕХНІЧНІ СПЕЦИФІКАЦІЇ форматів криптографічних повідомлень. Захищені дані
