Ректифікація зображення
Ректифікація зображення або вирівнювання — це процес трансформації, який дозволяє спроектувати два або більше зображень в одну спільну площину зображення.
Використовується в:
- комп'ютерному стереобаченні для спрощення задачі пошуку точок відповідності між зображеннями (для вирішення задачі відповідності).
- геоінформаційних система для поєднання зображень відзнятих з різною перспективою в єдину систему координат мапи.
Вирівнювання зображень в комп'ютерному баченні
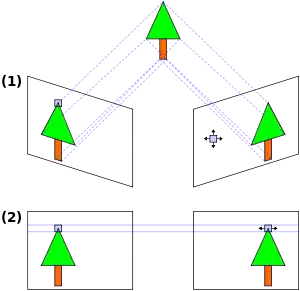
В методах стереобачення використовується триангуляція, що основана на епіполярній геометрії для визначення відстані до об'єкту. Більш конкретно, бінокулярна невідповідність (диспарність) це процес визначення глибини об'єкту відповідно до зміни його позиції при спостереженні з камер в різних точках, де відносна відстань кожної камери відома.
При використанні декількох камер може бути важко точку, яку видно на одному з зображень, визначити на зображенні з іншої камери (відоме як задача відповідності). В більшості конфігураціях камер, відшукання точок відповідності потребує пошуку у двовимірному просторі. Однак, якщо камери розміщено копланарно, пошук спрощується до одного вимірного — по горизонтальній лінії паралельній лінії між камерами. Крім того, якщо положення точки на лівому зображенні відомо, воно може почати пошук на зображенні справа починаючи з цього місця в ліву сторону вздовж прямої, і навпаки (див бінокулярна невідповідність). Вирівнювання зображення є еквівалентом, і частіше за все використовується[1] як альтернатива, ідеального вирівнювання камери. Навіть при дуже точному обладнанні, зазвичай виконують вирівнювання зображення, оскільки може бути практично складно добитися ідеального вирівнювання камер.
Перетворення
Якщо зображення, які необхідно вирівняти відзняті з камер без геометричної дисторсії, це обчислення легко виконати за допомогою лінійного відображення. Обертання довкола X і Y повертає зображення до однієї спільної площини, масштабування дозволяє отримати кадри зображення одного розміру, а обертання довкола осі Z і коригування скосу дозволяє повністю вирівняти рядки пікселів зображення. Потрібно знати точну орієнтацію камер відносно одна одної і коефіцієнти калібрування, які використовуються при трансформування.[2]
Для виконання перетворення, камери самі по собі калібруються для отримання власних параметрів, де основна матриця містить співвідношення між камерами. В більш загальному вигляді (без калібрування камер) вони представлені у вигляді фундаментальної матриці. Якщо фундаментальна матриця не відома, необхідно знайти попередні точки відповідності між стереозображеннями для її знаходження.[2]
Алгоритми
Є три основні категорії алгоритмів вирівнювання зображень: планарне вирівнювання,[3] циліндричне вирівнювання[1] і полярне вирівнювання.[4][5][6]
Деталі реалізації
Ректифіковане зображення повинно задовольняти двом наступним властивостям:[7]
- Всі епіполярні лінії паралельні до горизонтальної осі.
- Відповідні точки мають однакові вертикальні координати.
Для того, щоб перетворити вихідну пару зображень на ректифіковану пару зображень, необхідно знайти проективне перетворення H. На H накладаються умови аби задовольняти вищезгадані властивості. Наприклад, умова що епіполярні лінії мають бути паралельними до горизонтальної осі, означає що епіполюси мають відображатися на нескінченно віддалену точку [1,0,0]T в однорідних координатах. Навіть ці умови, H ще мають чотири степені свободи.[8] Також треба знайти відповідне перетворення H' для ректифікації другого зображення в парі зображень. Невдалий вибір H і H' може призвести до того що ректифіковані зображення мають значні зміни масштабу або серйозно спотворені.
Існує багато різних стратегій вибору проективного перетворенняH для кожного зображення із множини можливих рішень. Одним із прогресивним методом є мінімізація диспарності (невідповідності) або знайдення найменшої квадратичної різниці відповідних точок в горизонтальній осі ректифікованої пари зображень.[8] Інший метод полягає в розділенні H на спеціалізоване проективне перетворення, перетворення подібності і перетворення зсуву (нахилу) для зменшення дисторсії зображення.[7] Одним із простих методів є поворот обох зображень, так що вони виглядають перпендикулярними до лінії, що сполучає їхні загальні оптичні центри, поворот оптичних осей так що горизонтальна вісь кожного малюнку вказує у напрямку оптичного центру іншого зображення, і в кінці масштабується менше зображення так, щоб воно відповідало лінія до лінії іншому зображенню.[9] Цей процес описаний в наступному прикладі.
Приклад
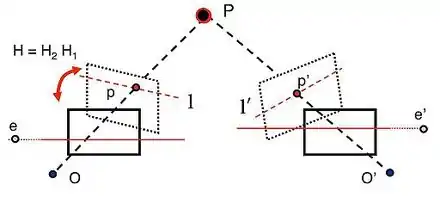
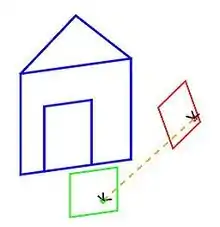
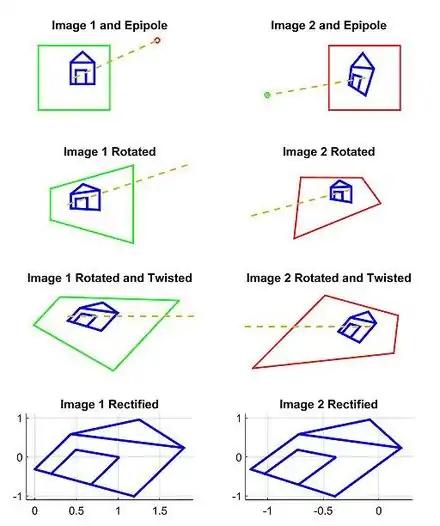
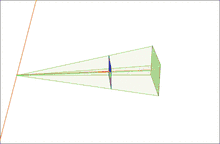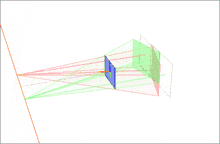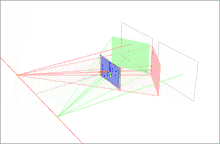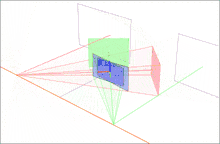
Моделлю для даного прикладу є пара зображень, на яких спостерігається тривимірна точка P, яка відповідає точкам p і p' в координатах пікселів кожного зображення. O і O' є оптичними центрами кожної камери, із відомими матрицями камери і (ми припускаємо що координати реального світу беруться з першої камери). Коротко опишемо і ілюструємо результати простого підходу для вибору проективних перетворень H і H' , які дозволяють ректифікувати пару зображень із прикладу.
Спершу, розрахуємо епіполюси, e і e' кожного зображення:
По друге, знайдемо проективне перетворення H1 яке повертає перше зображення так, що воно буде перпендикулярним до лінії яка сполучає O і O' (рядок 2, стовпець 1 в ілюстрованому наборі 2D зображень). Цей поворот можна обчислити за допомогою векторного добутку між початковою і бажаною оптичною віссю.[9] Потім, ми знаходимо проективне перетворенняH2 яке отримує на вхід повернуте зображення і перекручує його так, що горизонтальна вісь збігається з базовою лінією. Якщо все обраховано вірно, друге перетворення повинно відобразити e на нескінченність на осі x (рядок 3, стовпець 1 в ілюстрованому наборі 2D зображень). І врешті решт, визначимо як проективне перетворення для ректифікації першого зображення.
По третє, за допомогою еквівалентних операцій, ми можемо знайти H' для ректифікації другого зображення (стовпець 2 в ілюстрованому наборі 2D зображень). Відмітимо, що перетворення H'1 повинно повернути друге зображення, так що оптична вісь має бути паралельною із трансформованою оптичною віссю першого зображення. Однією стратегією є підібрати площину паралельну лінії, в якій дві початкові оптичні осі перетинаються для зменшення дисторсії від процесу проектування.[10] В прикладі, ми просто визначаємо H' використовуючи матрицю повороту R і початкове проективне перетворення H як .
В кінці, ми масштабуємо обидва зображення до приблизно однієї роздільної здатності і суміщаємо горизонтальні епіполюси для більш простого горизонтального пошуку відповідностей (рядок 4 в ілюстрованому наборі 2D зображень).
Варто відмітити, що виконати цей і подібні алгоритми можливо не маючи відомих матриць параметрів камери M і M' . Все що тоді потрібно це набір з семи чи більше зображень для обрахунку фундаментальних матриць і епіполюсів із відповідностей зображень.[8]
Геоінформаційні системи
Ректифікація зображення в ГІС системах дозволяє конвертувати зображення у стандартну координатну систему мапи. Це виконується за допомогою зіставлення опорних точок з координатами в із точками зображення. Ці опорні точки використовуються для розрахунку необхідних перетворень зображення.[11]
Основні складності в процесі виникають
- коли точність точок карти не є достатньою
- коли на зображені немає точок, які чітко ідентифікуються і відповідають географічним.
Карти, що використовують вирівняні зображення не є топографічними. Тим не менш, зображення, які використовуються можуть мати спотворення через рельєф. Додаткова орторектифікація усуває цей ефект.[11]
Ректифікація зображень є стандартною функцією програмних пакетів ГІС систем.
Посилання на реалізації
В цьому розділі приводяться посилання на реалізації алгоритмів вирівнювання зображення.
- stereoRectify і stereoRectifyUncalibrated (з використанням OpenCV), мають відкритий код і написані для Windows, Linux/Mac, Android, і iOS
- Rectification Kit і Uncalibrated Rectification Kit, із кодом для MATLAB tutorial, Andrea Fusiello[2]
- rectification, частина на MATLAB package, Du Huynh із коротким описом tutorial[12]
- rectifyStereoImages, функція для MATLAB в Comper Vision System Toolbox
Див. також
Примітки
- Oram, Daniel (2001). Rectification for Any Epipolar Geometry.
- Fusiello, Andrea (17 березня 2000). Epipolar Rectification. Процитовано 9 червня 2008.
- Fusiello, Andrea; Trucco, Emanuele; Verri, Alessandro (2 березня 2000). A compact algorithm for rectification of stereo pairs. Machine Vision and Applications (Springer-Verlag) 12: 16–22. doi:10.1007/s001380050120. Процитовано 8 червня 2010.
- Pollefeys, Marc; Koch, Reinhard; Van Gool, Luc (1999). A simple and efficient rectification method for general motion. Proc. International Conference on Computer Vision: 496–501. Процитовано 2011-01-019.
- Lim, Ser-Nam; Mittal, Anurag; Davis, Larry; Paragios, Nikos. Uncalibrated stereo rectification for automatic 3D surveillance. International Conference on Image Processing 2: 1357. Архів оригіналу за 21 серпня 2010. Процитовано 8 червня 2010.
- Roberto, Rafael; Teichrieb, Veronica; Kelner, Judith (2009). Retificação Cilíndrica: um método eficente para retificar um par de imagens. Workshops of Sibgrapi 2009 - Undergraduate Works (portuguese). Архів оригіналу за 6 липня 2011. Процитовано 5 березня 2011.
- Loop, Charles; Zhang, Zhengyou (1999). Computing rectifying homographies for stereo vision. Computer Vision and Pattern Recognition, 1999. IEEE Computer Society Conference on. Процитовано 9 листопада 2014.
- Richard Hartley and Andrew Zisserman (2003). Multiple view geometry in computer vision. Cambridge university press.
- Richard Szeliski (2010). Computer vision: algorithms and applications. Springer.
- David A. Forsyth and Jean Ponce (2002). Computer vision: a modern approach. Prentice Hall Professional Technical Reference.
- Fogel, David. Image Rectification with Radial Basis Functions. Архів оригіналу за 24 травня 2008. Процитовано 9 червня 2008.
- Huynh, Du. Polar rectification. Процитовано 9 листопада 2014.
Джерела
- Computing Rectifying Homographies for Stereo Vision by Charles Loop and Zhengyou Zhang (April 8, 1999) Microsoft Research