Ряд Лорана

Ряд Лорана — двосторонній[Note 1] степеневий ряд, у який розкладається комплексна функція f(z). Ряди Лорана застосовують для дослідження комплексної функції у тих випадках, коли розклад у ряд Тейлора не може бути застосований. Їх названо на честь П'єра Альфонса Лорана, який уперше опублікував свої дослідження цих рядів 1843 року. Карл Вейєрштрасс, можливо, застосовував такі ряди ще у 1841 році, але не опублікував своїх результатів.

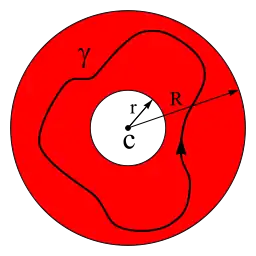
Розклад в ряд Лорана можливий у деякому скінченому кільці, з центром в точці c. Шлях інтегрування γ обирається з кільця, і від вибору того чи іншого шляху інтегрування у фіксованому кільці коефіцієнти розкладу не змінюються.

Для комплексної функції f(z), аналітичної у скінченому кільці з центром у точці c, у довільній точці кільця виконується рівність:

f(z)=\sum _{n=-\infty }^{\infty }a_{n}(z-c)^{n}

де члени ряду a_n визначаються за формулою:

a_{n}={\frac {1}{2\pi i}}\oint _{\gamma }{\frac {f(z)\,dz}{(z-c)^{n+1}}}.\,

Шлях інтегрування γ є довільним замкненим контуром, що лежить у кільці і містить точку с.

Властивості

Головною частиною ряду Лорана називаються члени з від'ємними степенями:

\sum _{n=1}^{\infty }a_{-n}{(z-a)^{(-n)}}

Правильною частиною (Тейлорівською частиною) ряду Лорана називаються члени з невід'ємними степенями:

\sum _{n=0}^{\infty }a_{n}(z-a)^{n}

Якщо ряд Лорана збігається, то його внутрішність області збіжності є кільцем:

D=\{z\in \mathbb {C} |r<|z-a|<R<\infty \}

У своєму кільці збіжності $D$ ряд Лорана збігається абсолютно.

Функція f(z) в певній точці допускає єдиний розклад у ряд Лорана (якщо такий розклад існує).

Теорема Лорана

Функція f(z) однозначна і аналітична в скінченому кільці $D=\{z\in \mathbb {C} |r<|z-a|<R<\infty \}$ в довільній точці цього кільця допускає розклад у збіжний ряд Лорана.

Ряд Лорана є зручним інструментом для оцінки поведінки функції в околі ізольованої особливої точки. Залежно від головної частини ряду, особливу точку визначають як:

усувна особлива точка, якщо головна частина не містить ненульових членів;

простий полюс, якщо головна частина має скінчену кількість членів;

істотно особлива точка, якщо головна частина має нескінчену кількість членів.

Приклади

Знайти розклад в ряд Лорана в точці $z=i$ функції

{\frac {1}{z^{2}+1}}.

Спочатку відзначимо

{\frac {1}{z^{2}+1}}={\frac {1}{(z-i)(z+i)}}.

Далі,

{\frac {1}{z+i}}={\frac {1}{2i+(z-i)}}=-{\frac {i}{2}}{\frac {1}{1-{\frac {i}{2}}(z-i)}}.

Останній дріб може бути розкладений у геометричну прогресію відносно $z-i$ ,

{\frac {1}{1-{\frac {i}{2}}(z-i)}}=1+{\frac {i}{2}}(z-i)+\left({\frac {i}{2}}(z-i)\right)^{2}+\left({\frac {i}{2}}(z-i)\right)^{3}+\cdots

Множимо прогресію на -i/2, і ділимо обидві частини на z - i:

{\frac {1}{z^{2}+1}}=-\left({\frac {i}{2}}\right){\frac {1}{z-i}}-\left({\frac {i}{2}}\right)^{2}-\left({\frac {i}{2}}\right)^{3}(z-i)-\left({\frac {i}{2}}\right)^{4}(z-i)^{2}-\cdots

Як другий приклад можна розкласти в ряд Лорана квадрат вищерозглянутої функції

{\frac {1}{(z^{2}+1)^{2}}}.

Для цього необхідно піднести до квадрата отриману для попереднього прикладу прогресію. Зазвичай, піднесення до степеня нескінченної прогресії є складною операцією. Однак для обчислення перших $n$ членів ряду Лорана, нам достатньо перемножити між собою перші $n$ членів вихідної прогресії:

{\frac {-1}{4(z-i)^{2}}}-{\frac {i}{4(z-i)}}+{\frac {3}{16}}+\cdots

Примітки

Двостророннім називають степеневий ряд, що містить доданки як додатнього, так і від'ємного степеня.

Джерела

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Двостророннім називають степеневий ряд, що містить доданки як додатнього, так і від'ємного степеня.