Середнє логарифмічне

У математиці, середнім логарифмічним називається функція двох невід'ємних чисел, що рівна частці їх різниці та логарифма їх частки. А саме

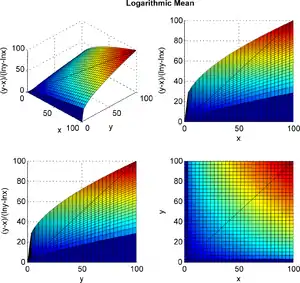
{\begin{array}{ll}M_{\text{lm}}(x,y)&=\lim _{(\xi ,\eta )\to (x,y)}{\frac {\eta -\xi }{\ln \eta -\ln \xi }},\\&={\begin{cases}0&x=0\ \lor \ y=0,\\x&x=y,\\{\frac {y-x}{\ln y-\ln x}}&x\neq y\ \land x,y>0\end{cases}}\end{array}}

Тривимірний графік середнього логарифмічного.

Середнє логарифмічне зокрема використовується для задач теплообміну і масообміну.

Зв'язок з іншими середніми значеннями

Середнє логарифмічне двох чисел є меншим, ніж середнє арифметичне, але більшим, ніж середнє геометричне (коли обидва числа є однаковими, то всі три середні є рівними цьому числу):

{\sqrt {x\cdot y}}\leq M_{\text{lm}}(x,y)\leq {\frac {x+y}{2}}\qquad {\text{ for all }}x\geq 0{\text{ and }}y\geq 0.

<ref>

Ці нерівності можна отримати, наприклад, як наслідок нерівності Ерміта — Адамара.

${\frac {L(x^{2},y^{2})}{L(x,y)}}={\frac {x+y}{2}}$ (Середнє арифметичне)

Інтерпретація в математичному аналізі

Теорема Лагранжа

Із теореми Лагранжа

\exists \xi \in (x,y):\ f'(\xi )={\frac {f(x)-f(y)}{x-y}}

середнє логарифмічне є значенням $\xi$ , якщо за функцію $f$ взяти $\ln$ :

{\frac {1}{\xi }}={\frac {\ln x-\ln y}{x-y}}

і звідси

\xi ={\frac {x-y}{\ln x-\ln y}}.

Інтегрування

Середнє логарифмічне також можна інтерпретувати як площу під експоненційною кривою:

L(x,y)=\int _{0}^{1}x^{1-t}y^{t}\ \mathrm {d} t

${\begin{array}{rcl}\int _{0}^{1}x^{1-t}y^{t}\ \mathrm {d} t&=&\int _{0}^{1}\left({\frac {y}{x}}\right)^{t}x\ \mathrm {d} t\\&=&x\int _{0}^{1}\left({\frac {y}{x}}\right)^{t}\mathrm {d} t\\&=&{\frac {x}{\ln {\frac {y}{x}}}}\left({\frac {y}{x}}\right)^{t}|_{t=0}^{1}\\&=&{\frac {x}{\ln {\frac {y}{x}}}}\left({\frac {y}{x}}-1\right)\\&=&{\frac {y-x}{\ln y-\ln x}}\end{array}}$

Звідси зокрема легко отримати властивість $L(c\cdot x,c\cdot y)=c\cdot L(x,y)$ .

Узагальнення

Через теорему Лагранжа

Середнє логарифмічне можна узагальнити на $n+1$ змінні розглянувши узагальнену теорему Лагранжа для розділених різниць для логарифма $n$ -ї похідної. Тоді можна ввести

L_{\mathrm {MV} }(x_{0},\dots ,x_{n})={\sqrt[{-n}]{(-1)^{(n+1)}\cdot n\cdot \ln[x_{0},\dots ,x_{n}]}}

де $\ln[x_{0},\dots ,x_{n}]$ — розділена різниця логарифму.

Для випадку трьох змінних:

L_{\mathrm {MV} }(x,y,z)={\sqrt {\frac {(x-y)\cdot (y-z)\cdot (z-x)}{2\cdot ((y-z)\cdot \ln x+(z-x)\cdot \ln y+(x-y)\cdot \ln z)}}}

.

Через інтегральний вираз

Узагальнення інтегралу, який дорівнює середньому логарифмічному дає інше узагальнення. Нехай $S$ — симплекс $S=\{(\alpha _{0},\dots ,\alpha _{n}):\alpha _{0}+\dots +\alpha _{n}=1\ \land \ \alpha _{0}\geq 0\ \land \ \dots \ \land \ \alpha _{n}\geq 0\}$ і для деякої міри $\mathrm {d} \alpha$ у якій об'єм симплекса дорівнює 1, отримуємо

L_{\mathrm {I} }(x_{0},\dots ,x_{n})=\int _{S}x_{0}^{\alpha _{0}}\cdot \dots \cdot x_{n}^{\alpha _{n}}\ \mathrm {d} \alpha

За допомогою розділених різниць можна записати

L_{\mathrm {I} }(x_{0},\dots ,x_{n})=n!\cdot \exp[\ln x_{0},\dots ,\ln x_{n}]

.

Для випадку трьох змінних:

L_{\mathrm {I} }(x,y,z)=-2\cdot {\frac {x\cdot (\ln y-\ln z)+y\cdot (\ln z-\ln x)+z\cdot (\ln x-\ln y)}{(\ln x-\ln y)\cdot (\ln y-\ln z)\cdot (\ln z-\ln x)}}

.

Див. також

Література

Niculescu, Constantin P.; Persson, Lars-Erik (2005). Convex Functions and their Applications: A Contemporary Approach. Springer-Verlag. ISBN 0-387-24300-3. Zbl 1100.26002.
Stolarsky, Kenneth B.: Generalizations of the logarithmic mean, Mathematics Magazine, Vol. 48, No. 2, Mar., 1975, pp 87–92

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.