Серія Пашена

Се́рія Паше́на (серія Рітца — Пашена) — спектральна серія у спектрі атома водню, названа на честь німецького фізика Фрідріха Пашена, який 1908 року першим спостерігав лінії цієї серії, до того передбачені швейцарським фізиком-теоретиком Вальтером Рітцем на основі його комбінаційного принципу.
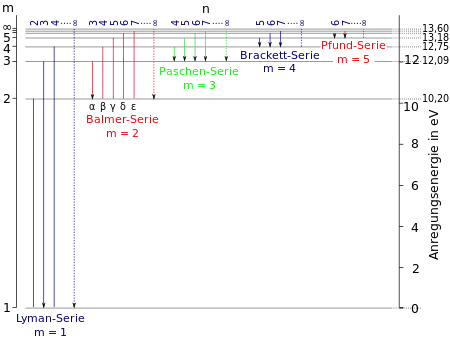
Лінії серії утворюються при переходах електронів між третім та вищими енергетичними рівнями атома водню (у спектрі випромінювання — перехід на третій із вищих рівнів, а у спектрі поглинанні — перехід із третього рівня на розташовані вище).
Для позначення серії застосовується латинська літера P. Переходи позначаються літерами грецької абетки: між третім та четвертим енергетичними рівнями α, між 3-м та 5-м — β і т.д. Таким чином, повне позначення спектральної лінії, що виникає при переході електрона між третім та четвертим рівнями — P_α (вимовляється: «Пашен альфа»).

Основні спектральні серії у спектрі атома водню

Формула Рідберґа для серії Пашена має такий вигляд:

${\displaystyle {1 \over \lambda }=R\left({1 \over 3^{2}}-{1 \over n^{2}}\right),}$

де n — головне квантове число, натуральне число, більше за 3;

${\displaystyle R}$ = 1,0973731568525(73) × 10⁷ м⁻¹.

Усі лінії серії Пашена розташовані в інфрачервоному діапазоні.

Позначення	Pα	Pβ	Pγ	Pδ	Pε	Pζ	Pη	Pθ	Pι	Pκ	...	Межа серії
n	4	5	6	7	8	9	10	11	12	13	...	${\displaystyle \infty }$
Довжина хвилі у повітрі, нм	1875,1	1281,8	1093,8	1004,9	954,6	922,9	901,5	886,3	875,0	866,5		820,4
Довжина хвилі у вакуумі, нм	1875,6	1282,2	1094,1	1005,2	954,9	923,2	901,7	886,5	875,3	866,7		820,6