Скалярна проєкція
У математиці, скалярна проєкція вектора на вектор , яка також називається скалярним компонентом вектора по напрямку вектора , задається у вигляді:
де оператор позначає скалярний добуток, — це одиничний вектор по напрямку , — це довжина вектора , і — кут між і .
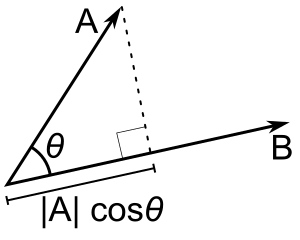
Скалярна проєкція — це скаляр, значення якого дорівнює евклідовій нормі ортогональної проєкції вектора на , і береться зі знаком мінус, якщо проєкція має протилежний напрямок відносно напрямку вектора .
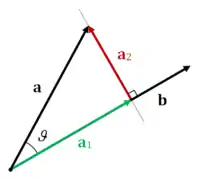
Вектор, отриманий як добуток скалярної проєкції на на одиничний вектор називається векторною проєкцією на .
Визначення засноване на куті θ
Якщо відомий кут між векторами і , то скалярна проєкція на може бути розрахована з використанням такого виразу
Визначення в термінах a і b
Якщо кут не відомий, косинус може бути розрахований через вектори і , використовуючи таку властивість скалярного добутку :
Згідно з цією властивістю, визначення скалярної проєкції буде виглядати таким чином:
Властивості
Скалярна проєкція матиме негативний знак, якщо градусів. Це збігається з відповідною векторною проєкцією евклідової норми, якщо кут менший за 90°. Більш конкретно, якщо векторна проєкція позначається як а її довжина :
- якщо градусів,
- якщо градусів.