Проєкція вектора

Вектор проєкції а на b є вектором, величина якого скалярна проєкція на b і кут, проти b 0 або 180 градусів.

А саме, визначається як: ${\displaystyle \mathbf {a} _{1}=a_{1}\mathbf {\hat {b}} =(|\mathbf {a} |\cos \theta )\mathbf {\hat {b}} }$, де a₁ є відповідна скалярна проєкція, як визначено вище, і b одиничний вектор з тим же напрямком, що і b:

${\displaystyle \mathbf {\hat {b}} ={\frac {\mathbf {b} }{|\mathbf {b} |}}\,}$.

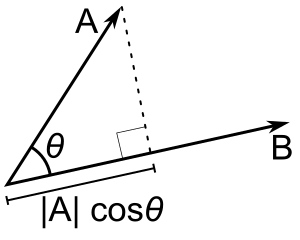
Проєкцією вектора a на інший вектор b є вектор, що обчислюється за формулою

${\displaystyle \mathrm {proj} _{\mathbf {B} }\,(\mathbf {A} )={\frac {\mathbf {A} \cdot \mathbf {B} }{|\mathbf {B} |^{2}}}{\mathbf {B} }.}$

Коли θ невідомо, косинус θ може бути обчислен в термінах а та b

${\displaystyle {\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {a} |\,|\mathbf {b} |}}=\cos \theta \,}$

До вищезазначеної властивості скалярного добутку, визначенням скалярної проєкції стає

${\displaystyle a_{1}=|\mathbf {a} |\cos \theta =|\mathbf {a} |{\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {a} |\,|\mathbf {b} |}}={\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {b} |}}\,}$

Аналогічним чином, визначення вектора проєкції а на b стає

${\displaystyle \mathbf {a} _{1}=a_{1}\mathbf {\hat {b}} ={\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {b} |}}{\frac {\mathbf {b} }{|\mathbf {b} |}},}$

що еквівалентно

${\displaystyle \mathbf {a} _{1}=(\mathbf {a} \cdot \mathbf {\hat {b}} )\mathbf {\hat {b}} ,}$ або[1]

${\displaystyle \mathbf {a} _{1}={\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {b} |^{2}}}{\mathbf {b} }={\frac {\mathbf {a} \cdot \mathbf {b} }{\mathbf {b} \cdot \mathbf {b} }}{\mathbf {b} }.}$

Остання формула є більш ефективною для обчислювання, ніж перша. В кожній з формул потрібно обчислювати скалярний добуток і множити скаляр на вектор, але в першій формулі потрібно додатково обчислювати квадратний корінь та ділити вектор на число.[2], в той час коли в останній потрібно лише розділити скаляр на скаляр.

Відкидання вектора

За визначенням,

${\displaystyle \mathbf {a} _{2}=\mathbf {a} -\mathbf {a} _{1}.}$

Отже,

${\displaystyle \mathbf {a} _{2}=\mathbf {a} -{\frac {\mathbf {a} \cdot \mathbf {b} }{\mathbf {b} \cdot \mathbf {b} }}{\mathbf {b} }.}$

Скалярна проєкція

Скалярний проєкція a на b є скаляр, який має від'ємний знак, якщо 90 < θ ≤ 180 градусів. Вона збігається з довжиною | C | вектора проєкції, якщо кут менше 90 °. Більш точно:

• a₁ = |a₁|, якщо 0 ≤ θ ≤ 90 градусів,
• a₁ = −|a₁|, якщо 90 < θ ≤ 180 градусів.

Векторна проєкція

Вектор проєкція а на b вектор a₁, який є або нульовим або паралельним b. Більш точно:

• a₁ = 0, якщо θ = 90°,
• a₁ та b мають однаковий напрямок, якщо 0 ≤ θ < 90 градусів,
• a₁ and b мають однаковий напрямок, якщо 90 < θ ≤ 180 градусів.

Ортогональна проєкція може бути представлена матрицею проєкції. Для проєктування вектора на одиничний вектор a = (a_x, a_y, a_z), потрібно домножити на проєкцію матриці:

${\displaystyle P_{a}=aa^{\mathrm {T} }={\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}={\begin{bmatrix}a_{x}^{2}&a_{x}a_{y}&a_{x}a_{z}\\a_{x}a_{y}&a_{y}^{2}&a_{y}a_{z}\\a_{x}a_{z}&a_{y}a_{z}&a_{z}^{2}\\\end{bmatrix}}}$

Проєкція вектора є важливою операцією в процесі Грама — Шмідта ортогоналізації векторних космічних баз. Також використовується в теоремі про розділяючу гіперплощину.

Оскільки поняття довжини вектора і кута між векторами може бути узагальненим на будь-якому n-мірному простору, це вірно і для поняття ортогональної проєкції вектора, проєкції вектора на інший, а також відхилення одного вектора від іншого. У деяких випадках, скалярний добуток збігається з добутком точки. Всякий раз, коли вони не збігаються, то скалярний добуток використовується замість скалярного добутку в формальному визначенні проєкції та відхиленні.

Для отримання тривимірного внутрішнього простору, поняття проєкції вектора на інший і відхилення вектора від іншого може бути узагальнено на поняття проєкції вектора на площину, і відхилення вектора від площини.

Проєкція вектора на площині є її ортогональною проєкцією на цю площину. Відхилення вектора від площини є її ортогональною проєкцією на прямій лінії, ортогональної до цієї площини. Обидва вектора, по-перше, паралельно площині, по-друге ортогонально. Для даного вектора і площини, сума проєкції і відхилення дорівнює вихідному вектору.

Так само для  внутрішніх  просторів у більш ніж трьох вимірах, поняття  проєкції на вектор  та відхилення від вектора можна узагальнити на поняття проєкції на гіперплощину, і відхилення від гіперплощини.

• Скалярний добуток
• Скалярна проєкція

• Скалярний добуток і проєкція вектора із прикладами