Список груп сферичної симетрії

Групи сферичної симетрії також називають точковими групами в тривимірному просторі, однак у цій статті розглянуто тільки скінченні симетрії. Існує п'ять фундаментальних класів симетрії, притаманних трикутним фундаментальним областям: діедральна, циклічна, тетраедральна, октаедральна та ікосаедральна симетрія.

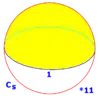Точкова група в тривимірному просторі

Симетрії-інволюції
Cs, (*)
[ ] =
Циклічна симетрія
Cnv, (*nn)
[n] =
Діедральна симетрія
Dnh, (*n22)
[n,2] =
Групи багатогранників, [n,3], (*n32)

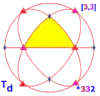Тетраедральна симетрія
Td, (*332)
[3,3] =
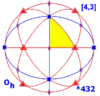Октаедральна симетрія
Oh, (*432)
[4,3] =
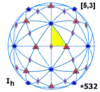Ікосаедральна симетрія
Ih, (*532)
[5,3] =

В статті перелічено групи згідно з символами Шенфліса, нотацією Коксетера[1], орбіфолдною нотацією[2] і порядком. Конвей використовував варіант запису Шенфліса, заснований на алгебраїчній структурі групи кватерніонів, з позначеннями однією або двома великими літерами і повним набором нижніх числових індексів. Порядок групи позначається індексом, якщо тільки він не подвоюється символом плюс-мінус («±»), який передбачає центральну симетрію [3].

Також наведено символіку Германа — Могена (міжнародна нотація). Групи кристалографії, загалом 32, є підмножиною з елементами порядку 2, 3, 4 і 6[4].

Симетрії-інволюції

Є чотири симетрії, які є оберненими собі, тобто інволюціями: тотожне перетворення (C1), дзеркальна симетрія (Cs), обертова симетрія (C2), і центральна симетрія (Ci).

Міжн. Геом.

[5]

 Орб. Шенф. Конвей Кокс. Пор. Фунд.
область
1 1 11 C1 C1 ][
[ ]+		 1
2 2 22 D1
= C2		 D2
= C2		 [2]+ 2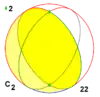
Міжн. Геом. Орб. Шенф. Конвей Кокс. Пор. Фунд.
область
1 22 × Ci
= S2		 CC2 [2+,2+] 2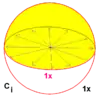
2
= m		 1 * Cs
= C1v
= C1h		 ±C1
= CD2		 [ ] 2


Циклічна симетрія

Існують чотири нескінченних сімейства циклічної симетрії з n=2 і вище (n може дорівнювати 1 як особливий випадок немає симетрії).

Міжн. Гео Орб. Шенф. Конвей Кокс. Пор. Фунд.

область

2 2 22 C2
= D1		 C2
= D2		 [2]+
[2,1]+		 2
mm2 2 *22 C2v
= D1h		 CD4
= DD4		 [2]
[2,1]		 4
4 42 2× S4 CC4 [2+,4+] 4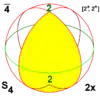
2/m 22 2* C2h
= D1d		 ±C2
= ±D2		 [2,2+]
[2+,2]		 4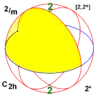
Міжн. Геом. Орб. Шенф. Конвей Кокс. Пор. Фунд.
область
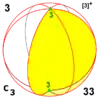
3
4
5
6
n		 3
4
5
6
n		 33
44
55
66
nn		 C3
C4
C5
C6
Cn		 C3
C4
C5
C6
Cn		 [3]+
[4]+
[5]+
[6]+
[n]+
 3
4
5
6
n
3m
4mm
5m
6mm
-		 3
4
5
6
n		 *33
*44
*55
*66
*nn		 C3v
C4v
C5v
C6v
Cnv		 CD6
CD8
CD10
CD12
CD2n		 [3]
[4]
[5]
[6]
[n]		 6
8
10
12
2n
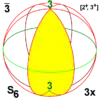
3
8
5
12
-		 62
82
10.2
12.2
2n.2		 3×
4×
5×
6×
n×		 S6
S8
S10
S12
S2n		 ±C3
CC8
±C5
CC12
CC2n / ±Cn		 [2+,6+]
[2+,8+]
[2+,10+]
[2+,12+]
[2+,2n+]		 6
8
10
12
2n
3/m=6
4/m
5/m=10
6/m
n/m		 32
42
52
62
n2		 3*
4*
5*
6*
n*		 C3h
C4h
C5h
C6h
Cnh		 CC6
±C4
CC10
±C6
±Cn / CC2n		 [2,3+]
[2,4+]
[2,5+]
[2,6+]
[2,n+]		 6
8
10
12
2n


Діедральна симетрія

Існує три нескінченних сімейства з діедральною симетрією з n рівним 2 і більше (n може дорівнювати 1 як особливий випадок).

Міжн. Геом. Орб. Шенф. Конвей Кокс. Пор. Фунд.
область
222 2.2 222 D2 D4 [2,2]+ 4
42m 42 2*2 D2d DD8 [2+,4] 8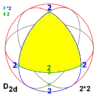
mmm 22 *222 D2h ±D4 [2,2] 8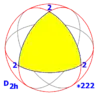
Міжн. Геом. Орб. Шенф. Конвей Кокс. Пор. Фунд.
область
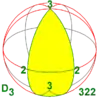
32
422
52
622		 3.2
4.2
5.2
6.2
n.2		 223
224
225
226
22n		 D3
D4
D5
D6
Dn		 D6
D8
D10
D12
D2n		 [2,3]+
[2,4]+
[2,5]+
[2,6]+
[2,n]+		 6
8
10
12
2n
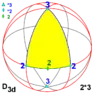
3m
82m
5m
12.2m
 62
82
10.2
12.2
n2
 2*3
2*4
2*5
2*6
2*n		 D3d
D4d
D5d
D6d
Dnd		 ±D6
DD16
±D10
DD24
DD4n / ±D2n		 [2+,6]
[2+,8]
[2+,10]
[2+,12]
[2+,2n]		 12
16
20
24
4n
6m2
4/mmm
10m2
6/mmm		 32
42
52
62
n2		 *223
*224
*225
*226
*22n		 D3h
D4h
D5h
D6h
Dnh		 DD12
±D8
DD20
±D12
±D2n / DD4n		 [2,3]
[2,4]
[2,5]
[2,6]
[2,n]		 12
16
20
24
4n

Симетрії багатогранників

Існує три типи симетрії багатогранників: тетраедральна симетрія, октаедральна симетрія і ікосаедральна симетрія, названі за правильними багатогранниками з трикутними гранями, які мають відповідні симетрії.

Тетраедральна симетрія
Міжн. Геом. Орб. Шенф. Конвей Кокс. Пор. Фунд.
область
23 3.3 332 T T [3,3]+
= [4,3+]+		 12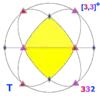
m3 43 3*2 Th ±T [4,3+] 24
43m 33 *332 Td TO [3,3]
= [1+,4,3]		 24
Октаедральна симетрія
Міжн. Геом. Орб. Шенф. Конвей Кокс. Пор. Фунд.
область
432 4.3 432 O O [4,3]+
= [[3,3]]+		 24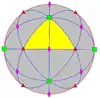
m3m 43 *432 Oh ±O [4,3]
= [[3,3]]		 48
Ікосаедральна симетрія
Міжн. Геом. Орб. Шенф. Конвей Кокс. Пор. Фунд.
область
532 5.3 532 I I [5,3]+ 60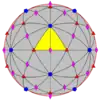
532/m 53 *532 Ih ±I [5,3] 120

Див. також

Примітки
  1. Johnson, 2015.
  2. Conway, 2008.
  3. Conway, 2009.
  4. Sands, 1993.
  5. Hestenes, Holt, 2007.

Література
  • Peter R. Cromwell, Polyhedra (1997), Appendix I
  • Donald E. Sands. Crystal Systems and Geometry // Introduction to Crystallography. — Mineola, New York : Dover Publications, Inc, 1993. — С. 165. — ISBN 0-486-67839-3.
  • Джон Х. Конвей, Дерек А. Смит. О кватернионах и октавах = On Quaternions and Octonions. — Москва : МЦНМО, 2009. — ISBN 978-5-94057-517-7.
  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. The Symmetries of Things. — New-York : A K Peters/CRC Press,, 2008. — ISBN 978-1-56881-220-5.
  • H.S.M. Coxeter. Kaleidoscopes: Selected Writings of H.S.M. Coxeter / F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss,. — Wiley-Interscience Publication,, 1995. — ISBN 978-0-471-01003-6.
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380—407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559—591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
  • Norman Johnson. Chapter 11: Finite symmetry groups // Geometries and Transformations. — 2015.
  • D. Hestenes, J. Holt. The Crystallographic Space groups in Geometric algebra // Journal of Mathematical Physics. — 2007. — Вип. 48, 023514 (3 листопада).

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.