Стаціонарна точка
В математичному аналізі, стаціонарна точка це такий аргумент функції при якому її похідна (градієнт для функції багатьох аргументів) дорівнює нулю.
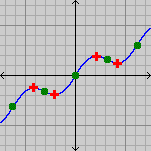
Для графіка одновимірної функції, це відповідає точці, в якій дотична до графіка паралельна осі x. Для графіка двовимірної функції - дотична площина паралельна площині xy.
Термін зазвичай використовується в двох вимірах, те й буде об'єктом даної статті. Стаціонарні точки в вищих розмірностях зазвичай називаються критичними; тому дивіться їх для опису властивостей вищих розмірностей.
Стаціонарні та критичні точки
Термін "критична точка" часто плутають з терміном "стаціонарна точка". Критична точка - загальніший термін: критична точка може бути або стаціонарною або точкою в якій похідна не визначена.
Стаціонарна точка завжди критична, але критична точка не завжди стаціонарна: вона також може бути недиференційовною.
Для гладкої функції ці терміни взаємозамінні, тому і з'явилась плутанина.
Зауважте що існує також інше визначення критичної точки в вищих розмірностях, коли матриця Якобі не має повного рангу, але не обов'язково нульова, це не аналогічно стаціонарним точкам, бо функція все ще може змінюватись в певному напрямку.
Класифікація
Ізольовані стаціонарні точки лінійно-неперервної функції поділяються на чотири види перевіркою першої похідної:
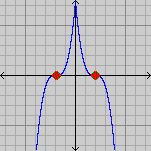
- локальний мінімум - точка в якій похідна функції змінює знак з від'ємного на додатній.
- локальний максимум - точка в якій похідна змінює знак з додатнього на від'ємний.
- зростаюча точка перегину точка в околі якої похідна функції додатня з обох сторін стаціонарної точки. В ній відбувається зміна опуклості
- спадна точка перегину точка в околі якої похідна від'ємна з обох сторін стаціонарної точки. Вона теж змінює опуклість.
Зауваження: Глобальні екстремуми згідно з теоремою Ферма, можуть бути на межі інтервалу або в критичних точках, і не обов'язково мають бути стаціонарними.