Степінь графу

У теорії графів, графом k-степені Gk неорієнтованого графу G є інший граф, що має таку ж саму кількість вершин, але дві його вершини є суміжними, коли відстань між ними не перевищує k. Аналогічну термінологію використовують при піднесенні чисел до степеня: G2 називається G квадрат, G3 називається G куб, тощо.[1]

Квадрат графу

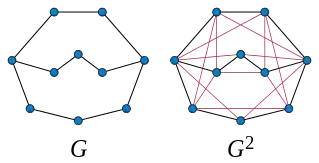
Степінь графу слід відрізняти від добутку графу на себе, який (на відміну від графу в степені) має набагато більше вершин, ніж початковий граф.

Властивості

Якщо граф має діаметр d, то його граф d-степені — повний граф.[2]

Розфарбовування

Розфарбовування квадрату графу може бути використано для розподілення учасників бездротової  мережі зв'язку таким чином, щоб ніякі два учасники не заважали один одному чи спільним сусідам,[3] та для того, щоб виявити візуалізацію графу з найбільшим кутом розширення.[4]

Хроматичне число та виродження планарного графу степені k максимального ступеня Δ дорівнює , де оцінка виродження відображає, що для розфарбування графу такою великою кількістю кольорів може бути використаний алгоритм жадібної розмальовки. Для окремого випадку квадрата планарного графу у 1977 році Вегнер висловив припущення, що хроматичне число квадрату планарного графу не перевищує , так само відомо, що хроматичне число не перевищує .[5][6] Взагалі, для будь-якого графу з виродженням d та максимальним степенем Δ, виродження квадрату графу дорівнює O(dΔ), тож для багатьох з щільних графів, окрім планарних, так само хроматичне число квадрату пропорційне Δ.

Незважаючи на те, що хроматичне число квадрату непланарного графу може бути пропорційним (у найгіршому випадку) Δ, воно буде меншим для графів з великим обхватом, обмежених у цьому випадку O(Δ2/log Δ).[7]

Визначення мінімальної кількості кольорів, необхідних для розфарбування квадрат графу є NP-складною задачею, навіть у випадку з планарним графом.[8]

Гамільтоновість

Куб кожного зв'язного графу обов'язково містить Гамільтонів цикл.[9] Але квадрат зв'язного графу не обов'язково є гамільтоновим, і це є NP-повною задачею — виявити, чи є квадрат гамільтоновим.[10] Проте, за теоремою Флеішнера, квадрат зв'язного графу на дві вершини завжди є гамільтоновим.[11]

Складність обчислення

Граф степені k, що має n вершин і m ребер може бути обчислений за О(mn) часу, за допомогою виконання пошуку в ширину, починаючи з кожної вершини для визначення відстані до всіх інших вершин. Як альтернатива, якщо А — матриця суміжності для графу, у якому змінені усі нульові елементи на головній діагоналі (на ненулеві), то ненулеві елементи матриці Ак дають матрицю суміжності графу степеня k, з цього випливає, що побудова степені k може бути здійснена за той час, що знаходиться у межах логарифмічного фактору часу для множення матриць.

Поняття степені листа тісно пов'язано з k-степенем дерева, індуковане листям дерева G. Цей клас графів знайшов застосування у філогенезі.[12]

Було досягнуто першого твердого результату: Маючи граф, вирішити, чи є квадрат іншого графу NP-повною задачею.[13] Крім того, NP-повною задачею є визначити, чи є граф степенем іншого графу коли k ≥ 2 , чи є він k-степенем двочастинного графу при k>2.[14]

Примітки
  1. Bondy, Andrian; Murty, U.S.R. (2008). Graph Theory (English). Springer: Graduate Texts in Mathematics 244. с. 82. ISBN 9781846289699.
  2. Weisstein, Eric W.. Graph Power. MathWorld.
  3. Agnarsson, Geir; Magnús, M. (2000). "Coloring powers of planar graphs". San Francisco, California: Proceedings of the Eleventh Annual ACM-SIAM Symposium on Discrete Algorithms (SODA '00). с. 654–662.
  4. Formann, M.; Hagerup, T.; Haralambides, J.; Kaufmann, M.; Leighton, F.; Symvonis, A.; Welzl, E.; Woeginger, G. (1 жовтня 1993). Drawing Graphs in the Plane with High Resolution. SIAM Journal on Computing 22 (5). с. 1035–1052. ISSN 0097-5397. doi:10.1137/0222063. Процитовано 30 березня 2016.
  5. Kramer, Florica; Kramer, Horst (6 лютого 2008). A survey on the distance-colouring of graphs. Discrete Mathematics 308 (2–3). с. 422–426. doi:10.1016/j.disc.2006.11.059. Процитовано 30 березня 2016.
  6. Molloy, Michael; Salavatipour, Mohammad R. (1 липня 2005). A bound on the chromatic number of the square of a planar graph. Journal of Combinatorial Theory, Series B 94 (2). с. 189–213. doi:10.1016/j.jctb.2004.12.005. Процитовано 30 березня 2016.
  7. Alon, Noga; Mohar, Bojan (1 січня 2002). The Chromatic Number of Graph Powers. Combinatorics, Probability and Computing 11 (01). с. 1–10. ISSN 1469-2163. doi:10.1017/S0963548301004965. Процитовано 30 березня 2016.
  8. Agnarsson та Halldórsson, (2000) list publications proving NP-hardness for general graphs by McCormick (1983) and Lin and Skiena (1995), and for planar graphs by Ramanathan and Lloyd (1992, 1993).
  9. Bondy та Murty, (2008), p. 105.
  10. Underground, Paris (1978). On graphs with Hamiltonian squares. Discrete Mathematics 21 (3): 323. MR 522906. doi:10.1016/0012-365X(78)90164-4..
  11. Diestel, Reinhard (2012). 10. Hamiltonian cycles. Graph Theory (вид. corrected 4th electronic)..
  12. Nishimura, Naomi; Ragde, Prabhakar; Thilikos, Dimitrios M. (2002). On graph powers for leaf-labeled trees. Journal of Algorithms 42 (1): 69–108. MR 1874637. doi:10.1006/jagm.2001.1195..
  13. Motwani, R.; Sudan, M. (1994). Computing roots of graphs is hard. Discrete Applied Mathematics 54: 81–88. doi:10.1016/0166-218x(94)00023-9..
  14. Le, Van Bang; Nguyen, Ngoc Tuy (2010). Hardness results and efficient algorithms for graph powers. Graph-Theoretic Concepts in Computer Science: 35th International Workshop, WG 2009, Montpellier, France, June 24-26, 2009, Revised Papers. Lecture Notes in Computer Science 5911. Berlin: Springer. с. 238–249. ISBN 978-3-642-11408-3. MR 2587715. doi:10.1007/978-3-642-11409-0_21.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.