Візуалізація графів

Зображення графів знаходиться на перетині математики та комп'ютерних наук, тому, що об'єднує геометричну теорію графів з візуалізацією інформації для отримання двовимірних зображень графів, що виникають в практичних задачах аналізу соціальних мереж, картографії, лінгвістики, та біоінформатики[1].

Графічне представлення всесвітньої мережі за одну хвилину через гіперпосилання

Зображення графу або мережевої діаграми — це графічне представлення вершин та ребер графу. Зображення не слід плутати з самим графом: зовні дуже різні зображення можуть відповідати одному і тому ж графу[2]. З точки зору теорії, все, що має значення — це які саме пари вершин з'єднуються ребрами. Однак, у конкретних ситуаціях, розташування вершин і ребер в межах малюнка впливає на його зрозумілість, зручність використання, вартість виготовлення та на естетичне сприйняття[3]. Задача стає більш складною, якщо граф змінюється з часом, коли додаються і видаляються ребра (зображення динамічного графу), або мета полягає у збереженні мапи думок користувача[4].

Домовленості
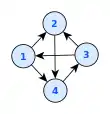
Орієнтований граф з кінцями, що вказують на напрям ребра

Графи зазвичай зображуються як діаграми, що наголошують на зв'язках між вузлами, де вершини представлені у вигляді дисків, коробок або текстових міток, і ребер, зображених відрізками, ламаними або кривими в евклідовому просторі[3]. Такі діаграми можна побачити у роботах 13-го століття Раймунда Луллія, які він використовував для зображення повних графів, з метою аналізу усіх попарних комбінацій для множини метафізичних понять[5].

У випадку орієнтованих графів стрілки вживаються для зазначення їх орієнтації[2]; Проте, дослідження користувачів показали, що використання такого способу, як звуження, цю інформацію надає ефективніше[6]. Висхідне планарне креслення використовує домовленість, що кожне ребро орієнтується від нижчої до вищої вершини, що робить непотрібним зображення кінцівок стріл[7].

  • Альтернативні домовленості використовують такі уявлення суміжності, як пакування кіл, де вершини представлені у вигляді областей в площині, що не перетинаються, а ребра зображені як примикання між областями.
  • Зображення перетинів, в яких вершини зображені, як геометричні об'єкти, що не перетинаються, а ребра — їх перетинами.
  • Зображення видимості, в яких вершини представлені областями в площині, а ребра областями, що мають безперешкодну пряму видимість одне одного.
  • Зображення зливання, на яких ребра — гладкі, криві в межах математичних залізничних колій.
  • Зображення у вигляді тканини, де вершини представлені у вигляді горизонтальних ліній, а ребра у вигляді вертикальних ліній[8].
  • Зображення матриці суміжності графу.

Критерії якості

Багато різних критеріїв якості були визначені для креслень графу в спробі знайти об'єктивний спосіб оцінки їх естетичності та практичності[9]. Крім спрямування вибору між різними методами компонування для графу, деякі методи компонування намагаються безпосередньо оптимізувати ці заходи.

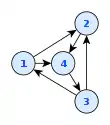
Планарний граф зображений без перетинів ребер
  • Числом схрещувань креслення є число пар ребер, що перетинаються між собою. Якщо цей граф є планарним, то часто буває зручно зобразити його без будь-яких перетинів ребер; тобто, в такому випадку, графік являє собою граф вкладення. Однак неплоскі графи часто виникають у додатках, тому алгоритми малювання графу, як правило, повинні дозволяти перетин ребер[10].
  • Площина зображення — це найменша територія вікна обмеження графу, щодо найближчої відстані між будь-якими двома вершинами. Креслення з меншою площею, як правило, краще, ніж з більшою площею, бо вони дозволяють зберегти особливості малюнка, що будуть показані в більшому розмірі й, отже, більш розбірливо. Співвідношення сторін обмежувального блоку також може бути важливим.
  • Симетрія зображення — це проблема пошуку груп симетрії у даному графі, і знаходження зображення, що є найбільш симетричним. Деякі методи розташування автоматично ведуть до симетричних зображень; з іншого боку, деякі методи зображення починаються зі знаходження симетрії отриманого графу для його зображення[11].
  • Важливо, що ребра мають якомога простішу форму, аби оку людини було легше їх відстежувати. У полілінійних кресленнях, важкість конструкції ребра може вимірюватися у кількості згинів, і багато методів мають на меті надати креслення з невеликою кількістю загальних згинів або кількома згинами на ребро. Подібним чином для сплайн-кривих складність ребра може бути виміряна кількістю контрольних точок на ребрі.
  • Кілька популярних критеріїв якості, пов'язаних з довжиною ребер: в загальному випадку бажано звести до мінімуму загальну довжину країв, а також максимальну довжину будь-якого краю. Крім того, для довжин ребер може бути кращим залишатися однаковими, а не різноманітними.
  • Кутова розрізнювальна здатність — це міра найгострішого кута у зображенні графу. Якщо граф має вершини з великими степенями, то він обов'язково матиме не велику кутову розрізнювальну здатність, але кутова розрізнювальна здатність може бути обмежена знизу функцією степеня[12].
  • Кількість нахилів графу — це мінімальна кількість різних нахилів, що потрібні для зображення прямими лініями ребер сегмента (з перетином). Кубічний граф має кількість нахилів не більше чотирьох, але граф з п'яти кутами може мати необмежену кількість нахилів; ще залишається не зрозумілим, чи обмежена кількість нахилів 4-кутного графу[12].

Методи макетування
Силова візуалізація мережі.[13]

Існує багато стратегій компонування графів:

  • У системі силового компонування, програми зображення графів змінюють початкове розміщення вершин шляхом безперервного переміщення вершин відповідно до системи сил, заснованої на фізичних метафорах, пов'язаних з системами пружин або молекулярної механіки. Зазвичай, ці системи поєднують в собі сили тяжіння між сусідніми вершинами з силами відштовхування між усіма парами вершин, щоб знайти макет, в якому довжини ребер малі, в той час, як вершини добре розділені. Ці системи можуть виконувати метод найшвидшого спуску на основі мінімізації з функції енергії, або ж вони можуть перевести свої сили безпосередньо у швидкості або прискорення для рухомих вершин[14].
  • Метод спектрального макета використовує власні вектори матриці, такі як Лапласів отриманого з матриці суміжності графу[15].
  • Ортогональні методи компонування, що дозволяють ребрам графу йти горизонтально або вертикально, паралельно осям координат макета. Ці методи були спочатку розроблені для схем надвеликого рівня інтеграції, друкованих плат і проблем компонування, але вони також були пристосовані до зображення графів. Вони зазвичай включають багатофазний підхід, в якому введення графу вирівнюється шляхом заміни точок перетину вершинами, знаходиться топологічне вкладення планаризованного графу, орієнтація сторін вибирається так, щоб звести до мінімуму вигини, вершини розташовуються послідовно з цими орієнтаціями, і, нарешті, етап ущільнення макету зменшує площу малюнка[16].
  • Алгоритми макету дерев використовують для зображення деревоподібних структур з коренем, зокрема, це пасує для дерев. Зазвичай, у техніці, що називається «кульовий макет» (англ. balloon layout), нащадок кожного вузла у дереві малюється на колі, що оточує вузол, із радіусом цих кіл, що спадає на нижчих рівнях дерева так, щоб ці кола не накладалися одне на одного[17].
  • Методи багаторівневого зображення графу (які часто називають зображеннями у стилі Сугияма) найкраще підходять для орієнтованого ациклічного графу або графів, близьких до ациклічних, таких як графи залежностей між модулями або функціями в програмній системі. У цих методах, вузли графу розташовані на горизонтальних шарах з використанням методів, таких як алгоритм Коффмана-Грекхема, таким чином, що більшість ребер йдуть вниз від одного шару до іншого; після цього кроку вузли в кожному шарі розташовуються з метою мінімізації перетинів[18].
Дугова діаграма графу
  • Дугова діаграма, це стиль компонування, відомий з 1960-х років[19], розташуємо вершини в одну лінію; ребра можуть бути зображені як півкола вище або нижче лінії, або як плавні криві, з'єднані з декількох півкіл.
  • У круговій схемі вершини обережно розташовані по колу, з метою зменшення перетинів та розташування сусідніх вершин якомога ближче одне до одного. Ребра можуть бути зображені як хорди кола чи його арки зсередини або зовні. Іноді можуть бути використані декілька кіл[20].
  • У макеті переважання вершини записуються таким чином, що кожна вершина знаходиться вище, справа, або з обох боків від іншої, тоді й тільки тоді, коли вона досяжна з цієї вершини. Таким чином, стиль макета робить відношення досяжності графу візуально очевидним[21].

Графічні креслення для конкретних додатків

Графи та зображення графу, що виникають в інших областях застосування, включають:

Крім того, розміщення та трасування — кроки автоматизації проєктування електроніки (EDA) схожі у багатьох аспектах до зображення графів, оскільки існує проблема жадібних вкладень у розподілених обчисленнях, та література з зображення графів містить декілька результатів, позичених з літератури EDA. Однак, ці проблеми також різняться у деяких важливих аспектах: наприклад, у EDA, область мінімізації та довжина сигналу важливіші за естетичність, але проблеми зв'язку у EDA можуть мати понад два термінали на мережу у той час, як аналогічна проблема у зображенні графу зазвичай містить пари вершин для кожного ребра.

Програмне забезпечення

Програмне забезпечення, системи та провайдери систем для малювання графів:

  • BioFabric[8], програма з відкритим вихідним кодом від Інституту біологічних систем для зображення великих мереж шляхом малювання вузлів у вигляді горизонтальних ліній.
  • Cytoscape, програмне забезпечення з відкритим вихідним кодом для візуалізації мереж молекулярної взаємодії.
  • Gephi, програмне забезпечення для аналізу та візуалізації мережі з відкритим кодом.
  • graph-tool — безкоштовна бібліотека Python для аналізу графів.
  • Graphviz, система для малювання графів з відкритим вихідним кодом від AT&T Corporation[28].
  • Linkurious, програмне забезпечення для комерційного аналізу та візуалізації мережі для графових баз даних.
  • Mathematica, засіб обчислення загального призначення, що містить 2D і 3D візуалізації графу та інструменти аналізу графу[29][30].
  • Microsoft Automatic Graph Layout, бібліотека .NET (раніше називалася GLEE) з відкритим кодом для зображення графів[31].
  • NetworkX — це бібліотека Python для вивчення графів та мереж.
  • Tom Sawyer Software[32] Tom Sawyer Perspectives — це графічне програмне забезпечення для візуалізації та аналізу даних та зображення графів корпоративного класу. Це набір для розробки програмного забезпечення із графічним дизайном та середовищем попереднього перегляду.
  • Tulip (software)[33] — інструмент візуалізації даних з відкритим кодом.
  • yEd, редактор графів з функціоналом розмітки[34].
  • PGF/TikZ 3.0 з graphdrawing пакетом (необхідно мати LuaTeX)[35].
  • LaNet-vi, програмне забезпечення для візуалізації великих мереж з відкритим кодом.
  • Edraw Max 2D програмне забезпечення для технічного діаграмування бізнесу.

Посилання
Виноски
  1. Di Battista та ін., (1994), pp. vii–viii; Herman, Melançon та Marshall, (2000), Section 1.1, «Typical Application Areas».
  2. Di Battista та ін., (1994), p. 6.
  3. Di Battista та ін., (1994), p. viii.
  4. Misue та ін., (1995)
  5. Knuth, Donald E. (2013). Two thousand years of combinatorics. У Wilson, Robin; Watkins, John J. Combinatorics: Ancient and Modern. Oxford University Press. с. 7–37..
  6. Holten та van Wijk, (2009); Holten та ін., (2011).
  7. Garg та Tamassia, (1995).
  8. Longabaugh, (2012).
  9. Di Battista та ін., (1994), Section 2.1.2, Aesthetics, pp. 14–16; Purchase, Cohen та James, (1997).
  10. Di Battista та ін., (1994), p 14.
  11. Di Battista та ін., (1994), p. 16.
  12. Pach та Sharir, (2009).
  13. Published in Grandjean, Martin (2014). La connaissance est un réseau. Les Cahiers du Numérique 10 (3): 37–54. doi:10.3166/lcn.10.3.37-54. Процитовано 15 жовтня 2014.
  14. Di Battista та ін., (1994), Section 2.7, «The Force-Directed Approach», pp. 29–30, and Chapter 10, «Force-Directed Methods», pp. 303—326.
  15. Beckman, (1994); Koren, (2005).
  16. Di Battista та ін., (1994), Chapter 5, «Flow and Orthogonal Drawings», pp. 137—170; (Eiglsperger, Fekete та Klau, 2001).
  17. Herman, Melançon та Marshall, (2000), Section 2.2, «Traditional Layout — An Overview».
  18. Sugiyama, Tagawa та Toda, (1981); Bastert та Matuszewski, (2001); Di Battista та ін., (1994), Chapter 9, «Layered Drawings of Digraphs», pp. 265—302.
  19. Saaty, (1964).
  20. Doğrusöz, Madden та Madden, (1997).
  21. Di Battista та ін., (1994), Section 4.7, «Dominance Drawings», pp. 112—127.
  22. Scott, (2000); Brandes, Freeman та Wagner, (2014).
  23. Di Battista та ін., (1994), pp. 15-16, and Chapter 6, «Flow and Upward Planarity», pp. 171—214; Freese, (2004).
  24. Zapponi, (2003).
  25. Anderson та Head, (2006).
  26. Di Battista та Rimondini, (2014).
  27. Bachmaier, Brandes та Schreiber, (2014).
  28. «Graphviz and Dynagraph — Static and Dynamic Graph Drawing Tools», by John Ellson, Emden R. Gansner, Eleftherios Koutsofios, Stephen C. North, and Gordon Woodhull, in Jünger та Mutzel, (2004).
  29. GraphPlot Mathematica documentation
  30. Graph drawing tutorial
  31. Nachmanson, Robertson та Lee, (2008).
  32. Madden та ін., (1996).
  33. «Tulip — A Huge Graph Visualization Framework», by David Auber, in Jünger та Mutzel, (2004).
  34. «yFiles — Visualization and Automatic Layout of Graphs», by Roland Wiese, Markus Eiglsperger, and Michael Kaufmann, in Jünger та Mutzel, (2004).
  35. Tantau, (2013); see also the older GD 2012 presentation
Загальні посилання
Спеціалізовані підтеми

Посилання
  • GraphX library for .NET: WPF бібліотека з відкритим кодом для обчислення та візуалізації графів. Підтримує багато макетів та алгоритмів з'єднання сторін.
  • Graph drawing e-print archive: включає інформацію на папері з усього симпозіуму з зображення графів.
  • Візуалізація графів, каталог посилань Open Directory Project для багатьох додаткових посиланнь, що зв'язані з візуалізацією графів.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.