Суперформула

Суперформула — узагальнений випадок рівняння плоскої кривої супереліпса (кривої Ламе), записаний у 1997 році бельгійським вченим Йоханом Джилісом (англ. Johan Gielis).

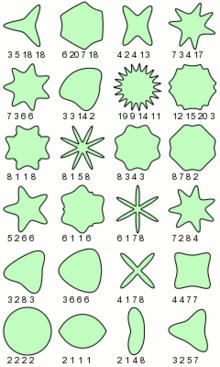
Декілька прикладів кривих, що описуються суперформулою для різних значень m, n₁, n₂ і n₃ за умови a=b=1

Й.Джиліс припустив, що формула може бути використана для опису багатьох складних форм і кривих, які зустрічаються в природі[1].

Запис рівняння

У полярних координатах, для $r$ радіуса і кута $\varphi$ , суперформула має вигляд:

$r\left(\varphi \right)=\left[\left|{\frac {\cos \left({\frac {m\varphi }{4}}\right)}{a}}\right|^{n_{2}}+\left|{\frac {\sin \left({\frac {m\varphi }{4}}\right)}{b}}\right|^{n_{3}}\right]^{-{\frac {1}{n_{1}}}},$

де $m$ — характеризує число фрагметів, що повторюються;

n_{1}

,

n_{2}

,

n_{3}

— параметри, що визначають форму;

a

,

b

— габарити (величини півосей).

Графіки

Інші приклади кривих, побудованих за супреформулою для вказаних m, n₁, n₂ і n₃ при a = b = 1

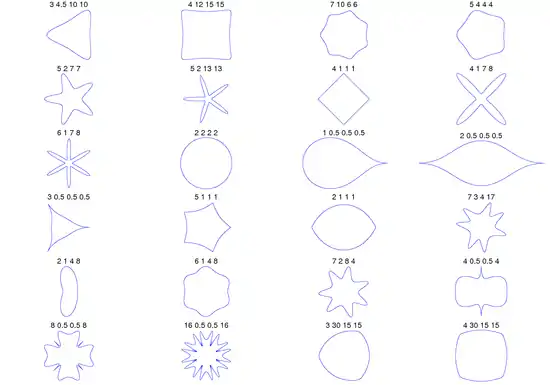
Програмні реалізації побудови кривих

GNU Octave

Програма для генерування кривих на основі суперформули мовою програмування GNU Octave:

  function sf2d(n,a)
    u=[0:.001:2*pi];
    raux=abs(1/a(1).*abs(cos(n(1)*u/4))).^n(3)+abs(1/a(2).*abs(sin(n(1)*u/4))).^n(4);
    r=abs(raux).^(-1/n(2));
    x=r.*cos(u);
    y=r.*sin(u);
    plot(x,y);
  end

PHP script

PHP-скрипт для генерування таких фігур:

<?php
	header("Content-type: image/png");
	set_time_limit(120);
	$img = imagecreatetruecolor(800, 800);
	$black = imagecolorallocate($img, 0, 0, 0);
	imagefilledrectangle($img, 0, 0, 800, 800, $black);

	$center = 400;
	$PI = 2 * pi();

	$a = 1;
	$b = 1;
	$m = 12;
	$n1 = 5;
	$n2 = 6;
	$n3 = 48;

	for($f = 0; $f <= $PI; $f += 0.0001) {
		$r= pow((pow(abs(cos($m*$f/4)/$a),$n2) + pow(abs(sin($m*$f/4)/$b), $n3)), -(1/$n1));
		$x = $center + $r * cos ($f) * 100;
		$y = $center + $r * sin ($f) * 100;
		$col = imagecolorallocate($img, 255, 255, 255);
		imagesetpixel($img, $x, $y, $col);
	}

	print imagepng($img);
	imagedestroy($img);
?>

Узагальнення на більшу кількість вимірів

Рівняння

Є можливим розширення суперформули до 3, 4, чи n вимірів, у сферичній системі координат. Наприклад тривимірне параметричне задання поверхні отримується перемноженням двох суперформул r₁ and r₂. Геометричне місце точок відповідної поверхні може бути задане співвідношеннями:

x\,=\,r_{1}(\theta )\cos(\theta )r_{2}(\phi )\cos(\phi )

y\,=\,r_{1}(\theta )\sin(\theta )r_{2}(\phi )\cos(\phi )

z\,=\,r_{2}(\phi )\sin(\phi ),

де $\phi$ змінюється у межах від -π/2 до π/2 (широта) і θ в діапазоні між -π та π (довгота).

Графічні побудови

Тривимірна суперформула для a = b = 1:

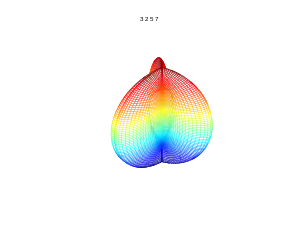m=3, n₁=2, n₂=5, n₃=7
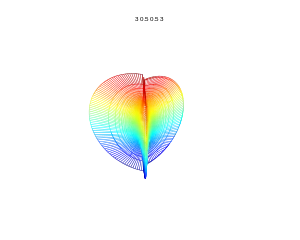m=3, n₁=5, n₂=5, n₃=5
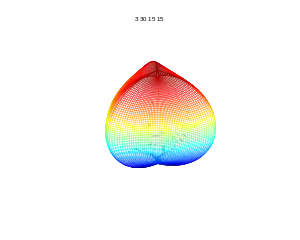m=3, n₁=30, n₂=15, n₃=15
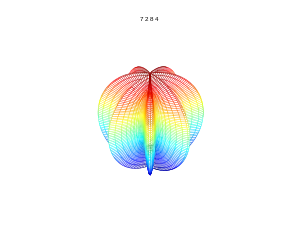m=7, n₁=2, n₂=8, n₃=4
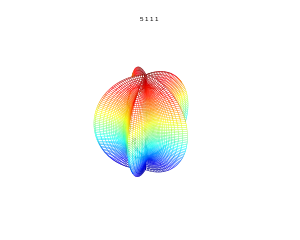m=5, n₁=1, n₂=1, n₃=1
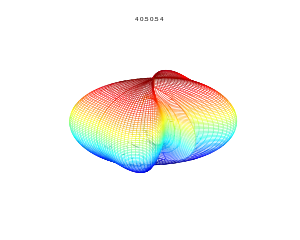m=4, n₁=0.5, n₂=0.5, n₃=4
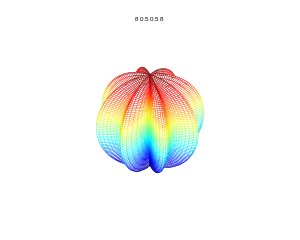m=8, n₁=0.5, n₂=0.5, n₃=8
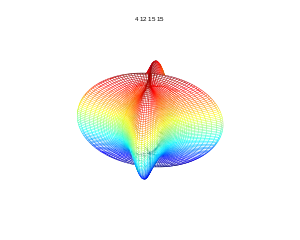m=4, n₁=12, n₂=15, n₃=15

Програма у GNU Octave

Показані вище фігури згенеровано наступним скриптом GNU Octave:

 function sf3d(n, a)
  u=[-pi:.05:pi];
  v=[-pi/2:.05:pi/2];
  nu=length(u);
  nv=length(v);
    for i=1:nu
    for j=1:nv
      raux1=abs(1/a(1)*abs(cos(n(1).*u(i)/4))).^n(3)+abs(1/a(2)*abs(sin(n(1)*u(i)/4))).^n(4);
      r1=abs(raux1).^(-1/n(2));
      raux2=abs(1/a(1)*abs(cos(n(1)*v(j)/4))).^n(3)+abs(1/a(2)*abs(sin(n(1)*v(j)/4))).^n(4);
      r2=abs(raux2).^(-1/n(2));
      x(i,j)=r1*cos(u(i))*r2*cos(v(j));
      y(i,j)=r1*sin(u(i))*r2*cos(v(j));
      z(i,j)=r2*sin(v(j));
    endfor;
  endfor;
  mesh(x,y,z);
 endfunction;

Див. також

Супереліпс

Примітки

Gielis Johan A generic geometric transformation that unifies a wide range of natural and abstract shapes American Journal of Botany 90 (3): 333–338, 2003. ISSN 0002-9122

Посилання

Some Experiments on Fitting of Gielis Curves by Simulated Annealing and Particle Swarm Methods of Global Optimization (англ.)
Least Squares Fitting of Chacón-Gielis Curves By the Particle Swarm Method of Optimization (англ.)
Superformula 2D Plotter & SVG Generator (англ.)
Interactive example using JSXGraph (англ.)
3D Superdupershape Explorer using Processing (англ.)
Interactive 3D Superformula plotter using Processing (with code) (англ.)
SuperShaper: An OpenCL accelerated 3D SuperShape generator with shader based visualisation (OpenGL3) (англ.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Gielis Johan A generic geometric transformation that unifies a wide range of natural and abstract shapes American Journal of Botany 90 (3): 333–338, 2003. ISSN 0002-9122