Широта

	Карта Землі
Довгота (λ)
	Лінії довготи на цій проєкції виглядають викривленими та у вертикальними, але насправді вони є половинами великих кіл.
Широта (φ)
	Лінії широти в цій проєкції виглядають прямими та горизонтальними, але насправді вони є колами різних радіусів. Всі точки з однією широтою утворюють паралель.
Екватор ділить планету на Північну та Південну півкулі. Він лежить на широті 0°.

Широта́ (лат. Latitudo geographica) — одна з координат у ряді систем сферичних координат, що визначають розташування точок на земній поверхні (див. Географічні координати, Координати в геодезії), на небесній сфері (див. Системи небесних координат), на поверхні Сонця, планет та інших небесних тіл (геліоцентричні координати, планетографічні координати тощо).

Для Землі залежно від способу визначення розрізняють широту астрономічну та широту геодезичну.

Астрономічна широта φ точки на поверхні Землі дорівнює куту між прямовисною лінією (нормаллю до геоїда) у цій точці й площиною земного екватора; вона дорівнює також висоті полюса світу над обрієм і вважається додатною в північній півкулі та від'ємною в південній. Широта точок земного екватора становить 0°, Північного полюса +90°, Південного −90°. Лінії з рівними значеннями φ є паралелями.

На відміну від астрономічної широти, визначеної з астрономічних спостережень, геодезична широта обчислюється на основі вимірів на земній поверхні, наприклад методом триангуляції, між визначеним і деяким вихідним пунктом. Геодезична широта дорівнює куту, утвореному лінією — нормаллю, що проходить через задану точку до прийнятого референц-еліпсоїда й площиною його екватора.

Геоцентрична широта φ´ дорівнює куту між радіусом, проведеним із центра земного еліпсоїда в дану точку, і площиною екватора.

Між астрономічною та геоцентричною широтою існує залежність: tg φ´ =(b/a)² tgφ, де а — велика та b — мала півосі земного еліпсоїда. Найбільшого значення різниця Δφ = φ´ досягає при φ = 45° (Δφ≈ 11'5), а на екваторі й полюсах Δφ = 0.

У геодезії вживають також приведену широту u, значення якої лежать між φ та φ´ і визначаються формулою tg u = (b/a) tg φ.

Широта на сфері

Назви особливих широт Землі

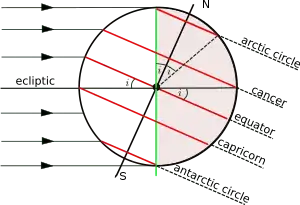
Орієнтація Землі під час зимового сонцестояння.

Крім екватора, спеціальні назви мають ще чотири паралелі:

Полярне коло	66° 34′ (66,57°) N
Тропік Рака	23° 26′ (23,43°) N
Тропік Козорога	23° 26′ (23,43°) S
Південне полярне коло	66° 34′ (66,57°) S

Площина земної орбіти називається також площиною екліптики. Площина, перпендикулярна осі обертання Землі, називається екваторіальною площиною. Кут між площинами екліптики і екватору називається нахилом екліптики і позначений на малюнку літерою $i$ . Поточне значення цього кута — 23°26'21". Його також називають осьовим нахилом Землі, оскільки він дорівнює куту між віссю обертання і нормаллю до площини екліптики. Вісь обертання повільно коливається і змінює з часом свій нахил; тому значення можна наводити лише для певного моменту (наприклад, поточної епохи). Детальніше ця варіація осі обертання з часом описана в статті про нахил осі обертання.

На малюнку показаний поперечний переріз здовж площини, яка перпендикулярна екліптиці і проходить через центр Землі, а Сонце перебуває в зеніті над тропіком Козерога в час зимового сонцестояння. В південних полярних широтах, що розташовані нижче полярного кола, буде день, в той час як в північних полярних широтах, що вище полярного кола, буде ніч. Ситуація зміниться на протилежну в час літнього сонцестояння, коли сонце перебуває в зеніті над тропіком Рака. Широти тропіків дорівнюють $\pmi$ , а полярних кіл — $\pm(90°-i)$ , де $i$ — нахил осі обертання Землі. Сонце може спостерігатися в зеніті тільки на тих широтах, що містяться між двома тропіками.

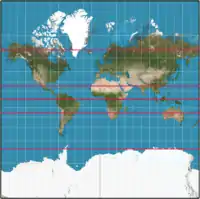
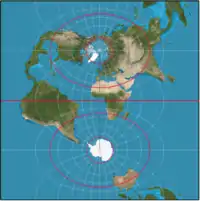
При побудові картографічних проєкцій не існує одного універсального правила, щодо того як мають виглядати меридіани і паралелі. На прикладі нижче показано як перелічені паралелі (червоні лінії) виглядатимуть за загальновживаних проєкції Меркатора і поперечній проєкції Меркатора. На першій проєкції паралелі горизонтальні, а меридіани вертикальні, а на останній і паралелі і меридіани не виглядають горизонтальними і вертикальними, а обидва є складними кривими.

	Звичайна проєкція Меркатора		Поперечна проєкція Меркатора
		\

Відстань здовж меридіану на сфері

На сфері нормаль проходить через її центр, і таким чином широта ( $φ$ ) буде дорівнювати куту, що перебуває в центрі сфери і опирається на дугу меридіана від екватора до даної точки на сфері. Якщо дугу меридіана позначити як $m (φ)$ тоді

m(\phi )={\frac {\pi }{180^{\circ }}}R\phi _{\mathrm {degrees} }=R\phi _{\mathrm {radians} }

де $R$ позначає середній радіус Землі. Це значення $R$ становить 6371 км. Більшої точності для $R$ мати не потрібно, оскільки більшу точність отриманого результату можна досягти лише при використанні еліпсоїдної моделі Землі. При такому значенні $R$ довжина по меридіану, що відповідає 1 градусу широти на сфері становить 111,2 км. Довжина 1 хвилини широти на сфері становить 1,853 км, ця відстань використовується для визначення морської милі.

Широта на еліпсоїді

Еліпсоїди

У 1687 Ісаак Ньютон опублікував роботу «Математичні начала натуральної філософії», де він довів, що рідкі само-гравітаційні тіла, які обертаються в умовах рівноваги, приймають форму сплюсненого еліпсоїда.[1] (В цій статті використовується термін «еліпсоїд» замість більш старшого терміна «сфероїд»). У 18-му столітті результат Ньютона був підтверджений геодезичними вимірюваннями. (Див. дуги меридіана.) Сплюснутий еліпсоїд є тривимірною поверхнею, що утворюється шляхом обертання еліпса навколо своєї малої осі. Термін «сплюснутий еліпсоїд обертання» скорочують до одного слова «еліпсоїд». (Еліпсоїди, які не мають осі симетрії, називають триосьовими.)

В історії геодезії використовувалися різні референц-еліпсоїди. До появи супутників вони створювалися аби дату найкращу наближеність до геоїда в обмеженій області дослідження, але з появою GPS стали зазвичай використовувати еліпсоїди, центри яких розміщені в центрі маси Землі (наприклад, WGS84), а мала вісь збігається з віссю обертання Землі. Ці геоцентричні еліпсоїди, як правило, розходяться з геоїдом не більше ніж на 100 м. Оскільки широта визначається відповідно до еліпсоїда, місцерозташування в даній точці буде різним на кожному еліпсоїді: неможливо точно вказати широту і довготу географічного об'єкта без указання еліпсоїда, що використовується. Багато з карт, які підтримуються національними організаціями, можуть використовувати старі версії еліпсоїда, тому необхідно знати, як перерахувати значення широти і довготи при переході з одного еліпсоїда на інший. GPS-приймачі і телефони часто включають програмне забезпечення для виконання розрахунків з перетворень різних референцних систем, які дозволяють перерахувати WGS84 у координати з використанням місцевого референц-еліпсоїда і пов'язаної з ним сітки.

Джерела інформації

Большая советская энциклопедия (БСЭ). (рос.)

Посилання

Географічні координати // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.
http://avstop.com/ac/fig8-2.jpg

Примітки

Newton, Isaac. Book III Proposition XIX Problem III. Philosophiæ Naturalis Principia Mathematica (translated into English by Andrew Motte). с. 407.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[newton-1] Newton, Isaac. Book III Proposition XIX Problem III. Philosophiæ Naturalis Principia Mathematica (translated into English by Andrew Motte). с. 407.