Теорема Вівіані

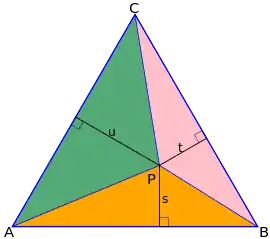
Теорему можна довести шляхом порівняння площ трикутників. Нехай ${\displaystyle \triangle ABC}$ — рівносторонній трикутник, у якому ${\displaystyle h}$ — це висота, і ${\displaystyle a}$ — довжина кожної із сторін. Точка ${\displaystyle P}$ обирається довільно всередині трикутника, і тоді ${\displaystyle t}$, ${\displaystyle u}$, ${\displaystyle s}$ — відстані від точки ${\displaystyle P}$ до сторін трикутника. Тоді площа ${\displaystyle \triangle ABC}$ може бути визначена таким способом:

${\displaystyle S_{\triangle ABC}=S_{\triangle ABP}+S_{\triangle ACP}+S_{\triangle BCP}}$,

Звідки випливає співвідношення:

${\displaystyle {\frac {ah}{2}}={\frac {at}{2}}+{\frac {au}{2}}+{\frac {as}{2}}}$,

тобто:

${\displaystyle h=t+u+s}$,

що і потрібно було довести.

Діаграма займистості метану

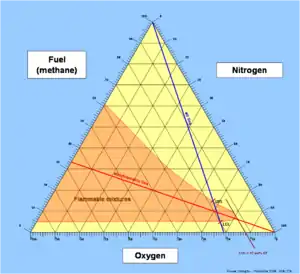
Теорема Вівіані дозволяє отримувати координати точок на трикомпонентних діаграмах шляхом проведення ліній, паралельних до сторін рівностороннього трикутника. Зокрема так можна будувати діаграми займистості.

У загальнішому випадку, вона дозволяє задавати координати на правильному симплексі.

• Weisstein, Eric W. Viviani's Theorem(англ.) на сайті Wolfram MathWorld.
• Li Zhou, Viviani Polytopes and Fermat Points
• Viviani's Theorem: What is it? at Cut the knot.
• Viviani's Theorem by Jay Warendorff, the Wolfram Demonstrations Project.