Теорема Ейлера про чотирикутник

Теорема Ейлера про чотирикутник (також закон Ейлера для чотирикутників) — теорема планіметрії, названа на честь Леонарда Ейлера, яка описує співвідношення між сторонами опуклого чотирикутника і його діагоналями. Теорема є узагальненням тотожності паралелограма, яку, в свою чергу, можна розглядати як узагальнення теореми Піфагора; тому іноді використовують назву теорема Ейлера — Піфагора.

a^{2}+b^{2}+c^{2}+d^{2}=e^{2}+f^{2}+4g^{2}

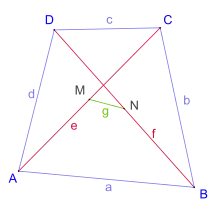
Теорема і окремі випадки

Для опуклого чотирикутника зі сторонами $a,b,c,d$ і діагоналями $e$ і $f$ , середини яких з'єднані відрізком $g$ , виконується рівність:

a^{2}+b^{2}+c^{2}+d^{2}=e^{2}+f^{2}+4g^{2}

Якщо чотирикутник є паралелограмом, то середні точки діагоналей збігаються і довжина відрізка $g$ , що з'єднує їх, дорівнює 0. Крім того, у паралелограма довжини паралельних сторін рівні, отже, в такому випадку теорема Ейлера зводиться до формули:

2a^{2}+2b^{2}=e^{2}+f^{2}

яку називають тотожністю паралелограма.

Якщо чотирикутник є прямокутником, то рівність ще спрощується, оскільки тепер дві діагоналі рівні:

2a^{2}+2b^{2}=2e^{2}

Ділення на 2 дає теорему Ейлера — Піфагора:

a^{2}+b^{2}=e^{2}

Іншими словами: для прямокутника відношення сторін чотирикутника і його діагоналей описує теорема Піфагора[1].

Альтернативні формулювання та розширення

Теорема Ейлера для паралелограма

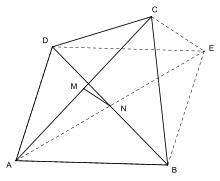
Ейлер вивів описану вище теорему як наслідок іншої теореми, яка, з одного боку, менш елегантна, оскільки вимагає додавання ще однієї точки, але, з іншого боку, дає більше розуміння властивостей чотирикутника.

Для заданого опуклого чотирикутника $ABCD$ Ейлер увів додаткову точку $E$ , таку, що $ABED$ утворює паралелограм; тоді виконується така рівність:

|AB|^{2}+|BC|^{2}+|CD|^{2}+|AD|^{2}=|AC|^{2}+|BD|^{2}+|CE|^{2}

Відстань $|CE|$ між додатковою точкою $E$ і точкою $C$ чотирикутника, відповідає відрізку, який не є частиною паралелограма. Довжину цього відрізка можна розглядати як міру відмінності розглянутого чотирикутника від паралелограма, або, іншими словами, як міру правильності члена $|CE|^{2}$ у початковій рівності тотожності паралелограма[2].

Оскільки точка $M$ є серединою відрізка $AC$ , то отримуємо ${\tfrac {|AC|}{|AM|}}=2$ . Точка $N$ є серединою відрізка $BD$ , і вона також є серединою відрізка $AE$ , оскільки $AE$ і $BD$ є діагоналями паралелограма $ABED$ . Звідси отримуємо ${\tfrac {|AE|}{|AN|}}=2$ , і, отже, ${\tfrac {|AC|}{|AM|}}={\tfrac {|AE|}{|AN|}}$ . Із теореми Фалеса (і оберненої) випливає, що $CE$ і $NM$ паралельні. Тоді $|CE|^{2}=(2|NM|)^{2}=4|NM|^{2}$ , звідки й випливає теорема Ейлера[2].

Теорему Ейлера можна розширити на множину чотирикутників, яка включає перетинні і непланарні. Вона виконується для так званих узагальнених чотирикутників, які складаються з чотирьох довільних точок у просторі $\mathbb {R} ^{n}$ , пов'язаних ребрами з утворенням циклічного графу[3].

Примітки

Debnath, 2010, с. 105–107.
Haunsperger, Kennedy, 2006, с. 137–139.
Kandall, 2002, с. 403–404.

Література

Deanna Haunsperger, Stephen Kennedy. The Edge of the Universe: Celebrating Ten Years of Math Horizons. — MAA, 2006. — С. 137–139. — ISBN 9780883855553.
Lokenath Debnath. The Legacy of Leonhard Euler: A Tricentennial Tribute. — World Scientific, 2010. — С. 105–107. — ISBN 9781848165267.
C. Edward Sandifer. How Euler Did It. — MAA, 2007. — С. 33–36. — ISBN 9780883855638.
Geoffrey A. Kandall. Euler's Theorem for Generalized Quadrilaterals // The College Mathematics Journal. — 2002. — Т. 33, № 5 (Nov.). — С. 403–404.
Dietmar Herrmann. Die antike Mathematik: Eine Geschichte der griechischen Mathematik, ihrer Probleme und Lösungen. — Springer, 2013. — С. 418. — ISBN 9783642376122.

Посилання

Weisstein, Eric W. Чотирикутник(англ.) на сайті Wolfram MathWorld.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[FOOTNOTEDebnath2010105–107-1] Debnath, 2010, с. 105–107.

[FOOTNOTEHaunsperger,_Kennedy2006137–139-2] Haunsperger, Kennedy, 2006, с. 137–139.

[FOOTNOTEKandall2002403–404-3] Kandall, 2002, с. 403–404.