Прямокутник

Опуклий чотирикутник буде вважатися прямокутником тоді й лише тоді коли виконується принаймні одне із наступних тверджень:[4][5]

• паралелограм із принаймні одним прямим кутом,
• паралелограм, діагоналі якого мають однакову довжину,
• паралелограм ABCD в якому трикутники ABD і DCA є конгруентними,
• рівнокутний чотирикутник,
• чотирикутник із чотирма прямими кутами.

Основні властивості прямокутника[6]:

• Діагоналі прямокутника рівні.
• Діагоналі прямокутника перетинаються і точкою перетину діляться навпіл.
• Діагоналі прямокутника ділять його на два рівні трикутники.
• Висоти прямокутника є одночасно і його сторонами.
• Навколо будь-якого прямокутника можна описати коло, причому діагональ прямокутника дорівнює діаметру даного кола.
• Квадрат діагоналі прямокутника дорівнює сумі квадратів двох його не протилежних сторін.

Прямокутник є плоскою геометричною фігурою, його аналогом у тривимірному просторі є прямокутний паралелепіпед.

Формула для визначення периметра прямокутника

Якщо прямокутник має довжину ${\displaystyle \ell }$ і ширину ${\displaystyle w}$

• він матиме площу ${\displaystyle A=\ell w\,}$,
• він матиме периметр ${\displaystyle P=2\ell +2w=2(\ell +w)\,}$,
• довжина кожної діагоналі дорівнюватиме ${\displaystyle d={\sqrt {\ell ^{2}+w^{2}}}}$,
• якщо ${\displaystyle \ell =w\,}$, прямокутник є квадратом.

Ізопериметрична нерівність для прямокутників доводить, що серед усіх прямокутників із заданим периметром, квадрат матиме найбільшу площу.

Лінії проведені через середні точки сторін будь-якого чотирикутника із перпендикулярними діагоналями утворюють прямокутник.

Паралелограм із рівними за довжиною діагоналями є прямокутником.

Японська теорема про вписаний в коло чотирикутник[7] говорить, що центри вписаних кіл чотирьох трикутників, які задані вписаним у інше коло чотирикутником утворюють прямокутник.

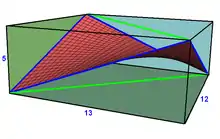
Теорема про Британський прапор стверджує, що якщо вершини прямокутника позначені як A, B, C, і D, для будь-якої точки P в тій самій площині в середині прямокутника буде виконуватися рівність:[8]

${\displaystyle \displaystyle (AP)^{2}+(CP)^{2}=(BP)^{2}+(DP)^{2}.}$

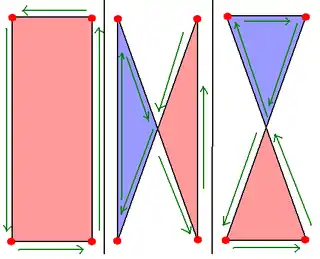
Схрещений прямокутник (такий, що перетинає сам себе) складається із двох протилежних сторін звичайного прямокутника і двох діагоналей. Схрещений прямокутник, так само, є різновидом схрещеного чотирикутника. Він має той самий порядок вершин. Він представлений двома ідентичними трикутниками із спільною вершиною, але геометричний перетин не розглядається як вершина.

Схрещений чотирикутник іноді асоціюють із краваткою-метеликом або формою метелика. Тривимірну прямокутну каркасну конструкцію із дроту можна скрутити таким чином, що вона прийме форму метелика. Схрещений прямокутник іноді називають "кутовою вісімкою".

Внутрішня частина схрещеного прямокутника може мати полігональну густину, що дорівнює ±1 для кожного трикутника, в залежності від того як закручено цей прямокутник, за годинниковою стрілкою чи проти.

Схрещений прямокутник не є рівнокутним. Сума його внутрішніх кутів (двох гострих і двох розгорнутих кутів), як і в будь-якого схрещеного прямокутника, дорівнює 720°.[9]

Прямокутник і схрещений прямокутник є чотирикутниками, що мають наступні спільні властивості:

• Протилежні сторони мають однакову довжину.
• Дві діагоналі мають однакову довжину.
• Він має дві прямі, що визначають дзеркальну симетрію і обертову симетрію порядку 2 (через 180°).

Сідловий прямокутник має 4 не планарні вершини і утворений частковим усіканням із вершин прямокутного паралелепіпеда, що є єдиною внутрішньою мінімальною поверхнею, яка визначається як лінійна комбінація чотирьох вершин. На малюнку показано синім показано 4 ребра прямокутника, і дві діагоналі зеленим, всі вони є діагоналями прямокутних граней паралелепіпеда.

У сферичній геометрії, сферичним прямокутником називають фігуру із чотирма ребрами, які є дугами великого кола, які утворюють однакові кути більші за 90°. Протилежні дуги мають однакову довжину. Сферична геометрія є найпростішою формою еліптичної геометрії. Поверхня сфери в Евклідовій геометрії є не Евклідовою поверхнею в розумінні еліптичної геометрії.

В еліптичній геометрії, еліптичним прямокутником є фігура у еліптичній площині, чотири ребра якої є еліптичними дугами, які також утворюють однакові кути більші за 90°. Протилежні дуги мають однакову довжину.

В гіперболічній геометрії, гіперболічним прямокутником є фігура в гіперболічній площині, чотири ребра якої є гіперболічними дугами, які утворюють між собою однакові кути менші за 90°. Протилежні дуги мають однакову довжину.

• Паралелограм
• Чотирикутник
• Трапеція
• Квадрат
• Прямокутний паралелепіпед