Теорема Косніти
Теорема Косніти — це властивість деяких кіл, пов'язаних з довільним трикутником.
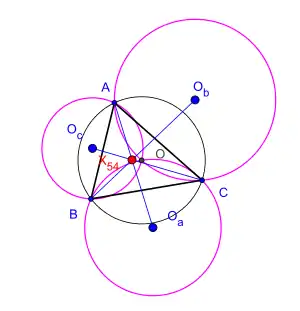
Точка Косніти x(54) трикутника ABC
Нехай — довільний трикутник, — центр його описаного кола, а — центри описаних кіл трьох трикутників , і відповідно. Теорема стверджує, що три прямих , і перетинаються в одній точці[1]. Цей факт встановив румунський математик Цезар Косніта (Cezar Coşniţă, 1910—1962)[2].
Точка, в якій прямі перетинаються, відома як точка Косніти трикутника (назву дав Рігбі в 1997). Точка є ізогонально спряженою центру дев'яти точок[3][4]. Точка має позначення поміж чудових точок трикутника в списку Кімберлінга[5]. Теорема є окремим випадком теореми Дао про 6 центрів описаних кіл для вписаного шестикутника[6][7][8][9].
Властивості
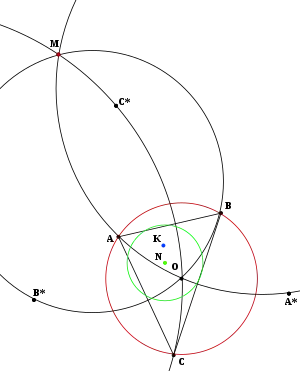
Трикутник T з вершинами A, B і C; O — центр описаного кола (червоне).
A*, B* і C* — точки, симетричні точкам A, B і C відносно протилежної сторони.
M — точка перетину кіл Масельмана.
Зелене коло — коло дев'яти точок, N — його центр.
K — точка Косніти.
A*, B* і C* — точки, симетричні точкам A, B і C відносно протилежної сторони.
M — точка перетину кіл Масельмана.
Зелене коло — коло дев'яти точок, N — його центр.
K — точка Косніти.
- Точка Косніти K тісно пов'язана з точкою M Масельмана (з точкою перетину кіл Масельмана). Див. рис. і теорему Масельмана. Точка Масельмана є точкою інверсії точки Косніти відносно кола, описаного навколо трикутника .
Примітки
- Weisstein, Eric W. Теорема Косніти(англ.) на сайті Wolfram MathWorld.
- Ion Pătraşcu (2010), A generalization of Kosnita's theorem (рум.)
- Grinberg, 2003, с. 105–111.
- Rigby, 1997, с. 156-158.
- Clark Kimberling (2014), Encyclopedia of Triangle Centers, section X(54) = Kosnita Point. Accessed on 2014-10-08
- Dergiades, 2014, с. 243–246.
- Cohl, 2014, с. 261–264.
- Duong, 2016, с. 25-39.
- X(3649) = KS(INTOUCH TRIANGLE)
Література
- John Rigby. Brief notes on some forgotten geometrical theorems // Mathematics and Informatics Quarterly. — 1997. — Т. 7 (28 жовтня). — С. 156-158. (как процитировано у Кимберлинга).
- Darij Grinberg. On the Kosnita Point and the Reflection Triangle // Forum Geometricorum. — 2003. — Т. 3 (28 жовтня). — С. 105–111.
- Nikolaos Dergiades. Dao’s Theorem on Six Circumcenters associated with a Cyclic Hexagon // Forum Geometricorum. — 2014. — Т. 14 (28 жовтня). — С. 243–246. — ISSN 1534-1178.
- Telv Cohl. A purely synthetic proof of Dao's theorem on six circumcenters associated with a cyclic hexagon // Forum Geometricorum. — 2014. — Т. 14 (28 жовтня). — С. 261–264. — ISSN 1534-1178.
- Ngo Quang Duong. Some problems around the Dao's theorem on six circumcenters associated with a cyclic hexagon configuration // International Journal of Computer Discovered Mathematics. — 2016. — Т. 1 (28 жовтня). — С. 25-39. — ISSN 2367-7775.
Посилання
- Weisstein, Eric W. Теорема Косніти(англ.) на сайті Wolfram MathWorld.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.