Теорема про три геодезичні

Тривісний еліпсоїд та його три геодезичні

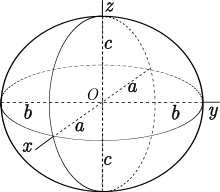
Виникнення теореми пов'язане із математикою навігації в океані, де поверхня Землі може бути точно змодельована за допомогою еліпсоїда, а також у зв'язку з вивченням геодезичних на еліпсоїді. Зокрема, тривісний еліпсоїд має тільки три прості замкнуті геодезичні що є його екваторами.[3] У 1905 році Анрі Пуанкаре висловив гіпотезу, що будь-яка гладка поверхня, що топологічно еквівалентна сфері аналогічним чином містить щонайменше три прості замкнені геодезичні[4], а в 1929 р Люстерник і Шнирельман опублікували доказ гіпотези в якому пізніше були знайдені недоліки.[5] В одному з доказів цієї гіпотези розглядаються гомології простору гладких кривих на сфері та укорочуючий потік з метою знайдення простої замкненої геодезичної, що представляє кожен з трьох нетривіальних класів гомології цього простору.[2]

Більш того, обов'язково існують три прості замкнені геодезичні, довжина яких найбільш пропорційна діаметру поверхні. [6]

Кількість замкнених геодезичних довжини щонайбільше L на гладкій топологічній сфері зростає пропорційно L/log L, але не можна гарантувати, що такі геодезичні будуть простими. [7]

На компактних гіперболічних ріманових поверхнях існує нескінченно багато простих замкнених геодезичних, але тільки скінченна кількість із заданою довжиною буде обмежена. Вони аналітично задаються за допомогою дзета-функції Сельберга. Оцінки швидкості зростання кількості простих замкнених геодезичних, як функції їх довжини, досліджувала Мар'ям Мірзахані.[8]

Можна визначити геодезичну на деякій поверхні, що не є всюди гладкою, така, як опуклий багатогранник. Однак, деякі многогранники мають прості замкнені геодезичні, (наприклад тетраедр та рівнограний тетраедр мають нескінченно багато простих замкнених геодезичних)[9][10] інші не мають. Зокрема, проста замкнена геодезична на опуклому багатограннику обов'язково буде ділити навпіл сумарний дефект вершин, та для майже всіх багатограників це не буде вірно.[3][9]

Проте, теорему про три геодезичні можна поширити на випадок квазігеодезичних на опуклому багатогранику. Тобто, будь-який багатограник має хоча б три прості замкнені квазігеодезичні, що можна довести шляхом наближення багатограника до гладкої поверхні після чого застосувати теорему про три геодезичні.[11] Можливість побудови квазігеодезичної на опуклому багатогранику за поліноміальний час є відкритим питанням.